五年级下册数学教案 长方体和正方体的体积 北京版 (1)

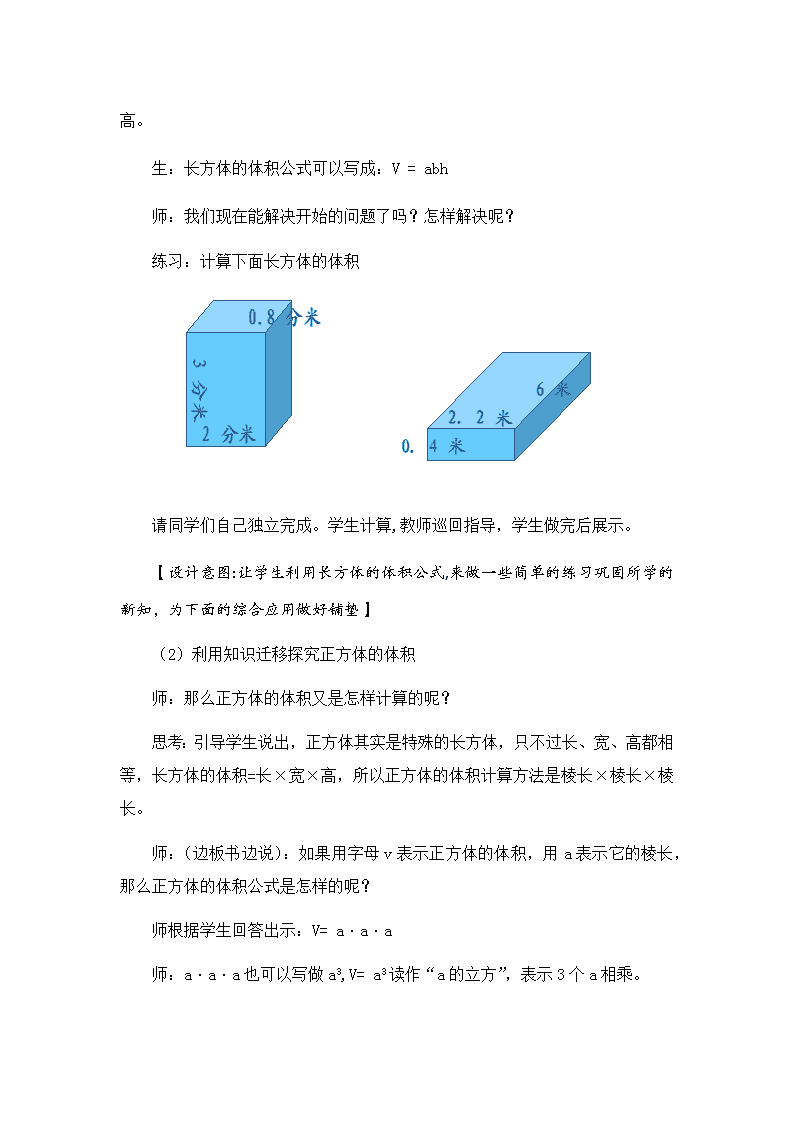
五年级下册数学教案 长方体和正方体的体积 北京版 (1)

‎《长方体和正方体的体积》教学设计 一、教学目标 ‎1. 结合具体情境和实践活动,探索并掌握长方体、正方体的体积的计算方法,能正确计算长方体、正方体的体积。‎ ‎2. 通过“猜想—验证”的过程,获取数学活动经验。‎ ‎3. 在观察、操作、探索的过程中,提高动手操作能力,进一步发展空间观念,并解决一些简单的实际问题。‎ 二、教学重难点 重点:理解长方体和正方体的体积公式的推导过程,掌握计算方法。‎ 难点:理解长方体和正方体的体积公式的推导过程。‎ 三、教学准备 教具准备：教学课件 学具准备：每各小组12个边长1立方厘米的小木块 四、教学过程 ‎1、情景导入 师：出示幻灯片，那个体积大？‎ 生：黄色的长方体体积大？‎ 师：出示幻灯片，那个体积大？‎ 生：看不出来？ ‎ 师：看不出来就要进行计算，用数据说话，我们今天要共同解决的就是怎样计算它的体积。（板书课题：长方体和正方体的体积）‎ ‎2、探究体验、学习新知 ‎（1）探究长方体的体积公式。‎ 师：同学们那同学们大胆猜想一下，长方体的体积和什么有关呢？有怎样的关系？‎ 生：长方体的体积和它的长、宽、高。‎ 师：取出12个体积是1立方厘米的正方体，摆出不同形状的长方体。 ‎ 小组合作要求： ‎ ‎1）两个同学摆长方体，两个同学观察摆好的长方体，两个同学做记录完成表格。 ‎ ‎2）每个小组尽可能多的摆出不同的长方体。 ‎ ‎3）你发现了什么？‎ 把小组内摆法不同的长方体的相关数据填入下表：‎ 每排 个数 排数 层数 长（cm）‎ 宽（cm）‎ 高（cm）‎ 小正方体的数量 长方体的体积（cm3）‎ 教师将学生汇报的各种摆法的数据逐一填入表中。‎ 师：归纳体积计算方法。长方体的体积=长×宽×高。‎ 师：如果用字母V表示长方体的体积，用a、b、h分别表示长方体的长、宽、高。‎ 生：长方体的体积公式可以写成：V = abh ‎ 师：我们现在能解决开始的问题了吗？怎样解决呢？‎ 练习：计算下面长方体的体积 ‎ ‎ 请同学们自己独立完成。学生计算,教师巡回指导，学生做完后展示。‎ ‎【设计意图:让学生利用长方体的体积公式,来做一些简单的练习巩固所学的新知，为下面的综合应用做好铺垫】‎ ‎（2）利用知识迁移探究正方体的体积 师：那么正方体的体积又是怎样计算的呢？ ‎ 思考：引导学生说出，正方体其实是特殊的长方体，只不过长、宽、高都相等，长方体的体积=长×宽×高，所以正方体的体积计算方法是棱长×棱长×棱长。‎ 师：（边板书边说）：如果用字母v表示正方体的体积，用a表示它的棱长，那么正方体的体积公式是怎样的呢？‎ 师根据学生回答出示：V= a·a·a 师：a·a·a也可以写做a3,V= a3读作“a的立方”，表示3个a相乘。‎ ‎【设计意图:让学生根据长方体和正方体的关系,来推断正方体的体积的计算公式,使学生感觉新知识不难理解,实现平稳过渡,培养学生的推理能力】‎ 练习：一块正方体的石料，棱长是 6 dm。这块石料的体积是多少立方分米？‎ 请同学们自己独立完成。学生计算,教师巡回指导，学生做完后展示。‎ ‎【设计意图:让学生利用正方体的体积公式,来做简单的练习巩固所学的新知，为下面的综合应用做好铺垫】‎ ‎（3）推导：长方体(或正方体)的体积=底面积×高 师:长方体和正方体的底面的面积叫做底面积。‎ 师:请同学们对比一下长方体正方体的体积公式,看一看与底面积有什么关系?‎ 学生观察对比。‎ 生:通过对比,长方体的体积公式可以写成:长方体的体积=底面积×高。‎ 师:同学们总结得很好,这样我们就得到了长方体和正方体的体积的计算公式:长方体(或正方体)的体积=底面积×高,如果用字母S表示底面积,上面的公式可以写成:V=Sh。‎ 练习：一个长方体的底面边长是2分米，高是10分米，它的体积是多少立方分米？‎ ‎3、综合应用、提升技能 一个长方体水箱，长7分米，宽5分米，水深3分米。把一个铁球浸没在水中，水面升高到5分米。这个铁球的体积是多少立方分米？‎ ‎4、课末总结、梳理提升 这节课我们共同探究了长方体和正方体的体积公式,同学们都积极地动手动脑,总结出了它们的计算公式。‎ 长方体的体积=长×宽×高　　　　　　正方体的体积=棱长×棱长×棱长 V=abh　　　　　　　　　　　　　　　V=a3‎ 长方体(或正方体)的体积=底面积×高 V ＝ sh ‎ ‎5、板书设计 长方体和正方体的体积 长方体的体积=长×宽×高　　　　　正方体的体积=棱长×棱长×棱长 V=abh　　　　　　　　　　　　　　V=a3‎ 长方体(或正方体)的体积=底面积×高 V ＝ sh ‎