五年级数学教案《回顾整理—多边形的面积》

五年级数学教案《回顾整理—多边形的面积》

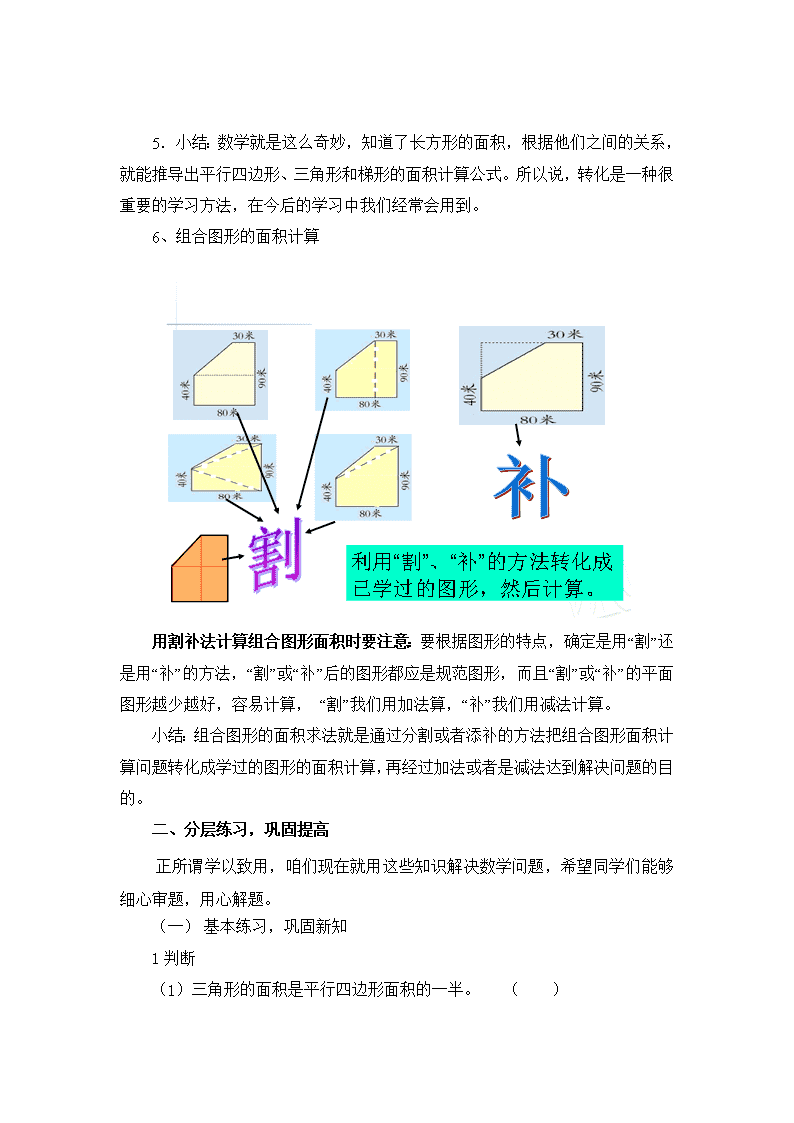
回顾整理——多边形的面积 教学内容： 五年级数学上册第82-84页 综合练习 ‎ 教学目标：‎ ‎ 1．在上节课回顾整理平面图形的特征与相互联系的基础上，自主对平面图形的面积知识进行梳理，体会平面图形面积计算的联系。‎ ‎ 2．能熟练运用面积计算公式计算平面图形的面积，提高灵活应用公式解决问题的能力。 ‎ ‎3．在解决问题的过程中，系统体会转化思想对于解决数学问题的作用,增强空间观念。‎ ‎4．进一步体验图形与生活的联系，感受学习平面图形的价值，提高数学学习的兴趣和学好数学的信心。‎ 教学重点：进一步认识平面图形面积公式的推导过程，提高灵活应用公式解决问题的能力。‎ 教学难点：自主对平面图形的面积的知识进行梳理,体会平面图形面积公式的联系。‎ 教具准备：多媒体课件。‎ 教学过程：‎ 一、问题回顾，再现新知 ‎1．提出问题，小组交流 上节课，我们对平面图形的特征及相互联系进行了回顾整理，这节课，我们进一步梳理平面图形的面积这部分知识。（板书课题：平面图形的面积）回忆一下，正方形、、长方形平行四边形、三角形、梯形的面积计算公式是怎样的？请在小组内交流，你能先用语言叙述，再用字母来表示吗？‎ 小组内交流。‎ ‎2．公式推导，合作整理 提问：这些平面图形的面积计算公式是怎样推导出来的？请各小组借助手中的学具卡片进行演示并说一说。‎ 小组活动，教师参与其中，关注学生能否正确熟练地推导出平行四边形、三角形、梯形的面积公式。‎ ‎3．交流汇报，形成体系 ‎（1）全班交流。学生发表自己的见解，教师重点关注学生能否发现转化的方法，并根据学生回答板书。‎ ‎4．引导提升，体会联系 小结过渡：以上我们对平面图形面积计算公式的推导过程进行了梳理，从中发现在探究一个平面图形面积的计算方法时，都是用拼凑法或割补法把它转化成已学过的图形，利用已学过图形的面积计算公式推导出这种图形的面积计算公式。上节课我们已经发现，平面图形在外观特征上可以互相转化，其实它们的面积计算公式之间还可以转化呢，请看：：‎ ‎5．小结：数学就是这么奇妙，知道了长方形的面积，根据他们之间的关系，就能推导出平行四边形、三角形和梯形的面积计算公式。所以说，转化是一种很重要的学习方法，在今后的学习中我们经常会用到。‎ ‎6、组合图形的面积计算 用割补法计算组合图形面积时要注意：要根据图形的特点，确定是用“割”还是用“补”的方法，“割”或“补”后的图形都应是规范图形，而且“割”或“补”的平面图形越少越好，容易计算， “割”我们用加法算，“补”我们用减法计算。 ‎ 小结：组合图形的面积求法就是通过分割或者添补的方法把组合图形面积计算问题转化成学过的图形的面积计算，再经过加法或者是减法达到解决问题的目的。‎ 二、分层练习，巩固提高 正所谓学以致用，咱们现在就用这些知识解决数学问题，希望同学们能够细心审题，用心解题。‎ （一） 基本练习，巩固新知 ‎1判断 ‎（1）三角形的面积是平行四边形面积的一半。 （ ）‎ ‎（2）两个面积相等的梯形一定能拼成一个平行四边形。（ ）‎ ‎（3）两三角形的高相等，它们的面积就相等。（ ）‎ ‎2综合练习第1‎ 学生先独立测量数据，再计算面积。集体订正，注意单位名称的运用。‎ ‎3综合练习第2题 ‎（1）学生独立完成。‎ ‎（2）集体评议。学生汇报时要求讲清解题方法，如果学生有错误，其他学生纠正、补充。这里要注意计算三角形和梯形面积时是不是忘记除以2，教育学生养成认真仔细的学习习惯。‎ ‎4想一想，画一画。‎ 在下面的方格纸中画出一个平行四边形和一个梯形，使它们的面积和已知三角形的面积相等。（图中的每一个正方形边长1cm）‎ ‎ ‎ ‎（1）学生独立完成，教师巡视了解。‎ ‎（2）组织交流展示。展示学生作业时，让学生说说是怎样确定平行四边形的底和高、梯形的上底、下底和高的，注意学生是否会灵活运用面积计算公式之间的关系来确定各种数据。对于不同的画法，只要合理，均给与肯定。‎ 注意：这里要注意体现平行四边形的面积是等底等高的三角形面积的一半,所以画出的平行四边形可以与三角形等底,但高是三角形高的一半；或者等高,但底是三角形的一半。梯形的画法可以根据平行四边形的底和高，先确定和平行四边形相等的高，然后使梯形的上底与下底的和等于平行四边形上下两底的和。对于这种思路注意进行引导。‎ ‎（二）综合练习，应用新知 ‎1.求x的值 解：设梯形的高为x米。 ‎ ‎（3+7）x ÷2=20‎ ‎ 10x ÷2x2=20x2‎ ‎ 10x=40‎ ‎ 10x ÷10=40 ÷10‎ ‎ X=4‎ 答：梯形的高为4米。 ‎ ‎2.教材综合练习第11题 ‎(1)学生独立解答.‎ ‎(2)全班交流.注意让不同的学生说出求每种花的占地面积选用的多种方法，如计算一串红的占地面积可以用20×10÷2×2计算，也可以用20×10计算，还也可以用40×20÷4进行计算。然后后交流完善各自的算法。‎ ‎3、‎ ‎(三)拓展练习，发展新知 ‎4 教材综合练习第16题 ‎(1)提问：求制作抽风机排气口至少需要多少铁皮，就是求什么？引导学生结合生活经验，理解求制作抽风机排气口至少需要多少铁皮，就是求四个完全相同的梯形的面积。‎ ‎（2）引导学生找出求每个梯形的面积所需要的数据，学生独立进行解答。‎ ‎（3）交流计算结果，注意学生是否注意单位换算。‎ ‎8米 ‎5米 ‎5.补充练习：和爷爷一起算面积 出示问题情境：‎ 星期天，爷爷带心心到 菜园散步，看到菜园旁，长着 一棵郁郁葱葱的大树。她赶忙 拿起纸和笔，画了起来，并把 她估计的数据标上(如图)。她 ‎4米 告诉爷爷，这片地的周长约有36米，请爷爷算一算，这片平行四边形菜地的面积有多少平方米？‎ 爷爷说：“孙女考爷爷，爷爷也得考考你。来，‎ 看爷爷画的鸡圈图：爷爷用了12米长的篱笆靠一面 墙围了一个鸡圈，你能算出这个梯形鸡圈的面积吗？‎ 三、梳理总结，提升认识 ‎1.引导学生梳理总结：同学们，通过这节课的复习，你有哪些收获？‎ 学生自由发言，注意引导学生结合复习内容，对能熟练地计算平面图形的面积、进一步感受数学与生活的密切联系以及数学知识之间的相互转化等进行梳理。‎ ‎2.教师提升：这节课同学们不但能熟练运用平面图形的面积计算方法，解决生活中的数学问题，能清楚地表达自己的思考过程，还进一步感受到转化对于我们学习平面图形的面积所起的重要作用，长方形的面积计算公式是我们学习平面图形面积的基础，转化是则它的灵魂。大家在今后的学习和生活中，还会更多更深入地地用到这种重要的数学思想方法。‎ 板书设计：　‎ 平面图形的面积 转 化 转化 ‎1.设计说明：‎ ‎（1）遵循认知规律，以学生的发展为本。‎ 教学中，通过 “ 温故—— 巩固 —— 提升 ” 等环节，让学生充分动脑、动口、动手、动耳、动眼，在学生自主整理、合作交流中，唤起对所学知识的再认知，由点到面，理清知识脉络，构建知识体系，培养了回顾与反思的能力，通过不同层次的巩固练习，提高学生的学习与运用的能力。同时向学生渗透转化的数学思想，让学生亲身经历了数学的一般研究方法，为学生今后的数学学习和发展打下了基础。‎ ‎（2）在合作中交流，在体验中发展。‎ 在本课教学中，我创设了一种研究探讨的氛围，有意识安排了一次次小组合作交流，让学生在合作中回顾各平面图形面积公式的推导过程；在合作中思考各平面图形面积公式之间的联系等。在合作交流中，将 平面图形面积的孤立的、分散的知识串成线，连成片，结成网，形成知识网络，深刻感受知识之间的内在联系。同时教师把自己放在与学生平等的位置上，与学生融为一体，既分工又合作，这样既能使每个学生都有机会展示自己的思维，获得成功的体验。‎ ‎（3）练习难易适度，在应用中提高。‎ 本节课设计了有层次的练习，从基本的面积计算的题目入手，让学生熟记公式，体会数学公式的简洁美。接着再利用所学知识解决生活问题，训练了学生思维的综合性、多元性、开放性，体现了数学的实用价值及育人功能。最后设计了“和爷爷一起算面积”的拓展练习，让学有余力的学生选做，较好地实现了“不同的人在数学上得到不同的发展”这一教学理念。练习的设计由浅到深、由易到难，难易适度，相得益彰，既对基础知识进行深化，又让学生在练习中灵活运用，提高能力。‎ ‎2.使用建议：在实际教学中，可能因为梳理平面图形的面积用时较长导致练习题无法全部完成，执教教师可以可以根据本班学生特点有选择的进行练习。‎ ‎3.需要破解的问题：本次单元整理组合图形的面积没有涉及到复杂图形面积的计算，只是对简单组合图形面积的计算采用了分割法和添补法计算，对于复杂组合图形的计算是否要将这一知识补充，值得我进一步研究。 ‎