2020年上海市静安区中考数学二模试卷

2020年上海市静安区中考数学二模试卷

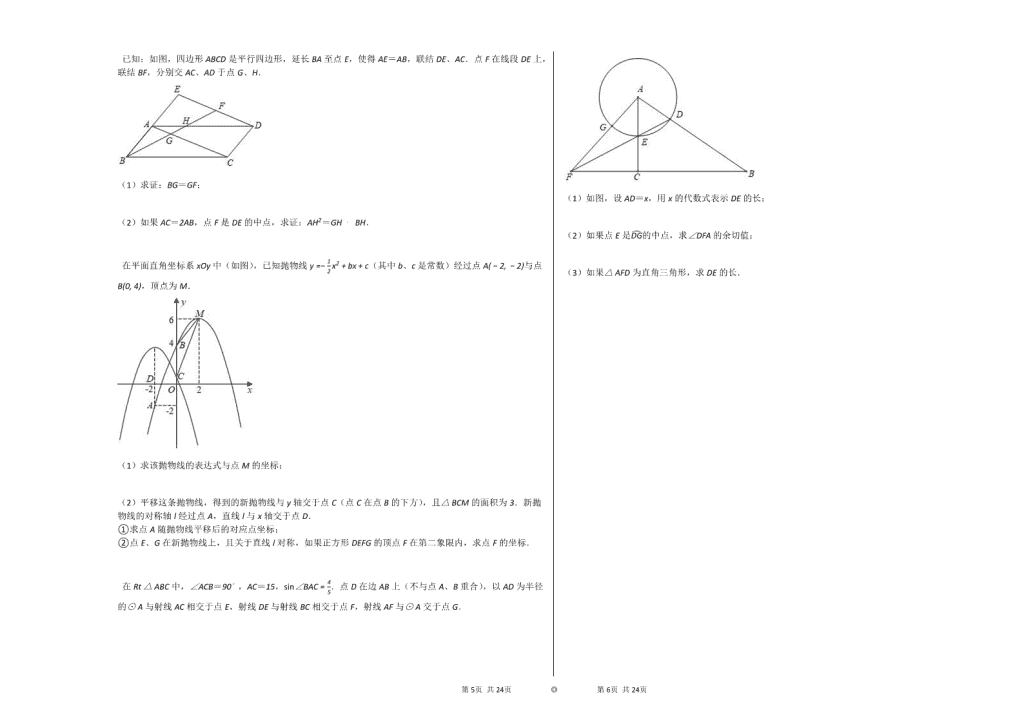
‎2020年上海市静安区中考数学二模试卷 一、选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B铅笔正确填涂]‎ ‎ ‎ ‎1. 下列二次根式中，是最简二次根式的为（ ） ‎ A.‎3a B.a‎3‎ C.‎27a D.‎a‎3‎ ‎ ‎ ‎2. 一天时间为‎86400‎秒，用科学记数法表示这一数字是（ ） ‎ A.‎864×‎‎10‎‎2‎ B.‎86.4×‎‎10‎‎3‎ C.‎8.64×‎‎10‎‎4‎ D.‎‎0.864×‎‎10‎‎5‎ ‎ ‎ ‎3. 如果关于x的方程x‎2‎‎+2x+m‎=0‎有实数根，那么m的取值范围是(        ) ‎ A.m<1‎ B.m≤1‎ C.m>1‎ D.‎m≥1‎ ‎ ‎ ‎4. 体育课上，甲同学练习双手头上前掷实心球，测得他‎5‎次投掷的成绩为：‎8‎，‎8.5‎，‎9.2‎，‎8.5‎，‎8.8‎（单位：米），那么这组数据的平均数、中位数分别是（ ） ‎ A.‎8.5‎，‎8.6‎ B.‎8.5‎，‎8.5‎ C.‎8.6‎，‎9.2‎ D.‎8.6‎，‎‎8.5‎ ‎ ‎ ‎5. 如图，‎▱ABCD的对角线AC、BD相交于点O，那么下列条件中，能判断‎▱ABCD是菱形的为（ ） ‎ A.AO＝CO B.AO＝BO C.‎∠AOB＝‎∠BOC D.‎∠BAD＝‎∠ABC ‎ ‎ ‎ ‎6. 如图，将‎△ABC绕点A逆时针旋转得到‎△ADE，其中点B、C分别与点D、E对应，如果B、D、C三点恰好在同一直线上，那么下列结论错误的是（ ） ‎ A.‎∠ACB＝‎∠AED B.‎∠BAD＝‎∠CAE C.‎∠ADE＝‎∠ACE D.‎∠DAC＝‎∠CDE ‎ 二、填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]‎ ‎ ‎ ‎ 计算：a‎11‎‎÷‎a‎7‎＝________． ‎ ‎ ‎ ‎ 因式分解：x‎2‎‎−9=‎________． ‎ ‎ ‎ ‎ 不等式组‎3x+2>x,‎x−1<0‎‎ ‎的解集是________． ‎ ‎ ‎ ‎ 方程x−4‎‎⋅x+2‎=0‎的根为________． ‎ ‎ ‎ ‎ 如果反比例函数y=kx(k是常数，k≠0)‎的图象经过点‎(−5, −1)‎，那么在这个函数图象所在的每个象限内，y的值随x的值增大而________（填“增大”或“减小”）． ‎ ‎ ‎ ‎ 在四张完全相同的卡片上，分别画有：正三角形、正八边形、圆和矩形．如果从中任意抽取‎1‎张卡片，那么这张卡片上所画图形既是轴对称图形又是中心对称图形的概率是________． ‎ ‎ ‎ ‎ 为了解某区‎24000‎名初中生平均每天的体锻时间，随机调查了该区‎300‎名初中生．如图是根据调查结果绘制成的频数分布直方图（每小组数据含最小值，不含最大值），由此可估计该区初中生平均每天的体锻时间不少于‎1.5‎小时的人数大约为________人． ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ ‎ ‎ ‎ ‎ 运输两批救援物资：第一批‎220‎吨，用‎4‎节火车皮和‎5‎辆货车正好装完；第二批‎158‎吨，用‎3‎节火车皮和‎2‎辆货车正好装完．如果每节火车皮的运载量相同，每辆货车的运载量相同，那么一节火车皮和一辆货车共装救援物资________吨． ‎ ‎ ‎ ‎ 如图，在‎△ABC中，点D在边AB上，AB＝‎4AD，设AB‎→‎‎=‎a‎→‎，AC‎→‎‎=‎b‎→‎，那么向量DC‎→‎用向量a‎→‎、b‎→‎表示为________． ‎ ‎ ‎ ‎ 如图，已知AB是‎⊙O的直径，弦CD交AB于点E，‎∠CEA＝‎30‎‎∘‎，OF⊥CD，垂足为点F，DE＝‎5‎，OF＝‎1‎，那么CD＝________． ‎ ‎ ‎ ‎ 已知矩形ABCD，对角线AC与BD相交于点O，AB＝‎6‎，BC＝‎8‎，分别以点O、D为圆心画圆，如果‎⊙O与直线AD相交、与直线CD相离，且‎⊙D与‎⊙O内切，那么‎⊙D的半径长r的取值范围是________． ‎ ‎ ‎ ‎ 如果一条直线把一个四边形分成两部分，这两部分图形的周长相等，那么这条直线称为这个四边形的“等分周长线”．在直角梯形ABCD中，AB // CD，‎∠A＝‎90‎‎∘‎，DC＝AD，‎∠B是锐角，cotB=‎‎5‎‎12‎，AB＝‎17‎．如果点E在梯形的边上，CE是梯形ABCD的“等分周长线”，那么‎△BCE的周长为________． ‎ 三、解答题：（本大题共7题，满分78分）[将下列各题的解答过程，做在答题纸的相应位置上]‎ ‎ ‎ ‎ 计算：‎(‎2‎−1‎)‎‎2‎+(‎1‎‎2‎‎)‎‎−2‎+‎1‎‎2‎‎+1‎−‎‎8‎‎1‎‎2‎． ‎ ‎ ‎ ‎ 解方程：‎1‎x+1‎‎+‎2‎x‎2‎‎−1‎=1‎． ‎ ‎ ‎ ‎ 已知：如图，在Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，BC＝‎12‎，cosB=‎‎2‎‎3‎，D、E分别是AB、BC边上的中点，AE与CD相交于点G． ‎ ‎（1）求CG的长；‎ ‎ ‎ ‎（2）求tan∠BAE的值．‎ ‎ ‎ ‎ 疫情期间，甲厂欲购买某种无纺布生产口罩，A、B两家无纺布公司各自给出了该种无纺布的销售方案． A公司方案：无纺布的价格y（万元）与其重量x（吨）是如图所示的函数关系； B公司方案：无纺布不超过‎30‎吨时，每吨收费‎2‎万元；超过‎30‎吨时，超过的部分每吨收费‎1.9‎万元． ‎ ‎（1）求如图所示的y与x的函数解析式；（不要求写出定义域）‎ ‎ ‎ ‎（2）如果甲厂所需购买的无纺布是‎40‎吨，试通过计算说明选择哪家公司费用较少．‎ ‎ ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使得AE＝AB，联结DE、AC．点F在线段DE上，联结BF，分别交AC、AD于点G、H． ‎ ‎（1）求证：BG＝GF；‎ ‎ ‎ ‎（2）如果AC＝‎2AB，点F是DE的中点，求证：AH‎2‎＝GH⋅BH．‎ ‎ ‎ ‎ 在平面直角坐标系xOy中（如图），已知抛物线y=−‎1‎‎2‎x‎2‎+bx+c（其中b、c是常数）经过点A(−2, −2)‎与点B(0, 4)‎，顶点为M． ‎ ‎（1）求该抛物线的表达式与点M的坐标；‎ ‎ ‎ ‎（2）平移这条抛物线，得到的新抛物线与y轴交于点C（点C在点B的下方），且‎△BCM的面积为‎3‎．新抛物线的对称轴l经过点A，直线l与x轴交于点D． ①求点A随抛物线平移后的对应点坐标； ②点E、G在新抛物线上，且关于直线l对称，如果正方形DEFG的顶点F在第二象限内，求点F的坐标．‎ ‎ ‎ ‎ 在Rt△ABC中，‎∠ACB＝‎90‎‎∘‎，AC＝‎15‎，sin∠BAC=‎‎4‎‎5‎．点D在边AB上（不与点A、B重合），以AD为半径的‎⊙A与射线AC相交于点E，射线DE与射线BC相交于点F，射线AF与‎⊙A交于点G． ‎ ‎（1）如图，设AD＝x，用x的代数式表示DE的长；‎ ‎ ‎ ‎（2）如果点E是DG的中点，求‎∠DFA的余切值；‎ ‎ ‎ ‎（3）如果‎△AFD为直角三角形，求DE的长．‎ 第21页 共24页 ◎ 第22页 共24页 参考答案与试题解析 ‎2020年上海市静安区中考数学二模试卷 一、选择题：（本大题共6题，每题4分，满分24分）[每小题只有一个正确选项，在答题纸相应题号的选项上用2B铅笔正确填涂]‎ ‎1.‎ ‎【答案】‎ A ‎【考点】‎ 最简二次根式 ‎【解析】‎ 根据最简二次根式的概念进行分析即可．‎ ‎【解答】‎ A‎、‎3a是最简二次根式，故此选项符合题意； B、a‎3‎‎=aa，故a‎3‎不是最简二次根式，故此选项不符合题意； C、‎27a‎=3‎‎3a，故‎27a不是最简二次根式，故此选项不符合题意； D、a‎3‎‎=‎‎3a‎3‎，故a‎3‎不是最简二次根式，故此选项不符合题意；‎ ‎2.‎ ‎【答案】‎ C ‎【考点】‎ 科学记数法--表示较大的数 ‎【解析】‎ 用科学记数法表示较大的数时，一般形式为a×‎‎10‎n，其中‎1≤|a|<10‎，n为整数，据此判断即可．‎ ‎【解答】‎ ‎86400‎‎＝‎8.64×‎‎10‎‎4‎．‎ ‎3.‎ ‎【答案】‎ B ‎【考点】‎ 根的判别式 ‎【解析】‎ 由关于x的方程x‎2‎‎+2x+m＝‎0‎有实数根知‎△‎＝b‎2‎‎−4ac≥0‎，据此求解可得．‎ ‎【解答】‎ 解：根据题意得： Δ=‎2‎‎2‎−4m≥0‎， 解得m≤1‎. 故选B.‎ ‎4.‎ ‎【答案】‎ D ‎【考点】‎ 算术平均数 中位数 ‎【解析】‎ 直接根据平均数和中位数的概念求解可得．‎ ‎【解答】‎ 这组数据的平均数为‎1‎‎5‎‎×(8+8.5+9.2+8.5+8.8)‎＝‎8.6‎， 将数据重新排列为‎8‎、‎8.5‎、‎8.5‎、‎8.8‎、‎9.2‎， 所以这组数据的中位数为‎8.5‎，‎ ‎5.‎ ‎【答案】‎ C ‎【考点】‎ 平行四边形的性质 菱形的性质 菱形的判定 ‎【解析】‎ 在平行四边形基础上，菱形的判定方法有：①一组邻边相等的平行四边形是菱形；②对角线互相垂直的平行四边形是菱形．据此逐个选项分析即可．‎ ‎【解答】‎ 选项A，由平行四边形的性质可知，对角线互相平分，故A不符合题意； 选项B，由‎▱ABCD中AO＝BO可推得AC＝BD，可以证明‎▱ABCD为矩形，但不能判定‎▱ABCD为菱形，故B不符合题意； 选项C，当‎∠AOB＝‎∠BOC时，由于‎∠AOB+∠BOC＝‎180‎‎∘‎，故‎∠AOB＝‎∠BOC＝‎90‎‎∘‎，而对角线互相垂直的平行四边形是菱形，故C符合题意； 选项D，由平行四边形的性质可知，‎∠BAD+∠ABC＝‎180‎‎∘‎，故当‎∠BAD＝‎∠ABC时，‎∠BAD＝‎∠ABC＝‎90‎‎∘‎，从而可判定‎▱ABCD为矩形，故D不符合题意． 综上，只有选项C可以判定‎▱ABCD是菱形．‎ ‎6.‎ ‎【答案】‎ D ‎【考点】‎ 旋转的性质 ‎【解析】‎ 利用旋转的性质直接对A选项进行判断；利用旋转的性质得‎∠BAC＝‎∠DAE，再利用三角形外角性质得‎∠BAD＝‎∠CAE，则可对B选项进行判断；利用旋转的性质得‎∠ADE＝‎∠B，AB＝AD，AC＝AE，然后根据等腰三角形顶角相等时底角相等得到‎∠B＝‎∠ACE，则‎∠ADE＝‎∠ACE，于是可对C选项进行判断；先判断‎∠EDC＝‎∠BAD，而‎∠BAD不能确定等于‎∠DAC，则可对D选项进行判断．‎ ‎【解答】‎ ‎∵ ‎△ABC绕点A逆时针旋转得到‎△ADE， ∴ ‎∠ACB＝‎∠AED，所以A选项的结论正确； ‎∠BAC＝‎∠DAE， 即‎∠BAD+∠DAC＝‎∠DAC+∠CAE， ∴ ‎∠BAD＝‎∠CAE，所以B选项的结论正确； ∵ ‎△ABC绕点A 第21页 共24页 ◎ 第22页 共24页 逆时针旋转得到‎△ADE， ∴ ‎∠ADE＝‎∠B，AB＝AD，AC＝AE， ∵ ‎∠BAD＝‎∠CAE， ∴ ‎∠B＝‎∠ACE， ∴ ‎∠ADE＝‎∠ACE，所以C选项的结论正确； ∵ ‎∠ADC＝‎∠B+∠BAD， 而‎∠ADE＝‎∠B， ∴ ‎∠EDC＝‎∠BAD， 而AD不能确定平分‎∠BAC， ∴ ‎∠BAD不能确定等于‎∠DAC， ∴ ‎∠EDC不能确定等于‎∠DAC，所以D选项的结论错误．‎ 二、填空题：（本大题共12题，每题4分，满分48分）[在答题纸相应题号后的空格内直接填写答案]‎ ‎【答案】‎ a‎4‎ ‎【考点】‎ 同底数幂的除法 ‎【解析】‎ 直接利用同底数幂的除法运算法则计算得出答案．‎ ‎【解答】‎ a‎11‎‎÷‎a‎7‎‎＝a‎4‎．‎ ‎【答案】‎ ‎(x+3)(x−3)‎ ‎【考点】‎ 因式分解-运用公式法 ‎【解析】‎ 原式利用平方差公式分解即可．‎ ‎【解答】‎ 解：原式‎=(x+3)(x−3)‎. 故答案为：‎(x+3)(x−3)‎.‎ ‎【答案】‎ ‎−1x，得：x>−1‎， 解不等式x−1<0‎，得：x<1‎， 则不等式组的解集为‎−10‎， 所以这个函数图象所在的每个象限内，y的值随自变量x值的增大而减小．‎ ‎【答案】‎ ‎3‎‎4‎ ‎【考点】‎ 概率公式 轴对称图形 中心对称图形 ‎【解析】‎ 直接利用轴对称图形和中心对称图形的定义得出符合题意的图形个数，进而得出概率．‎ ‎【解答】‎ 正三角形、正八边形、圆和矩形中既是轴对称图形又是中心对称图形是正八边形、圆和矩形． 故这张卡片上所画图形既是轴对称图形又是中心对称图形的概率是：‎3‎‎4‎．‎ ‎【答案】‎ ‎4800‎ ‎【考点】‎ 用样本估计总体 频数（率）分布直方图 ‎【解析】‎ 用总人数乘以样本中每天的体锻时间不少于‎1.5‎小时的人数占被调查人数的比例即可得．‎ ‎【解答】‎ 估计该区初中生平均每天的体锻时间不少于‎1.5‎小时的人数大约为‎24000×‎300−20−100−120‎‎300‎=4800‎（人），‎ ‎【答案】‎ ‎54‎ ‎【考点】‎ 二元一次方程组的应用——行程问题 第21页 共24页 ◎ 第22页 共24页 二元一次方程的应用 二元一次方程组的应用——其他问题 一元一次方程的应用——工程进度问题 一元一次方程的应用——其他问题 ‎【解析】‎ 设一节火车皮装救援物资x吨，一辆货车装救援物资y吨，由题意得等量关系：‎4‎节火车皮运载量‎+5‎辆货车运载量＝‎220‎吨，‎3‎节火车皮运载量‎+2‎辆货车运载量＝‎158‎吨，根据等量关系列出方程组，再解即可．‎ ‎【解答】‎ 设一节火车皮装救援物资x吨，一辆货车装救援物资y吨，由题意得： ‎4x+5y=220‎‎3x+2y=158‎‎ ‎， 解得：x=50‎y=4‎‎ ‎， 则一节火车皮和一辆货车共装救援物资：‎50+4‎＝‎54‎（吨），‎ ‎【答案】‎ ‎−‎1‎‎4‎a‎→‎+‎b‎→‎ ‎【考点】‎ ‎*平面向量 ‎【解析】‎ 利用三角形法则：DC‎→‎‎=DA‎→‎+‎AC‎→‎求解即可．‎ ‎【解答】‎ ‎∵ AB＝‎4AD， ∴ AD=‎1‎‎4‎AB， ∴ AD‎→‎‎=‎‎1‎‎4‎AB‎→‎， ∵ DC‎→‎‎=DA‎→‎+‎AC‎→‎， ∴ DC‎→‎‎=−‎1‎‎4‎a‎→‎+‎b‎→‎，‎ ‎【答案】‎ ‎10−2‎‎3‎ ‎【考点】‎ 垂径定理 勾股定理 ‎【解析】‎ 根据AB是‎⊙O的直径，OF⊥CD，和垂径定理可得CF＝DF，再根据‎30‎度角所对直角边等于斜边一半，和勾股定理即可求出EF的长，进而可得CD的长．‎ ‎【解答】‎ ‎∵ AB是‎⊙O的直径，OF⊥CD， 根据垂径定理可知： CF＝DF， ∵ ‎∠CEA＝‎30‎‎∘‎， ∴ ‎∠OEF＝‎30‎‎∘‎， ∴ OE＝‎2‎，EF=‎‎3‎， ∴ DF＝DE−EF＝‎5−‎‎3‎， ∴ CD＝‎2DF＝‎10−2‎‎3‎．‎ ‎【答案】‎ ‎8‎r‎1‎，否则‎⊙D与‎⊙O不能内切， ∵ OD=‎1‎‎2‎AC＝‎5‎， ∴ 圆心距d＝‎5‎， ∴ d＝r−‎r‎1‎， ∴ r＝‎5+‎r‎1‎， ∴ ‎80‎． ∴ EG＝DF＝‎2EH＝‎2DH＝‎2a． 不妨设点E在点G的右侧，那么E(−2+a, a)‎． 将点E代入y=−‎1‎‎2‎(x+2‎)‎‎2‎+3‎，得‎−‎1‎‎2‎a‎2‎+3=a， 解得，a‎1‎‎=‎7‎−1‎，a‎2‎‎=−‎7‎−1‎（不合题意，舍去）． ∴ F(−2, 2‎7‎−2)‎．‎ ‎【考点】‎ 待定系数法求二次函数解析式 二次函数图象上点的坐标特征 二次函数图象与几何变换 正方形的性质 二次函数的性质 ‎【解析】‎ ‎（1）根据抛物线y=−‎1‎‎2‎x‎2‎+bx+c（其中b、c是常数）经过点A(−2, −2)‎与点B(0, 4)‎，从而可以求得抛物线的解析式，然后将解析式化为顶点式，即可得到顶点M的坐标； （2）①根据题意，可以求得平移后新抛物线的解析式，从而可以得到点A随抛物线平移后的对应点坐标； ②根据题意和正方形的性质，可以求得点F的坐标．‎ ‎【解答】‎ 第21页 共24页 ◎ 第22页 共24页 将A(−2, −2)‎、B(0, 4)‎代入y=−‎1‎‎2‎x‎2‎+bx+c中， ‎−‎1‎‎2‎×‎(−2)‎‎2‎−2b+c=−2,‎‎0+0+c=4.‎‎ ‎ 解得b=2,‎c=4.‎‎ ‎ ∴ 该抛物线的表达式为：y=−‎1‎‎2‎x‎2‎+2x+4‎； ∵ y=−‎1‎‎2‎x‎2‎+2x+4=−‎1‎‎2‎(x−2‎)‎‎2‎+6‎， ∴ 顶点M的坐标是：‎(2, 6)‎；‎ ‎①∵ 平移后抛物线的对称轴经过点A(−2, −2)‎， ∴ 可设平移后的抛物线表达式为：y=−‎1‎‎2‎(x+2‎)‎‎2‎+k， ∴ C(0, −2+k)‎． ∴ S‎△BCM‎=‎1‎‎2‎BC⋅2=‎1‎‎2‎[4−(−2+k)]⋅2=3‎， 解得，k＝‎3‎． ∴ y=−‎1‎‎2‎(x+2‎)‎‎2‎+3‎， 即原抛物线向左平移‎4‎个单位，向下平移‎3‎个单位可以得到新的抛物线． ∴ 点A对应点的坐标为‎(−6, −5)‎； ②设EG与DF的交点为H，在正方形DEFG中，EG⊥DF，EG＝DF＝‎2EH＝‎2DH． ∵ 点E、G是这条抛物线上的一对对称点， ∴ EG // x轴． ∴ DF⊥x轴， 设F(−2, 2a)‎． ∵ 点F在第二象限内， ∴ a>0‎． ∴ EG＝DF＝‎2EH＝‎2DH＝‎2a． 不妨设点E在点G的右侧，那么E(−2+a, a)‎． 将点E代入y=−‎1‎‎2‎(x+2‎)‎‎2‎+3‎，得‎−‎1‎‎2‎a‎2‎+3=a， 解得，a‎1‎‎=‎7‎−1‎，a‎2‎‎=−‎7‎−1‎（不合题意，舍去）． ∴ F(−2, 2‎7‎−2)‎．‎ ‎【答案】‎ 如图， 过点D作DH⊥AC，垂足为H． 在Rt△AEH中，DH=AD⋅sin∠BAC=‎4‎‎5‎x， AH=AD‎2‎−DH‎2‎=‎3‎‎5‎x． 在‎⊙A中，AE＝AD＝x， ∴ EH=AE−AD=x−‎3‎‎5‎x=‎2‎‎5‎x， ∴ DE=EH‎2‎+DH‎2‎=‎2‎‎5‎‎5‎x；‎ ‎∵ sin∠BAC=BCAB=‎‎4‎‎5‎， ∴ 可设BC＝‎4k(k>0)‎，AB＝‎5k， 则AC=AB‎2‎−BC‎2‎=3k． ∵ AC＝‎15‎， ∴ ‎3k＝‎15‎， ∴ k＝‎5‎． ∴ BC＝‎20‎，AB＝‎25‎． ∵ 点E是DG的中点，由题意可知此时点E在边AC上，点F在BC的延长线上， ∴ ‎∠FAC＝‎∠BAC． ∵ ‎∠FCA＝‎∠BCA＝‎90‎‎∘‎，AC＝AC， ∴ ‎△FCA≅△BCA(ASA)‎， ∴ FC＝BC＝‎20‎． ∵ tan∠AED=DHEH=‎4‎‎5‎x‎2‎‎5‎x=2‎， 又∵ ‎∠AED＝‎∠FEC，且‎∠AED、‎∠FEC都为锐角， ∴ tan∠FEC＝‎2‎． ∴ EC=FCtan∠FEC=‎20‎‎2‎=10‎． ∴ AE＝AC−EC＝‎20−10‎＝‎5‎． 过点A作AM⊥DE，垂足为M， 则EM=‎1‎‎2‎ED=‎1‎‎2‎×‎2‎‎5‎‎5‎×5=‎‎5‎． ∵ sin∠AED=DHED=‎4‎‎5‎x‎2‎‎5‎‎5‎x=‎‎2‎‎5‎‎5‎， ∴ AM=AE⋅sin∠AED=‎2‎‎5‎‎5‎×5=2‎‎5‎． 在Rt△EFC中，EF=EC‎2‎+FC‎2‎=10‎‎5‎． ∴ 在Rt△AFM中，cot∠AFD=FMAM=FE+EMAM=‎10‎5‎+‎‎5‎‎2‎‎5‎=‎‎11‎‎2‎． 答：‎∠DFA的余切值为‎11‎‎2‎；‎ 当点E在AC上时，只有可能‎∠FAD＝‎90‎‎∘‎． ∵ FC＝CE⋅tan∠FEC＝‎2(15−x)‎， ∴ EF=EC‎2‎+FC‎2‎=‎5‎(15−x)‎． ∴ FD=EF+ED=‎5‎(15−x)+‎2‎‎5‎‎5‎x=15‎5‎−‎3‎‎5‎‎5‎x． ∵ cos∠AED=EHDH=‎‎5‎‎5‎， 又∵ ‎∠AED＝‎∠ADE，且‎∠AED、‎∠ADE都为锐角， ∴ cos∠ADE=cos∠AED=‎‎5‎‎5‎． ∴ cos∠ADE=ADDF=x‎15‎5‎−‎3‎‎5‎‎5‎x=‎‎5‎‎5‎． ∴ AD＝x=‎‎75‎‎8‎． ∴ DE=‎2‎‎5‎‎5‎x=‎2‎‎5‎‎5‎×‎75‎‎8‎=‎‎15‎‎5‎‎4‎． 当点E在AC的延长线上时，只有可能‎∠AFD＝‎90‎‎∘‎，此时‎∠AFC＝‎∠AEF． ∵ ‎∠AFC、‎∠AEF都为锐角， ∴ tan∠AEF＝tan∠AFC＝‎2‎． ∵ CE＝AE−AC＝x−15‎， ∴ CF＝CE⋅tan∠AEF＝‎2(x−15)‎． ∴ ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ tan∠AFC=ACCF=‎15‎‎2(x−15)‎=2‎． ∴ AD＝x=‎‎75‎‎4‎． ∴ DE=‎2‎‎5‎‎5‎x=‎2‎‎5‎‎5‎×‎75‎‎4‎=‎‎15‎‎5‎‎2‎． 综上所述，‎△AFD为直角三角形时，DE的长为‎15‎‎5‎‎4‎或‎15‎‎5‎‎2‎．‎ ‎【考点】‎ 圆的综合题 ‎【解析】‎ ‎（1）过点D作DH⊥AC，垂足为H．根据锐角三角函数和勾股定理即可用x的代数式表示DE的长； （2）根据题意可设BC＝‎4k(k>0)‎，AB＝‎5k，则AC=AB‎2‎−BC‎2‎=3k．过点A作AM⊥DE，垂足为M，再根据锐角三角函数和勾股定理即可表示‎∠DFA的余切值； （3）分两种情况讨论：当点E在AC上时，只有可能‎∠FAD＝‎90‎‎∘‎；当点E在AC的延长线上时，只有可能‎∠AFD＝‎90‎‎∘‎，此时‎∠AFC＝‎∠AEF．根据锐角三角函数和勾股定理即可求DE的长．‎ ‎【解答】‎ 如图， 过点D作DH⊥AC，垂足为H． 在Rt△AEH中，DH=AD⋅sin∠BAC=‎4‎‎5‎x， AH=AD‎2‎−DH‎2‎=‎3‎‎5‎x． 在‎⊙A中，AE＝AD＝x， ∴ EH=AE−AD=x−‎3‎‎5‎x=‎2‎‎5‎x， ∴ DE=EH‎2‎+DH‎2‎=‎2‎‎5‎‎5‎x；‎ ‎∵ sin∠BAC=BCAB=‎‎4‎‎5‎， ∴ 可设BC＝‎4k(k>0)‎，AB＝‎5k， 则AC=AB‎2‎−BC‎2‎=3k． ∵ AC＝‎15‎， ∴ ‎3k＝‎15‎， ∴ k＝‎5‎． ∴ BC＝‎20‎，AB＝‎25‎． ∵ 点E是DG的中点，由题意可知此时点E在边AC上，点F在BC的延长线上， ∴ ‎∠FAC＝‎∠BAC． ∵ ‎∠FCA＝‎∠BCA＝‎90‎‎∘‎，AC＝AC， ∴ ‎△FCA≅△BCA(ASA)‎， ∴ FC＝BC＝‎20‎． ∵ tan∠AED=DHEH=‎4‎‎5‎x‎2‎‎5‎x=2‎， 又∵ ‎∠AED＝‎∠FEC，且‎∠AED、‎∠FEC都为锐角， ∴ tan∠FEC＝‎2‎． ∴ EC=FCtan∠FEC=‎20‎‎2‎=10‎． ∴ AE＝AC−EC＝‎20−10‎＝‎5‎． 过点A作AM⊥DE，垂足为M， 则EM=‎1‎‎2‎ED=‎1‎‎2‎×‎2‎‎5‎‎5‎×5=‎‎5‎． ∵ sin∠AED=DHED=‎4‎‎5‎x‎2‎‎5‎‎5‎x=‎‎2‎‎5‎‎5‎， ∴ AM=AE⋅sin∠AED=‎2‎‎5‎‎5‎×5=2‎‎5‎． 在Rt△EFC中，EF=EC‎2‎+FC‎2‎=10‎‎5‎． ∴ 在Rt△AFM中，cot∠AFD=FMAM=FE+EMAM=‎10‎5‎+‎‎5‎‎2‎‎5‎=‎‎11‎‎2‎． 答：‎∠DFA的余切值为‎11‎‎2‎；‎ 当点E在AC上时，只有可能‎∠FAD＝‎90‎‎∘‎． ∵ FC＝CE⋅tan∠FEC＝‎2(15−x)‎， ∴ EF=EC‎2‎+FC‎2‎=‎5‎(15−x)‎． ∴ FD=EF+ED=‎5‎(15−x)+‎2‎‎5‎‎5‎x=15‎5‎−‎3‎‎5‎‎5‎x． ∵ cos∠AED=EHDH=‎‎5‎‎5‎， 又∵ ‎∠AED＝‎∠ADE，且‎∠AED、‎∠ADE都为锐角， ∴ cos∠ADE=cos∠AED=‎‎5‎‎5‎． ∴ cos∠ADE=ADDF=x‎15‎5‎−‎3‎‎5‎‎5‎x=‎‎5‎‎5‎． ∴ AD＝x=‎‎75‎‎8‎． ∴ DE=‎2‎‎5‎‎5‎x=‎2‎‎5‎‎5‎×‎75‎‎8‎=‎‎15‎‎5‎‎4‎． 当点E在AC的延长线上时，只有可能‎∠AFD＝‎90‎‎∘‎，此时‎∠AFC＝‎∠AEF． ∵ ‎∠AFC、‎∠AEF都为锐角， ∴ tan∠AEF＝tan∠AFC＝‎2‎． ∵ CE＝AE−AC＝x−15‎， ∴ CF＝CE⋅tan∠AEF＝‎2(x−15)‎． ∴ ‎ 第21页 共24页 ◎ 第22页 共24页 ‎ tan∠AFC=ACCF=‎15‎‎2(x−15)‎=2‎． ∴ AD＝x=‎‎75‎‎4‎． ∴ DE=‎2‎‎5‎‎5‎x=‎2‎‎5‎‎5‎×‎75‎‎4‎=‎‎15‎‎5‎‎2‎． 综上所述，‎△AFD为直角三角形时，DE的长为‎15‎‎5‎‎4‎或‎15‎‎5‎‎2‎．‎ 第21页 共24页 ◎ 第22页 共24页