2010中考数学桂林考试试题

2010中考数学桂林考试试题

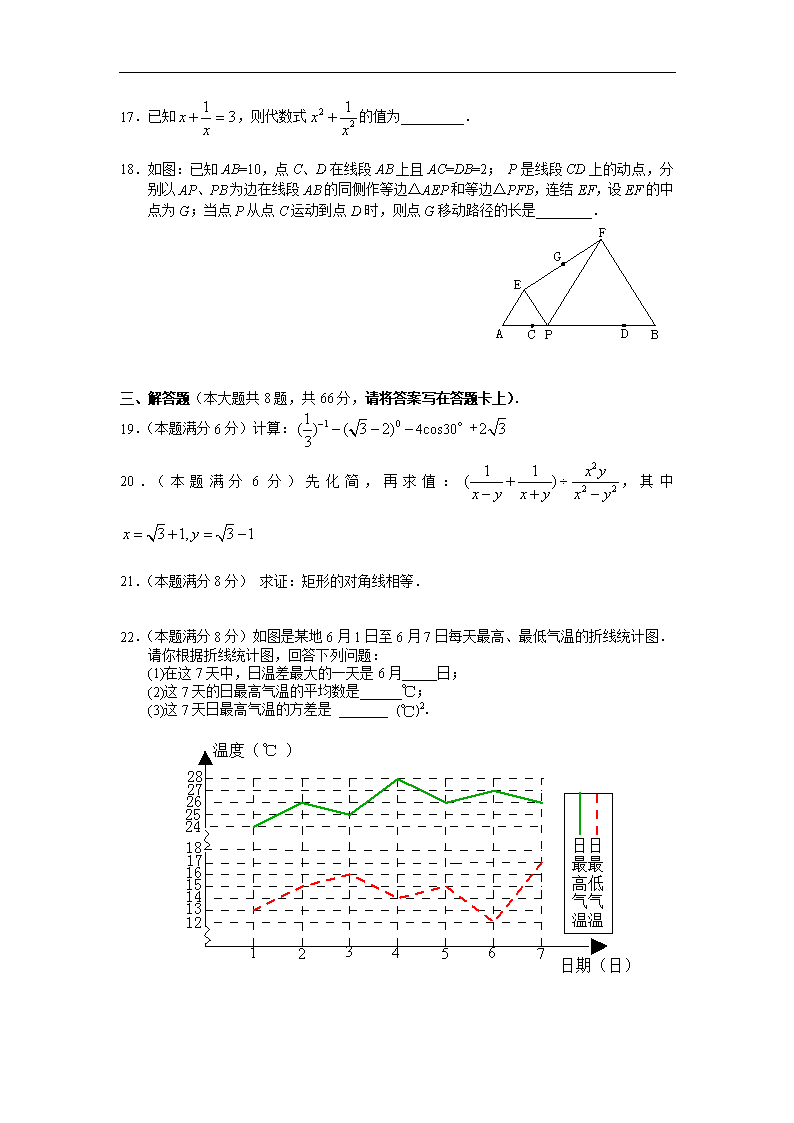
‎2010年桂林市初中毕业升学考试试卷 数 学 ‎（考试用时：120分钟 满分： 120分）‎ 注意事项：‎ ‎1．本试卷分选择题和非选择题两部分．在本试卷上作答无效．‎ ‎2．考试结束后，将本试卷和答题卡一并交回．‎ ‎3．答题前，请认真阅读答题卡上的注意事项．‎ 一、选择题（共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑）．‎ ‎1．的绝对值是（ ）． ‎ A． B．‎2 C． D．‎ ‎2．在实数5、、、中，无理数是（ ）．‎ A．5 B． C． D．‎ ‎3．如图，直线AB、CD被直线EF所截，‎ 则∠3的同旁内角是（ ）．‎ A．∠1 B．∠2 ‎ ‎ C．∠4 D．∠5‎ ‎4． 如图所示几何体的左视图是（ ）．‎ A．‎ B．‎ C．‎ D．‎ ‎5．下列运算正确的是（ ）．‎ A．＝ B． C． D．‎ ‎6．如图，已知△ADE与△ABC的相似比为1：2，则△ADE 与△ABC的面积比为（ ）．‎ A． 1：2 B． 1：4 ‎ C． 2：1 D． 4：1‎ ‎7．若反比例函数的图象经过点（－3，2），则的值为 （ ）．‎ A．－6 B．‎6 C．-5 D．5‎ ‎ ‎ ‎8．一元二次方程的解是 （ ）．‎ A．， B．，‎ C．， D．，‎ ‎9．下列说法正确的是（ ）．‎ A．买一张福利彩票一定中奖，是必然事件． ‎ B．买一张福利彩票一定中奖，是不可能事件．‎ C．抛掷一个正方体骰子，点数为奇数的概率是．‎ D．一组数据：1，7，3，5，3的众数是3．‎ ‎10．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是 （ ）．‎ A． B． ‎ C． D． ‎ ‎11．将抛物线绕它的顶点旋转180°，所得抛物线的解析式是（ ）．‎ ‎ A． B．‎ C． D．‎ ‎12．如图，已知正方形ABCD的边长为4 ，E是BC边上的一个 动点，AE⊥EF， EF交DC于F, 设BE=，FC=，则当 点E从点B运动到点C时,关于的函数图象是( )．‎ A． B． C． D．‎ 二、填空题（共6小题，每小题3分，共18分，请将答案填在答题卡上）．‎ ‎13．因式分解：= ． ‎ ‎14．情系玉树大爱无疆，截至‎5月21日12时，青海玉树共接收国内外地震救灾捐赠 款物551300万元，将551300万元用科学记数法表示为__________万元．‎ ‎15．函数的自变量的取值范围是 ．‎ ‎16．正五边形的内角和等于______度．‎ ‎17．已知，则代数式的值为_________．‎ ‎18．如图：已知AB=10，点C、D在线段AB上且AC=DB=2； P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是________．‎ 三、解答题（本大题共8题，共66分，请将答案写在答题卡上）．‎ ‎19．（本题满分6分）计算：4cos30°+‎ ‎20．（本题满分6分）先化简，再求值：，其中 ‎ ‎ ‎21．（本题满分8分） 求证：矩形的对角线相等．‎ ‎22．（本题满分8分）如图是某地‎6月1日至‎6月7日每天最高、最低气温的折线统计图．‎ 请你根据折线统计图，回答下列问题：‎ ‎(1)在这7天中，日温差最大的一天是6月_____日；‎ ‎(℃) ‎ ‎2‎ ‎(2)这7天的日最高气温的平均数是______℃；‎ ‎(3)这7天日最高气温的方差是 _______ ． ‎ ‎℃‎ ‎23．（本题满分8分）某蔬菜公司收购到某种蔬菜104吨，准备加工后上市销售. 该公司加工该种蔬菜的能力是：每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务，则该公司应安排几天精加工，几天粗加工？‎ ‎24．（本题满分8分）某校初三年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元.‎ ‎（1）该校初三年级共有多少人参加春游？‎ ‎（2）请你帮该校设计一种最省钱的租车方案． ‎ ‎25．（本题满分10分）如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，‎ FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．‎ H ‎（1）证明：AF平分∠BAC；‎ ‎（2）证明：BF＝FD；‎ ‎（3）若EF＝4，DE＝3，求AD的长．‎ ‎26．（本题满分12分）如图，过A（8，0）、B（0，）两点的直线与直线交于点C．平行于轴的直线从原点O出发，以每秒1个单位长度的速度沿轴向右平移，到C点时停止；分别交线段BC、OC于点D、E，以DE为边向左侧作等边△DEF，设△DEF与△BCO重叠部分的面积为S（平方单位），直线的运动时间为t（秒）．‎ ‎（1）直接写出C点坐标和t的取值范围； ‎ ‎（2）求S与t的函数关系式；‎ ‎（3）设直线与轴交于点P，是否存在这样的点P，使得以P、O、F为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ ‎2010年桂林市初中毕业升学考试 数学参考答案及评分标准 一、 选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C B A C B A A D C D A 二、 填空题：‎ ‎13． 14．5.513×105 15．>1 16．540 ‎ ‎17．7 18．3‎ 三、解答题：‎ ‎19．(本题 6分)解：原式= ……………………3分 ‎ = ………………………………………………5分 ‎=2 ………………………………………… 6分 ‎ ……………… 1分 ‎ = ………………………3分 ‎== …………………………………4分 ‎= ……………………………………6分 ‎21.(本题8 分)已知：四边形ABCD是矩形, AC与BD是对角线 ……………2分 求证：AC=BD ………………………………………3分 证明： ∵四边形ABCD是矩形 ‎ ‎∴AB=DC,∠ABC=∠DCB=90°…………4分 又∵BC=CB …………………………5分 ‎∴△ABC≌△DCB …………6分 ‎∴AC=BD ……………………7分 所以矩形的对角线相等. …………8分 ‎22. (本题 8分) (1)6, (2)26, (3) ［说明：(1)2分，(2)3分，(3)3分］‎ ‎23. (本题8 分)设该公司安排天粗加工, 安排天精加工.……………1分 据题意得:……………………………………4分 解得:………………………………………………7分 答: 该公司安排10天粗加工, 安排6天精加工.…………8分 ‎24. (本题8 分)解(1)设租36座的车辆.……………………………………1分 据题意得:………………………………3分 解得: ……………………………………………4分 ‎ 由题意应取8…………………………5分 则春游人数为:368=288(人).…………………………………6分 ‎(2) 方案①：租36座车8辆的费用:8400=3200元,‎ 方案②：租42座车7辆的费用:元 方案③：因为，‎ 租42座车6辆和36座车1辆的总费用:元 所以方案③：租42座车6辆和36座车1辆最省钱.…………8分 ‎（说明：只要给出方案③就可得满分2分）‎ ‎25．(本题10 分)证明（1）连结OF H ‎∵FH是⊙O的切线 ‎∴OF⊥FH ……………1分 ‎∵FH∥BC ，‎ ‎∴OF垂直平分BC ………2分 ‎∴‎ ‎∴AF平分∠BAC …………3分 ‎（2）证明：由（1）及题设条件可知 ‎∠1=∠2，∠4=∠3，∠5=∠2 ……………4分 H ‎∴∠1+∠4=∠2+∠3‎ ‎∴∠1+∠4=∠5+∠3 ……………5分 ‎∠FDB=∠FBD ‎∴BF=FD ………………6分 ‎ （3）解： 在△BFE和△AFB中 ‎∵∠5=∠2=∠1，∠F=∠F ‎∴△BFE∽△AFB ………………7分 ‎∴， ……………8分 ‎∴‎ ‎∴ ……………………9分 ‎ ‎ ∴‎ ‎∴AD== …………………10分 ‎26．(本题12 分)解（1）C（4，） ……………………………2分 的取值范围是：0≤≤4 ……………………………… 3分 ‎（2）∵D点的坐标是（，），E的坐标是（，）‎ ‎∴DE=-= ……………………4分 ‎∴等边△DEF的DE边上的高为： ‎ ‎∴当点F在BO边上时：=，∴=3 ……………………5分 ① 当0≤<3时，重叠部分为等腰梯形，可求梯形上底为：- …7分 S=‎ ‎=‎ ‎= ………………………………8分 ② 当3≤≤4时，重叠部分为等边三角形 S= ………………… 9分 ‎= ……………………10分 ‎（3）存在，P（，0） ……………………12分 说明：∵FO≥，FP≥，OP≤4‎ ‎∴以P，O，F以顶点的等腰三角形，腰只有可能是FO，FP,‎ 若FO=FP时，=2（12-3），=，∴P（，0） ‎