中考数学专题复习练习：中考中常见的直角三角形问题

中考数学专题复习练习：中考中常见的直角三角形问题

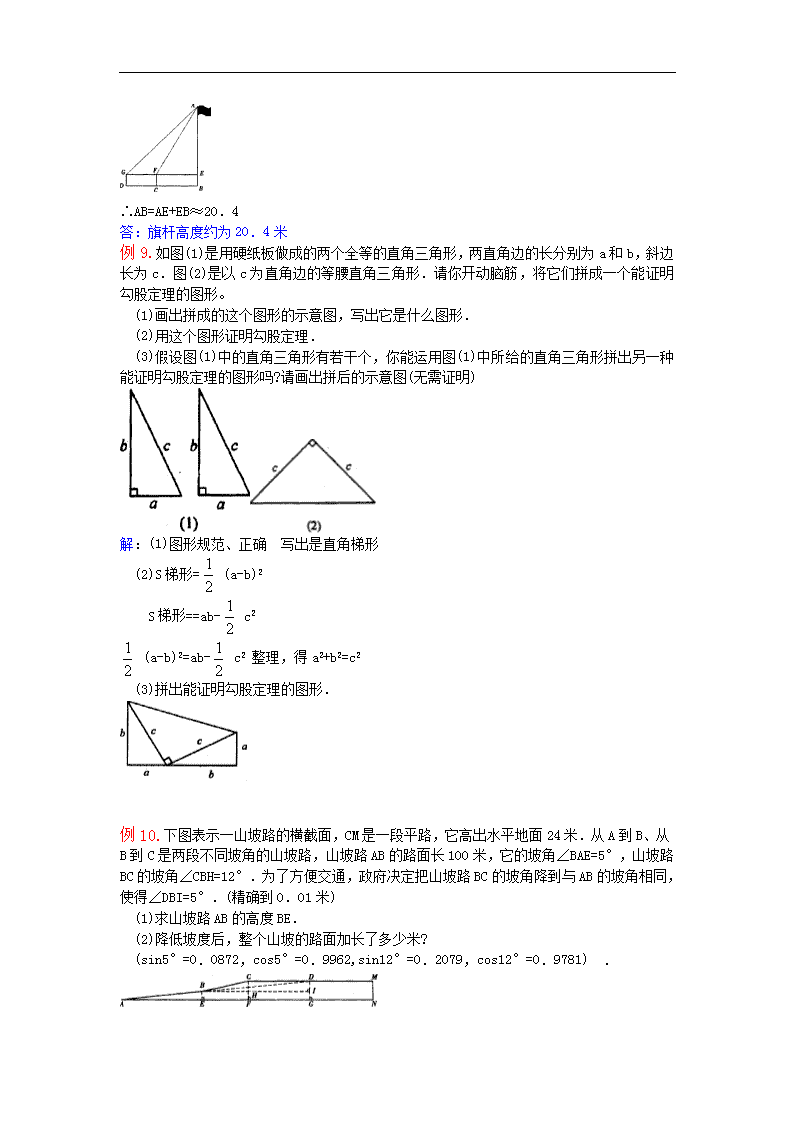
第十二章解直角三角形与中考 ‎ 中考要求及命题趋势 ‎ ‎1、理解锐角三角形函数角的三角函数的值；‎ ‎2、会由已知锐角求它的三角函数，由已知三角函数值求它对应、的锐角 ；‎ ‎3、会运用三角函数解决与直角三角形有关的简单实际问题。‎ ‎2007年将继续考查锐角三角形函数的概念，其中特殊三角函数值为考查的重点。解直角三角形为命题的热点，特别是与实际问题结合的应用题 应试对策 ‎ ‎1要掌握锐角三角函数的概念，会根据已知条件求一个角的三角函数，会熟练地运用特殊角的三角函数值，会使用科学计算器进行三角函数的求值；‎ ‎2掌握根据已知条件解直角三角形的方法，运用解直角三角形的知识解决实际问题。具体做到：1）了解某些实际问题中的仰角、俯角、坡度等概念；2）将实际问题转化为数学问题，建立数学模型；3）涉及解斜三角形的问题时，会通过作适当的辅助线构造直角三角形，使之转化为解直角三角形的计算问题而达到解决实际问题 例题精讲 ‎ 例1、在Rt△ABC中，∠C=90°，a = 1 , c = 4 , 则sinA的值是 ( )‎ A、 B、 C、 D、‎ 答案：B 例2．在A ABC中，已知∠C=90°，sinB=，则cosA的值是 ( )‎ ‎ A． B． c． D．‎ 答案：D 例3.在RtΔABC中,∠C=900,则下列等式中不正确的是( )‎ ‎（A）a=csinA；（B）a=bcotB；（C）b=csinB；‎ ‎（D）c=.‎ 答案：D 例4.为测楼房BC的高，在距楼房‎30米的A处，测得楼顶B的仰角为α,则楼房BC的高为( )B ‎（A）米；（B）米； （C）米； （D）米 答案：B 例5．在中，，，则为（ ）C ‎ A． B． C． D．‎ 答案：C 例6.如图，是一束平行的阳光从教室窗户射入的平面示意图，光线与地面所成角∠AMC=30°，在教室地面的影长MN=‎2米．若窗户的下檐到教室地面的距离BC=‎1米，则窗户的上檐到教室的距离AC为( )‎ ‎ A．‎2‎ 米 B．‎3米 c．3．‎2米 D．米 答案：B 例7.某人沿倾斜角为β的斜坡走了‎100米，则他上升的高度是 米 答案：100sinβ 例8.如图7，初三年级某班同学要测量校园内国旗旗杆的高度，在地面的C点用测角器测得旗杆顶A点的仰角∠AFE=60°，再沿直线CB后退‎8米到D点，在D点又用测角器测得旗杆顶A点的仰角∠AGE=45°；已知测角器的高度是1．‎6米，求旗杆AB的高度．(的近似值取1．7，结果保留小数)‎ 解：设AE为x米，在Rt△EF中，∠AFE=60°，‎ ‎ ∴EF=x/3‎ ‎ 在Rt△AGE中，∠AGE=45° AE=GE ‎ 8+x/3=x ∴x=12+4‎ ‎ 即x≈18．8(的近似值取1．7，结果保留小数)‎ ‎∴AB=AE+EB≈20．4‎ 答：旗杆高度约为20．‎‎4米 例9.如图(1)是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c．图(2)是以c为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个能证明勾股定理的图形。‎ ‎ (1)画出拼成的这个图形的示意图，写出它是什么图形．‎ ‎ (2)用这个图形证明勾股定理． ‎ ‎ (3)假设图(1)中的直角三角形有若干个，你能运用图(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明)‎ 解：(1)图形规范、正确 写出是直角梯形 ‎ (2)S梯形= (a-b)2 ‎ ‎ S梯形==ab- c2‎ ‎ (a-b)2=ab- c2 整理，得a2+b2=c2‎ ‎ (3)拼出能证明勾股定理的图形．‎ 例10.下图表示一山坡路的横截面，CM是一段平路，它高出水平地面‎24米．从A到B、从B到C是两段不同坡角的山坡路，山坡路AB的路面长‎100米，它的坡角∠BAE=5°，山坡路BC的坡角∠CBH=12°．为了方便交通，政府决定把山坡路BC的坡角降到与AB的坡角相同，使得∠DBI=5°．(精确到0．O‎1米)‎ ‎ (1)求山坡路AB的高度BE．‎ ‎ (2)降低坡度后，整个山坡的路面加长了多少米?‎ ‎ (sin5°=0．0872，cos5°=0．9962,sin12°=0．2079，cos12°=0．9781) ．‎ 解：(1)在Rt△ABE中，BE=8．72(米)‎ ‎ (2)在Rt△CBH中，CH=CF-HF=15．28．BC=73．497‎ ‎ 在Rt△DBI中，DB=175．229‎ ‎ ∴DB-BC≈175．229-73．497=101．732≈101．73(米)‎