2020九年级数学上册 第1章 二次函数 1

2020九年级数学上册 第1章 二次函数 1

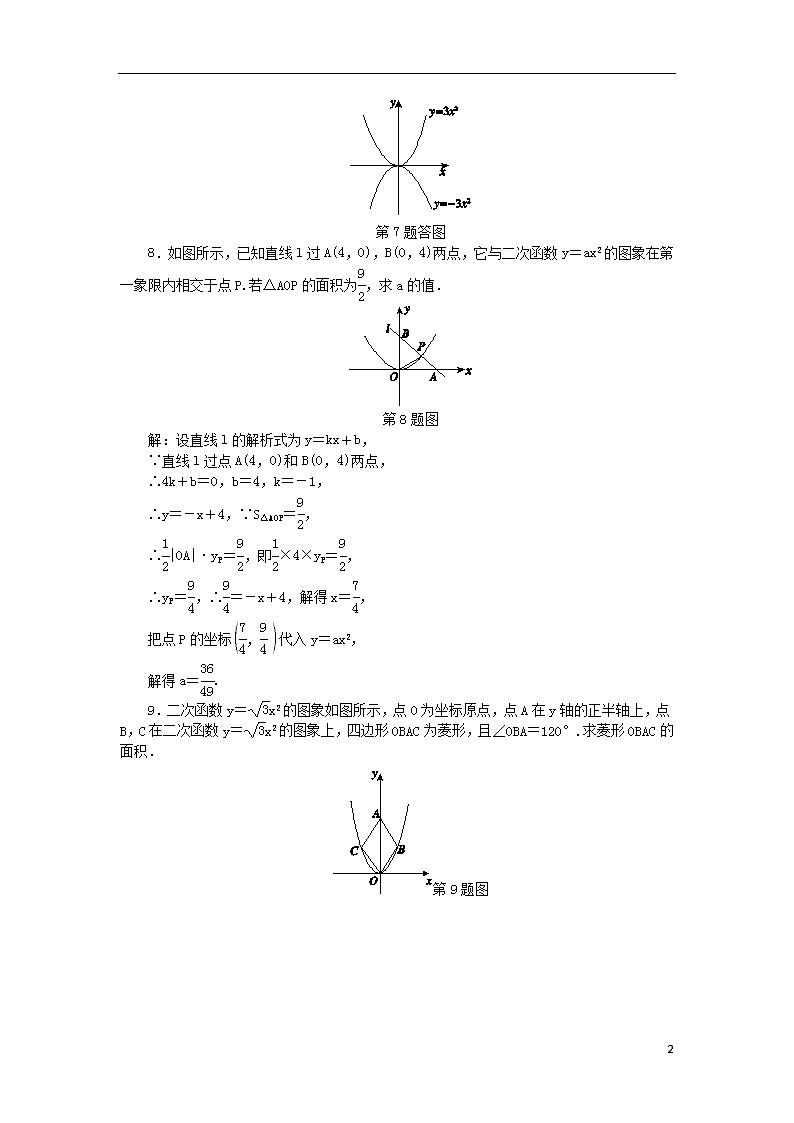
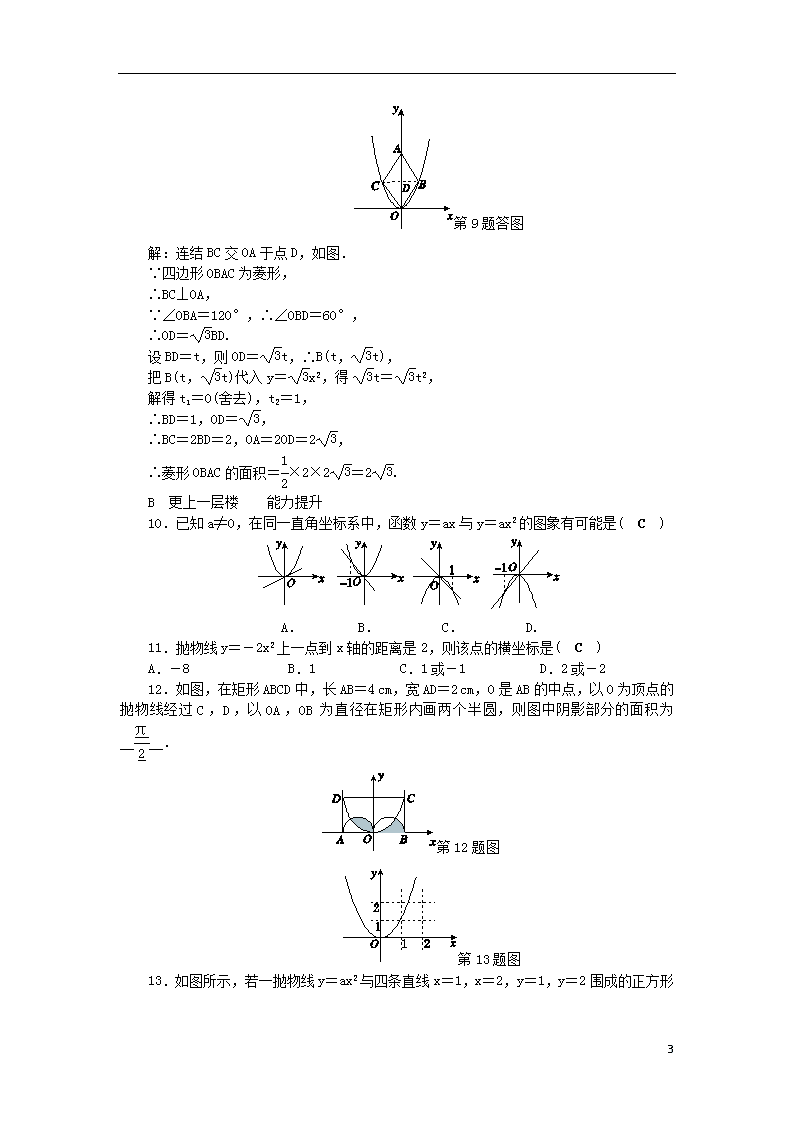
1.2 二次函数的图象(1)‎ ‎(见B本1页)‎ A　练就好基础　基础达标 ‎1．若二次函数y＝ax2的图象过点P(－2，4)，则该图象必经过点(　A　)‎ A．(2，4)　　　　　　　 B．(－2，－4)‎ C．(4，2) D．(4，－2)‎ ‎2．已知抛物线y＝(1－m)x2，除顶点外，其余各点均在x轴的下方，则m的取值范围为(　C　)‎ A．m＝1　 B．m<‎1　‎ C．m>1　 D．m<0‎ ‎3．关于y＝x2，y＝x2，y＝3x2的图象， 下列说法中不正确的是(　C　)‎ A．顶点相同 B．对称轴相同 C．图象形状相同 D．最低点相同 ‎4．河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y＝－x2.当水面离桥拱顶的高度DO是‎4 m时，水面宽度AB为(　C　)‎ 第4题图 A．－‎20 m B．‎10 m C．‎20 m D．－‎‎10 m ‎5．函数y＝－3x2的图象是__抛物线__，它关于__y轴__对称，开口__向下__，顶点坐标是　(0，0)　，顶点是抛物线的最__高__点．‎ ‎6．有下列四个二次函数：①y＝x2；②y＝－2x2；③y＝x2；④y＝3x2.其中抛物线相对开口从大到小的排列顺序是__③①②④__．(填序号)‎ ‎7．在同一直角坐标系中作出y＝3x2和y＝－3x2的图象，并比较两者的异同．‎ 解：如图所示：两图象开口大小、形状相同，但是开口方向不同．‎ 5‎ 第7题答图 ‎8．如图所示，已知直线l过A(4，0)，B(0，4)两点，它与二次函数y＝ax2的图象在第一象限内相交于点P.若△AOP的面积为，求a的值．‎ 第8题图 解：设直线l的解析式为y＝kx＋b，‎ ‎∵直线l过点A(4，0)和B(0，4)两点，‎ ‎∴4k＋b＝0，b＝4，k＝－1，‎ ‎∴y＝－x＋4，∵S△AOP＝，‎ ‎∴|OA|·yP＝，即×4×yP＝，‎ ‎∴yP＝，∴＝－x＋4，解得x＝，‎ 把点P的坐标代入y＝ax2，‎ 解得a＝.‎ ‎9．二次函数y＝x2的图象如图所示，点O为坐标原点，点A在y轴的正半轴上，点B，C在二次函数y＝x2的图象上，四边形OBAC为菱形，且∠OBA＝120°.求菱形OBAC的面积．‎ 第9题图 5‎ ‎　　　　第9题答图 解：连结BC交OA于点D，如图．‎ ‎∵四边形OBAC为菱形，‎ ‎∴BC⊥OA，‎ ‎∵∠OBA＝120°，∴∠OBD＝60°，‎ ‎∴OD＝BD.‎ 设BD＝t，则OD＝t，∴B(t，t)，‎ 把B(t，t)代入y＝x2，得t＝t2，‎ 解得t1＝0(舍去)，t2＝1，‎ ‎∴BD＝1，OD＝，‎ ‎∴BC＝2BD＝2，OA＝2OD＝2，‎ ‎∴菱形OBAC的面积＝×2×2＝2.‎ B　更上一层楼　　能力提升 ‎10．已知a≠0，在同一直角坐标系中，函数y＝ax与y＝ax2的图象有可能是(　C　)‎ A．　　　　B．　 　　　C．　　　 　D.‎ ‎11．抛物线y＝－2x2上一点到x轴的距离是2，则该点的横坐标是(　C　)‎ A．－8 B．‎1 ‎ C．1或－1 D．2或－2‎ ‎12．如图，在矩形ABCD中，长AB＝‎4 cm，宽AD＝‎2 cm，O是AB的中点，以O为顶点的抛物线经过C，D，以OA，OB为直径在矩形内画两个半圆，则图中阴影部分的面积为____．‎ 第12题图 ‎　　　第13题图 ‎13．如图所示，若一抛物线y＝ax2与四条直线x＝1，x＝2，y＝1，y＝2围成的 5‎ 正方形有公共点，则a的取值范围为__≤a≤2__．‎ 第14题图 ‎14．有一座抛物线形拱桥，其水面宽AB为‎18 m，拱顶O到水面AB的距离OM为‎8 m，货船在水面上的部分的横截面是矩形CDEF，如图所示建立直角坐标系．‎ ‎(1)求此抛物线的解析式；‎ ‎(2)如果限定矩形的长CD为‎9 m，那么矩形的宽DE不能超过多少米，才能使船通过拱桥？‎ ‎(3)若设EF＝a，请将矩形CDEF的面积S用含a的代数式表示，并指出a的取值范围. ‎ 解：(1)y＝－x2(－9≤x≤9)．‎ ‎(2)∵CD＝9，‎ ‎∴点E的横坐标为，则点E的纵坐标为－×＝－2，‎ ‎∴点E的坐标为，‎ 因此要使货船通过拱桥，货船最大高度不能超过8－2＝6(米)．‎ ‎(3)由于EF＝a，则E点坐标为，‎ 此时ED＝8－＝8－a2，‎ ‎∴S矩形CDEF＝EF·ED＝8a－a3(0＜a＜18)．‎ C　开拓新思路　拓展创新 第15题图 ‎15．二次函数y＝x2的图象如图所示，点A0位于坐标原点，A1，A2，A3，…，A2018在y轴的正半轴上，B1，B2，B3，…，B2018在二次函数y＝x2第一象限的图象上．若△A0B‎1A1，△A1B‎2A2, △A2B‎3A3，…，△A2017B‎2018A2018都为等边三角形，则△A0B‎1A1的边长是__1__；△A2B‎3A3的边长是__3__；△A2017B‎2018A2018的边长是__2018__．‎ 5‎ 第16题图 ‎16．如图所示，抛物线①y＝x2和②y＝－x2.在x轴上有动点P，从原点出发，以每秒2 (cm)的速度沿x轴正方向运动，出发t (s)后，过P点作与y轴平行的直线交①于点A，交②于点B，过A，B分别作x轴的平行线交①于点D，交②于点C.‎ ‎(1)求点B、点D的坐标(用含t的式子表示)；‎ ‎(2)点P运动几秒时，四边形ABCD为正方形？‎ 第16题答图 解：(1)如图，P点坐标为(2t，0)，代入y＝－x2，可求B点坐标为B(2t，－2t2)，‎ P点关于y轴的对称点为P′(－2t，0)，‎ 代入y＝x2可求D点坐标为D(－2t，4t2)．‎ ‎(2)由题意知四边形ABCD为矩形，‎ 当AD＝AB时，四边形ABCD为正方形，‎ 即2t－(－2t)＝4t2－(－2t2)，‎ ‎6t2＝4t，解得t＝或t＝0(舍去)．‎ 即点P运动秒时，四边形ABCD为正方形．‎ 5‎