- 2021-11-11 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学下册 二次函数的图象与性质
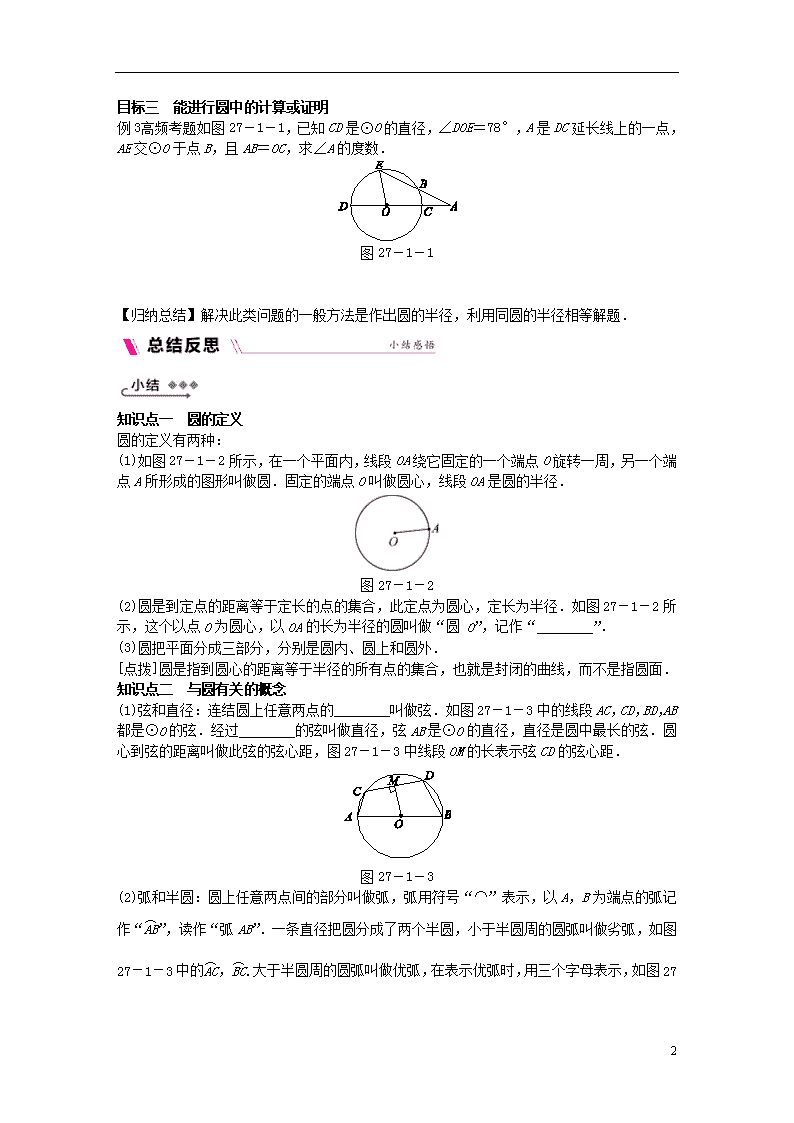
27.1.1 圆的基本元素 知|识|目|标 1.通过画圆和表示圆,知道圆的定义以及同心圆、等圆等概念. 2.在阅读教材、动手实践、类比思考、例题辨析的基础上,弄清弧、弦、圆心、半径、直径等概念. 3.经历对圆的半径、直径的数量关系的自主探究过程,能计算或证明圆中角或线段的数量关系等. 目标一 能画出符合条件的圆 例1 教材补充例题 画出符合下列条件的圆: (1)画3个以点O为圆心的圆;(2)画3个以0.7厘米为半径的圆;(3)画出以点A为圆心,0.7厘米为半径的圆;(4)画一条线段AB,再以AB的中点为圆心,AB长为半径画圆. 【归纳总结】圆的分类: (1)在同一平面内,圆心相同而半径不同的圆叫做同心圆;(2)半径相等的两个圆称为等圆;(3)圆的位置由圆心确定,圆的大小由半径的长度确定. 目标二 理解圆的相关概念 例2 教材补充例题 有以下命题:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的两条弧是等弧;⑥经过圆内一定点的弦有无数条;⑦经过圆内一定点的直径有无数条;⑧等圆的半径相等;⑨弧分为优弧和劣弧;⑩圆心相同而半径不同的两个圆叫做同心圆.其中正确的有( ) A.6个 B.7个 C.8个 D.9个 【归纳总结】圆中容易混淆的“两组基本概念”: 1.弦与直径. (1)直径是弦,是圆中最长的弦,但弦不一定是直径; (2)弦是连结圆上任意两点的线段,而直径是经过圆心的弦. 2.弧与半圆. (1)半圆是弧,但弧不一定是半圆; (2)圆上任意两点把圆分成两条弧,圆上任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆. 4 目标三 能进行圆中的计算或证明 例3 高频考题 如图27-1-1,已知CD是⊙O的直径,∠DOE=78°,A是DC延长线上的一点,AE交⊙O于点B,且AB=OC,求∠A的度数. 图27-1-1 【归纳总结】解决此类问题的一般方法是作出圆的半径,利用同圆的半径相等解题. 知识点一 圆的定义 圆的定义有两种: (1)如图27-1-2所示,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.固定的端点O叫做圆心,线段OA是圆的半径. 图27-1-2 (2)圆是到定点的距离等于定长的点的集合,此定点为圆心,定长为半径.如图27-1-2所示,这个以点O为圆心,以OA的长为半径的圆叫做“圆 O”,记作“________”. (3)圆把平面分成三部分,分别是圆内、圆上和圆外. [点拨]圆是指到圆心的距离等于半径的所有点的集合,也就是封闭的曲线,而不是指圆面. 知识点二 与圆有关的概念 (1)弦和直径:连结圆上任意两点的________叫做弦.如图27-1-3中的线段AC,CD,BD,AB都是⊙O的弦.经过________的弦叫做直径,弦AB是⊙O的直径,直径是圆中最长的弦.圆心到弦的距离叫做此弦的弦心距,图27-1-3中线段OM的长表示弦CD的弦心距. 图27-1-3 (2)弧和半圆:圆上任意两点间的部分叫做弧,弧用符号“⌒”表示,以A,B为端点的弧记作“”,读作“弧AB”.一条直径把圆分成了两个半圆,小于半圆周的圆弧叫做劣弧,如图27-1-3中的,.大于半圆周的圆弧叫做优弧,在表示优弧时,用三个字母表示,如图27-1- 4 3中的. [点拨]等弧是指能够互相重合的弧,等弧只能在同圆或等圆中出现. 已知在半径为5的⊙O中,弦AB=5 ,弦AC=5,求∠BAC的度数. 解:如图27-1-4,连结OA,OB,OC. ∵AC=OA=OC=5, ∴△OAC是等边三角形, ∴∠OAC=60°. ∵OA2+OB2=52+52=50,AB2=(5 )2=50, ∴OA2+OB2=AB2, 图27-1-4 ∴△OAB是直角三角形. 又∵OA=OB, ∴△OAB是等腰直角三角形, ∴∠OAB=45°, ∴∠BAC=∠OAB+∠OAC=45°+60°=105°. 以上解答过程完整吗?若不完整,请进行补充. 4 教师详解详析 【目标突破】 例1 解:根据题目中的条件,分别画出符合条件的圆: 例2 [解析] A ①③④⑥⑧⑩正确. 例3 [解析] 已知∠DOE=78°,与未知角∠A构成了内、外角关系,而∠E也未知,且AB=OC这一条件不能直接使用,因此想到同圆的半径相等,需连结OB,从而得到OB=AB. 解:如图,连结OB. ∵AB=OC,OB=OC, ∴AB=OB, ∴∠A=∠1. 又∵OB=OE, ∴∠E=∠2=∠1+∠A=2∠A, ∴∠DOE=∠E+∠A=3∠A. 又∵∠DOE=78°,∴3∠A=78°,∴∠A=26°. 【总结反思】 [小结] 知识点一 (2)⊙O 知识点二 (1)线段 圆心 [反思] 不完整.补充如下: 若点B,C在直线OA的异侧,则∠BAC=∠OAB+∠OAC=45°+60°=105°; 若点B,C在直线OA的同侧,如图所示, 则∠BAC=∠OAC-∠OAB=60°-45°=15°. 综上可得,∠BAC的度数是105°或15°. 4查看更多