初中数学中考总复习课件PPT：第13课时　二次函数的图象与性质【46张】

初中数学中考总复习课件PPT：第13课时　二次函数的图象与性质【46张】

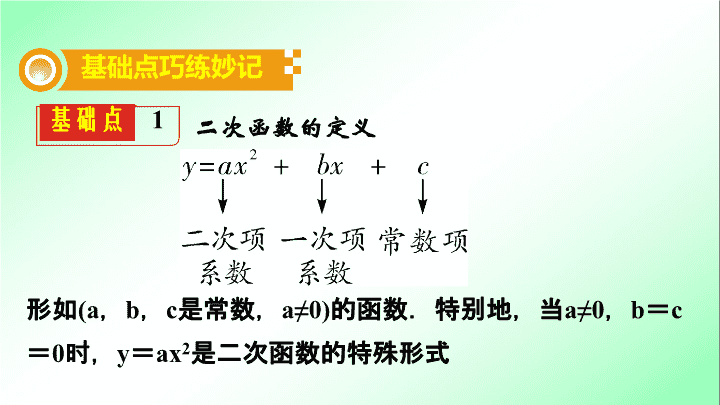
第一部分 夯实基础　提分多 第 三 单元 函数 第1 3 课时 二次函数的图象与性质 基础点 1 二次函数的定义 基础点巧练妙记 形如 (a ， b ， c 是常数， a≠0) 的函数．特别地，当 a≠0 ， b ＝ c ＝ 0 时， y ＝ ax 2 是二次函数的特殊形式 基础点 2 二次函数的图象与性质 1 ． 根据函数解析式判断函数性质及图象 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 性质 对称轴 直接运用公式 x ＝ ① ________ 求解 注：还可利用 x ＝ ( 其中 x 1 、 x 2 为 y 值相等的两个点对应的横坐标 ) 求解 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 性质 顶点坐标 1. 直接运用顶点坐标公式 ② ________________ 求解； 2. 运用配方法将一般式转化为顶点式求解； 3. 将对称轴的 x 值代入函数表达式求得对应 y 值 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 性质 增减性 a >0 时，在对轴左侧， y 随 x 的增大而 ③ ________ ；在对称轴右侧， y 随 x 的增大而 ④ ________ a <0 时，在对称轴 ⑤ ________ ， y 随 x 的增大而增大；在对称轴 ⑥ ______ ， y 随 x 的增大而减小 减小 增大 左侧 右侧 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 性质 最值 a >0 时，当 x ＝ ⑦ ______ 时， y 的最小值为 ； 离对称轴越近的点函数值越小 a <0 时， y 的最大值 为 ⑧ ________ ； 离对称轴越近的点函数值越大 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 图象 a ，决定抛物线开口方向 a ⑨ _____0 开口向上 a <0 开口向下 a ， b 决定抛物线的对称轴位置 b ＝ 0 对称轴为 y 轴 a 、 b 同号 对称轴为 y 轴 ⑩ ____ 侧 a 、 b 异号 对称轴为 y 轴右侧 > 左 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 图象 c ，决定抛物线与 y 轴交点的位置 c ＝ 0 抛物线过原点 c >0 抛物线与 y 轴交于 ⑪ ______ 半轴 c <0 抛物线与 y 轴交于 ⑫ ______ 半轴 正 负 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 函数 图象 b 2 － 4 ac ，决定抛物线与 x 轴交点个数 b 2 － 4 ac ＝ 0 与 x 轴有唯一交点 ( 顶点 ) b 2 － 4 ac >0 与 x 轴有 ⑬ ________ 交点 b 2 － 4 ac <0 与 x 轴没有交点 两个 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 特殊 关系 2 a ＋ b － 与 1 比较 2 a － b － 与－ 1 比较 b 2 － 4 ac 与 x 轴交点个数 二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠0) 判断 特殊 关系 a ＋ b ＋ c 令 x ＝ 1 ，看纵坐标 a － b ＋ c 令 x ＝ － 1 ，看纵坐标 4 a ＋ 2 b ＋ c 令 x ＝ 2 ，看纵坐标 4 a － 2 b ＋ c 令 x ＝－ 2 ，看纵坐标 2 ． 根据函数图象判断相关结论 a ⑭ ____ 0 b ⑮ ____0 c ＜ 0 b 2 － 4 ac ＞ 0 a ⑯ ____0 b ＝ 0 c ＞ 0 b 2 － 4 ac ⑰ ____0 a ＞ 0 b ⑱ ____0 c ⑲ ____0 b 2 － 4 ac ＞ 0 a ＜ 0 b ____0 c ＜ 0 b 2 － 4 ac ____0 ＞ ＞ ＞ ＜ ＜ ＞ = ＞ 20 21 a ＞ 0 b ㉒ ____ 0 c ＞ 0 b 2 - 4 ac ㉓__0 a ㉔ ____ 0 b ＞ 0 c ㉕ ____ 0 b 2 － 4 ac ＞ 0 a ㉖ ____ 0 b ㉗ ____ 0 c ＝ 0 b 2 － 4 ac ＞ 0 a ＞ 0 b ㉘____0 c=0 b 2 － 4 ac ㉙__0 ＞ ＜ ＞ = ＜ ＞ = = 1 ． 表达式的三种形式 (1) 一般式： y ＝ ax 2 ＋ bx ＋ c ( a 、 b 、 c 为常数， a ≠0) ； (2) 顶点式： ____________( a 为常数， a ≠0 ， ( h ， k ) 为顶点坐标 ) ； (3) 交点式： _________________ ( a 为常数， a ≠0 ， x 1 ， x 2 为抛物线与 x 轴交点的横坐标 ) ； 基础点 3 二次函数表达式的确定 y ＝ a ( x － h ) 2 ＋ k y ＝ a ( x － x 1 )( x － x 2 ) 顶点式 一般式 交点式 ，若顶点在原点，可设为 y ＝ ax 2 . 配方 因式分解 (4) 三种表达式之间的关系 2 ． 待定系数法求二次函数的表达式： (1) 对于二次函数 y ＝ ax 2 ＋ bx ＋ c ，若系数 a 、 b 、 c 中有一个未知，则代入任意一点坐标；若有两个未知，则代入任意两点坐标；若三个都未知，根据下表所给的点坐标选择适当的表达式 已知 所设表达式 顶点＋其他点 y ＝ a ( x － h ) 2 ＋ k 与 x 轴的两个交点＋其他点 y ＝ a ( x － x 1 )( x － x 2 ) 与 x 轴的一个交点＋对称轴＋其他点 任意三个点 y ＝ ax 2 ＋ bx ＋ c (2) 联立方程 ( 组 ) ，求得系数或常数项；将所得系数或常数项代入表达式即可． 基础点 4 二次函数图象的平移 (1) 上加下减 ： y ＝ ax 2 ＋ bx ＋ c y ＝ ax 2 ＋ bx ＋ c ＋ m y ＝ ax 2 ＋ bx ＋ c ＋ n 向上平移 m 个单位 向下平移 m 个单位 (2) 左加右减 ： 方法一： y ＝ ax 2 ＋ bx ＋ c 化为 y ＝ a （ x - h ） 2 ＋ k 规律： 向右平移 m 个单位 y ＝ a （ x - h-m ） 2 ＋ k 向左平移 m 个单位 y ＝ a （ x - h+m ） 2 ＋ k 左 + 右 - 方法二： y ＝ ax 2 ＋ bx ＋ c 左右平移时，给每一个 x 都加 m 或减 m . 向左平移 m 个单位 规律： 向右平移 m 个单位 y ＝ a （ x+m ） 2 ＋ b(x ＋ m) ＋ c y ＝ a （ x - m ） 2 ＋ b(x － m) ＋ c 左 + 右 - 基础点 5 二次函数与一元二次方程、不等式的关系 1 ． 二次函数与一元二次方程的关系 (1) 抛物线与 x 轴有两个交点 ⇔ b 2 － 4 ac ＞ 0 ⇔ 方程 ax 2 ＋ bx ＋ c ＝ 0 有两个不相等的实数根； (2) 抛物线与 x 轴有一个交点 ⇔ b 2 － 4 ac ＝ 0 ⇔ 方程 ax 2 ＋ bx ＋ c ＝ 0 有两个相等的实数根； (3) 抛物线与 x 轴无交点 ⇔ b 2 － 4 ac ＜ 0 ⇔ 方程 ax 2 ＋ bx ＋ c ＝ 0 无实数根． 2. 二次函数与不等式的关系 (1) ax 2 ＋ bx ＋ c >0 的解集 ⇔ 函数 y ＝ ax 2 ＋ bx ＋ c 的图象位于 x 轴上方对应的点的横坐标的取值范围； (2 )ax 2 ＋ bx ＋ c <0 的解集 ⇔ 函数 y ＝ ax 2 ＋ bx ＋ c 的图象位于 x 轴下方对应的点的横坐标的取值范围．            练 提 分 必 抛物线 y ＝ x 2 ＋ 6 x ＋ 8 与 x 轴交点坐标为 ______________________ ； 当 x 2 ＋ 6 x ＋ 8 ＝ 0 时， x 的值为 ________ ； 当 x 2 ＋ 6 x ＋ 8>0 时， x 的取值范围为 _____________ ； x 2 ＋ 6 x ＋ 8<0 时， x 的取值范围为 ___________ ． ( － 2 ， 0) 或 ( － 4 ， 0) － 2 或－ 4 x < － 4 或 x > － 2 － 4< x < － 2 例 1 　在探究二次函数图象性质的过程中， x 与 y 的对应值如下表： 重难点精讲优练 类型 1 二次函数的顶点坐标、对称轴与增减性 x … － 1 0 1 2 3 … y … 0 － 3 － 4 － 3 0 … (1) 表中二次函数表达式为 ______________ ； (2) 函数图象开口向 ________ ，顶点坐标为 ________ ，对称轴为 ________ ； (3) 当 x ＝ ____ 时，函数取最小值，最小值为 ________ ； x … － 1 0 1 2 3 … y … 0 － 3 － 4 － 3 0 … y ＝ x 2 － 2 x － 3 上 (1 ，－ 4) x ＝ 1 1 － 4 (4) 函数图象与 y 轴交点坐标为 __________ ，与 x 轴交点坐标为 _________________ ； (5) 画出此函数图象； (0 ，－ 3) ( － 1 ， 0) ， (3 ， 0) 例 1 题图 例 1 题解图 (6) 根据图象回答： x 取何值时， y ＞ 0 ； x 取何值时， y ＜ 0 ； x 取何值时， y 随 x 的增大而增大； x 取何值时， y 随 x 的增大而减小？ 当 x ＜－ 1 或 x ＞ 3 时， y ＞ 0 ；当－ 1 ＜ x ＜ 3 时， y ＜ 0 ；当 x ＞ 1 时， y 随 x 的增大而增大；当 x ＜ 1 时， y 随 x 的增大而减小． 练习 1 　已知：抛物线 y ＝ x 2 － 3kx ＋ 2k ＋ . (1) 当顶点在 y 轴上时， k 的值为 ________ ； (2) 当顶点在 x 轴上时， k 的值为 ________ ； (3) 当函数图象经过原点时， k 的值为 ________ ； (4) 当函数图象与 x 轴的两个交点在 y 轴的两侧时， k 的取值范围为 ________ ． 0 解法提示： (1)∵ 抛物线 y ＝ x 2 － 3 kx ＋ 2 k ＋ 顶点在 y 轴上， ∴ － 3 k ＝ 0 ，解得 k ＝ 0 ； (2)∵ 抛物线 y ＝ x 2 － 3 kx ＋ 2 k ＋ 在 x 轴上， ∴ b 2 － 4 ac ＝ 0 ， ∴ ( － 3 k ) 2 － 4 × 1 × (2 k ＋ ) ＝ 0 ， 解得 k ＝ 1 或 k ＝－ ； (3) 抛物线 y ＝ x 2 － 3 kx ＋ 2 k ＋ 经过原点， ∴ 2 k ＋ ＝ 0 ，解得 x ＝－ ； (4) 设抛物线 y ＝ x 2 － 3 kx ＋ 2 k ＋ 的两个交点坐标为 ( x 1 ， 0) ， ( x 2 ， 0) ， ∵ 抛物线与 x 轴的两个交点在 y 轴的两侧 ， ∴ x 1 x 2 ＜ 0 ， ∴ x 1 x 2 ＝ ＝ ＜ 0 ， 即 k ＜－ . 变式拓展 　已知：二次函数 y ＝ x 2 ＋ bx ＋ c ( b ， c 为常数 ) ． (1) 当 b ＝ 2 ， c ＝－ 3 时，求二次函数的最小值； (2) 当 c ＝ b 2 时，若在自变量 x 的值满足 b ≤ x ≤ b ＋ 3 的情况下，与其对应的函数值 y 的最小值为 21 ，求此时二次函数的解析式． 解： (1) 当 b ＝ 2 ， c ＝－ 3 时，二次函数的解析式为 y ＝ x 2 ＋ 2 x － 3 ，即 y ＝ ( x ＋ 1) 2 － 4 ， ∴当 x ＝－ 1 时，二次函数取得最小值－ 4 ； (2) 当 c ＝ b 2 时，二次函数的解析式为 y ＝ x 2 ＋ bx ＋ b 2 ，其图象是开口向上，对称轴为 x ＝－ 的抛物线， ①若－ ＜ b ，即 b ＞ 0 ， ∴当 b ≤ x ≤b ＋ 3 时， y 随 x 的增大而增大， ∴当 x ＝ b 时， y 最小值 ＝ b 2 ＋ b · b ＋ b 2 ＝ 3 b 2 ， ∴ 3 b 2 ＝ 21 ，解得 b 1 ＝－ ( 舍 ) ， b 2 ＝ . ∴ 二次函数解析式为 y ＝ x 2 ＋ x ＋ 7 ； ②若 b ≤ － ≤ b ＋ 3 ，即－ 2≤ b ≤0 ， ∴当 x ＝－ 时， y 最小值 ＝ ( － ) 2 ＋ b ·( － ) ＋ b 2 ＝ b 2 ， ∴ b 2 ＝ 21 ，解得 b 1 ＝－ 2 ( 舍 ) ， b 2 ＝ 2 ( 舍 ) ； ③若－ ＞ b ＋ 3 ，即 b ＜ -2 ∴当 b ≤ x ≤ b ＋ 3 时， y 随 x 的增大而减小， ∴当 x ＝ b ＋ 3 时， y 最小值 ＝ ( b ＋ 3) 2 ＋ b ( b ＋ 3) ＋ b 2 ＝ 3 b 2 ＋ 9 b ＋ 9 ，∴ 3 b 2 ＋ 9 b ＋ 9 ＝ 21 ，即 b 2 ＋ 3 b － 4 ＝ 0 ，解得 b 1 ＝ 1( 舍 ) ， b 2 ＝－ 4 ，∴二次函数解析式为 y ＝ x 2 － 4 x ＋ 16 ， 综上所述， b ＝ 或 b ＝－ 4 ， ∴此时二次函数的解析式为 y ＝ x 2 ＋ x ＋ 7 或 y ＝ x 2 － 4 x ＋ 16. 类型 2 二次函数图象与系数 a 、 b 、 c 的关系 例 2 题图 C 例 2 　已知二次函数 y ＝ ax 2 ＋ bx ＋ c ( a ≠ 0) 的图象如图所示，给出以下四个结论： ① abc ＜ 0 ； ② a ＋ b ＋ c ＜ 0 ； ③ 4 a ＋ c ＞ 2 b ； ④ 2 a － b ＝ 0 ； ⑤ m ( am ＋ b ) ＋ b ＜ a ( m ≠ － 1) ，其中，正确结论的个数为 ( 　　 ) A . 2 个 B . 3 个 C . 4 个 D . 5 个 【 解析 】 ∵ 抛物线开口向下，∴ a ＜ 0 ，∵抛物线的对称轴为直线 x ＝－ ＝－ 1 ＜ 0 ，∴ b ＝ 2 a ，∴ b ＜ 0 ，∵抛物线与 y 轴的交点在 x 轴上方，∴ c ＞ 0 ，∴ abc ＞ 0 ，∴①错误；∵ x ＝ 1 时， y ＜ 0 ，∴ a ＋ b ＋ c ＜ 0 ，∴②正确；∵抛物线的对称轴为直线 x ＝－ 1 ，抛物线与 x 轴的一个交点在点 (0 ， 0) 和 (1 ， 0) 之间，∴抛物线与 x 轴的另一个交点在点 ( － 3 ， 0) 和 ( － 2 ， 0) 之间，∴当 x ＝－ 2 时， y ＞ 0 ，∴ 4 a － 2 b ＋ c ＞ 0 ，∴③正确；∵抛物线对称轴 x ＝－ ＝－ 1.∴ b ＝ 2 a ，即 2 a － b ＝ 0 ，∴④正确；∵抛物线的对称轴为直线 x ＝－ 1 ，∴当 x ＝－ 1 时， y 有最大值，∴ am 2 ＋ bm ＋ c ＜ a － b ＋ c ( m ≠ － 1) ，∴ m ( am ＋ b ) ＜ a － b ( m ≠ － 1) ，∴⑤正确；综上所述，正确的结论有②③④⑤ . A 练习 2 　已知二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象与 x 轴交于点 ( － 2 ， 0) 、 ( x 2 ， 0) ，且 1 ＜ x 2 ＜ 2 ，与 y 轴正半轴的交点在 (0 ， 2) 下方，在下列结论中：① b ＜ 0 ，② 4 a － 2 b ＋ c ＝ 0 ，③ 2 a － b ＋ 1 ＜ 0 ，④ b ＜ a ＜ c . 其中，正确的结论是 ( 　　 ) A . ①② B . ③④ C . ①②③ D . ①②④ 【 解析 】 画出图象如解图， ∵开口向下，∴ a ＜0，∵ x ＝－ ＜0，∴ b ＜0，∴①正确；根据二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象与 x 轴交于点(－2，0)、( x 2 ，0)，且1＜ x 2 ＜2，与 y 轴的正半轴的交点在(0，2)的下方，把 x ＝－2代入得：4 a －2 b ＋ c ＝0，∴②正确；由4 a －2 b ＋ c ＝0得2 a － b ＝－ 例 2 题解图 而0＜ c ＜2，∴－1＜－ ＜0，∴－1＜2 a － b ＜0，∴2 a － b ＋1＞0，∴③错误；∵图象与 x 轴两交点为(－2，0)，( x 2 ，0)，且1＜ x 2 ＜2，对称轴x＝－ ＝－ ，则对称轴－ ＜－ ＜0，且 a ＜0，∴－ a ＞－ b ，∴a＜ b ＜0，由抛物线与 y 轴的正半轴的交点在(0，2)的下方，得 c ＞0，即 a ＜ b ＜c，∴④错误；∴正确的结论为①②. 类型 3 二次函数与一元二次方程的关系 例 3 　已知抛物线 y ＝ ( x － m ) 2 － ( x － m ) ，其中 m 是常数． (1) 求证：不论 m 为何值，该抛物线与 x 轴一定有两个公共点； (2) 若该抛物线的对称轴为直线 x ＝ . ① 求该抛物线的函数解析式； ② 把该抛物线沿 y 轴向上平移多少个单位长度后，得到的抛物线与 x 轴只有一个公共点 【 自主解答 】 (1) 证明 ： ∵ y ＝ ( x － m ) 2 － ( x － m ) ＝ x 2 － (2 m ＋ 1)x ＋ m 2 ＋ m ， ∴ b 2 － 4 ac ＝ [ － (2 m ＋ 1)] 2 － 4×1×( m 2 ＋ m ) ＝ 4 m 2 ＋ 4 m ＋ 1 － 4 m 2 － 4 m ＝ 1 ＞ 0 ， ∴不论 m 为何值，该抛物线与 x 轴一定有两个公共点； (2) 解：①∵ y ＝ x 2 － (2 m ＋ 1)x ＋ m 2 ＋ m 的对称轴为直线 x ＝－ ＝ ， 抛物线对称轴为直线 x ＝ ， ∴ ＝ ， 解得 m ＝ 2 ， ∴抛物线解析式为 y ＝ x 2 － 5 x ＋ 6 ； ②设抛物线沿 y 轴向上平移 k 个单位长度后，得到的抛物线与 x 轴只有一个公共点，则平移后抛物线的解析式为 y ＝ x 2 － 5 x ＋ 6 ＋ k . ∵ 抛物线 y ＝ x 2 － 5 x ＋ 6 ＋ k 与 x 轴只有一个公共点， ∴ Δ ＝ 5 2 － 4(6 ＋ k ) ＝ 0 ， ∴ k ＝ ， 即把该抛物线沿 y 轴向上平移 个单位长度后，得到的抛物线与 x 轴只有一个公共点． 练习 3 　 (2017 张家界节选 ) 已知抛物线 c 1 的顶点为 A ( － 1 ， 4) ，与 y 轴的交点为 D (0 ， 3) ． (1) 求 c 1 的解析式； (2) 若直线 l 1 ： y ＝ x ＋ m 与 c 1 仅有唯一的交点，求 m 的值； (3) 若抛物线 c 1 关于 y 轴对称的抛物线记作 c 2 ，平行于 x 轴的直线记作 l 2 ： y ＝ n . 试结合图形回答：当 n 为何值时， l 2 与 c 1 和 c 2 共有：①两个交点；②三个交点；③四个交点． 解 ： (1)∵ 抛物线 c 1 的顶点为 A ( － 1 ， 4) ， ∴设抛物线 c 1 的解析式为 y ＝ a ( x ＋ 1) 2 ＋ 4 ， ∵点 D (0 ， 3) 在抛物线上， ∴ a (0 ＋ 1) 2 ＋ 4 ＝ 3 ， ∴ a ＝－ 1 ， 则抛物线 c 1 的解析式为 y ＝－ ( x ＋ 1) 2 ＋ 4 ， 即 y ＝－ x 2 － 2 x ＋ 3 ； (2) 由题意可得， 即 x 2 ＋ 3 x ＋ m － 3 ＝ 0 ， ∵直线与抛物线仅有唯一的交点， ∴ b 2 － 4 ac ＝ 9 － 4( m － 3) ＝ 0 ，解得 m ＝ ； (3) 根据题意可得抛物线 c 1 ： y ＝－ ( x ＋ 1) 2 ＋ 4 关于 y 轴对称的抛物线 c 2 的解析式为： y ＝－ ( x － 1) 2 ＋ 4. ① 由图象可得当 n ＝ 4 时，直线 y ＝ 4 经过两抛物线顶点 ( － 1 ， 4) ， (1 ， 4) ，此时直线 y ＝ 4 与抛物线有两个交点； ②当 n ＝ 3 时，直线 y ＝ 3 ，经过两抛物线的交点 D (0 ， 3) ，此时直线 y ＝ 3 与抛物线有三个交点； ③当 n ＜ 3 或 3 ＜ n ＜ 4 时，直线 y ＝ n 与抛物线有四个交点．