2020九年级数学下册二次函数的图象与性质

2020九年级数学下册二次函数的图象与性质

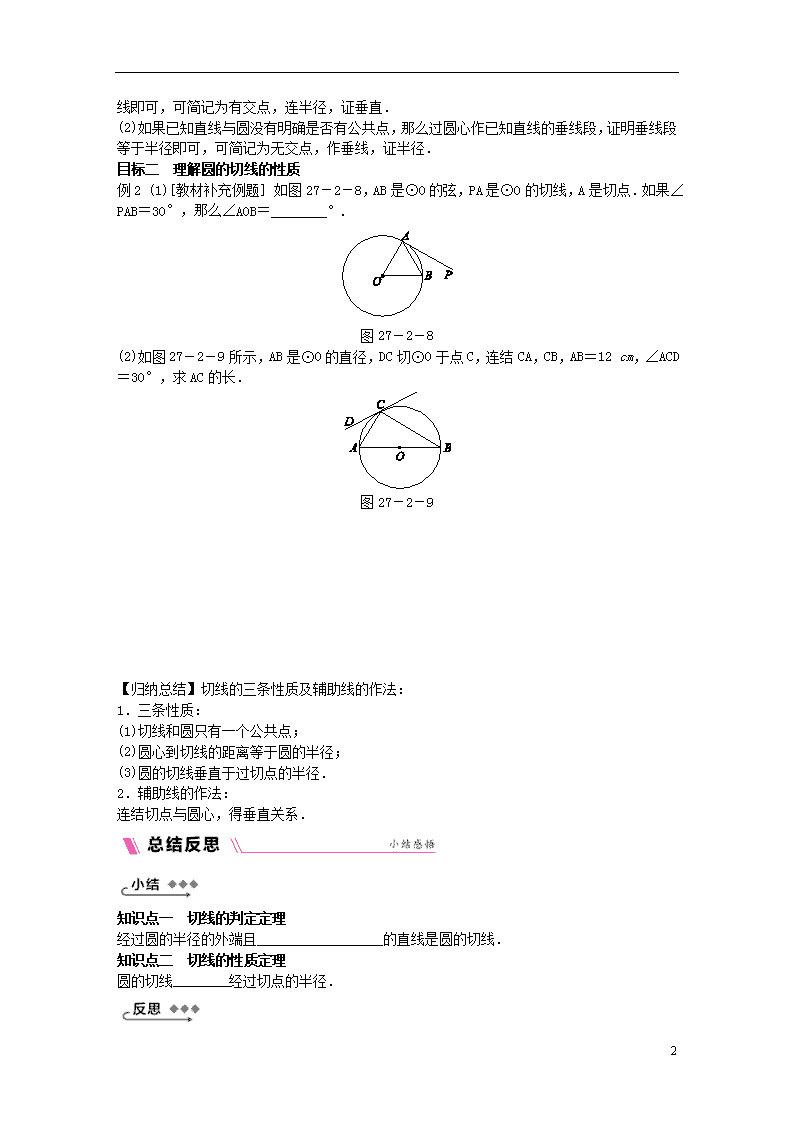
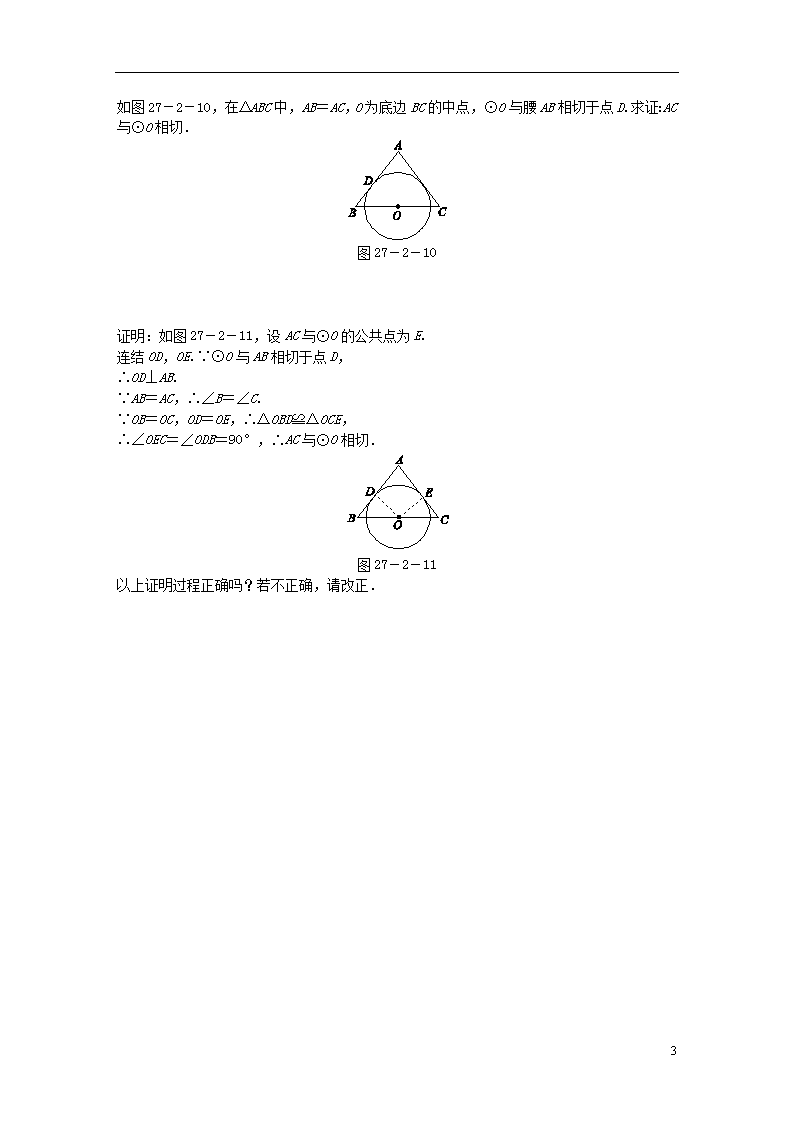
‎27.2.3 切线 第1课时　切线的判定与性质 知|识|目|标 ‎1．通过画图、探究，总结切线的判定方法，能判断一条直线是不是圆的切线．‎ ‎2．通过辨析、思考，能准确理解圆的切线的性质．‎ 目标一　能判断一条直线是不是圆的切线 例1 教材例2针对训练 已知：如图27－2－7，AD是⊙O的直径，直线BC经过点D，并且AB＝AC，∠BAD＝∠CAD.‎ 求证：直线BC是⊙O的切线．‎ 图27－2－7‎ ‎【归纳总结】‎ ‎1．判定圆的切线的“三种方法”：‎ ‎(1)定义法：和圆有且只有一个公共点的直线是圆的切线．‎ ‎(2)求值法(d＝r)：圆心到直线的距离等于半径的直线是圆的切线．‎ ‎(3)判定定理：经过圆的半径的外端且垂直于这条半径的直线是圆的切线．‎ ‎2．判定圆的切线常作的辅助线：‎ ‎(1)‎ 4‎ 如果已知直线过圆上一点，那么连结这点和圆心，得到半径，证明这条半径垂直于已知直线即可，可简记为有交点，连半径，证垂直．‎ ‎(2)如果已知直线与圆没有明确是否有公共点，那么过圆心作已知直线的垂线段，证明垂线段等于半径即可，可简记为无交点，作垂线，证半径．‎ 目标二　理解圆的切线的性质 例2 (1)[教材补充例题] 如图27－2－8，AB是⊙O的弦，PA是⊙O的切线，A是切点．如果∠PAB＝30°，那么∠AOB＝________°.‎ 图27－2－8‎ ‎(2)如图27－2－9所示，AB是⊙O的直径，DC切⊙O于点C，连结CA，CB，AB＝‎12 cm，∠ACD＝30°，求AC的长．‎ 图27－2－9‎ ‎【归纳总结】切线的三条性质及辅助线的作法：‎ ‎1．三条性质：‎ ‎(1)切线和圆只有一个公共点；‎ ‎(2)圆心到切线的距离等于圆的半径；‎ ‎(3)圆的切线垂直于过切点的半径．‎ ‎2．辅助线的作法：‎ 连结切点与圆心，得垂直关系．‎ 知识点一　切线的判定定理 经过圆的半径的外端且__________________的直线是圆的切线．‎ 知识点二　切线的性质定理 圆的切线________经过切点的半径．‎ 4‎ 如图27－2－10，在△ABC中，AB＝AC，O为底边BC的中点，⊙O与腰AB相切于点D.求证：AC与⊙O相切．‎ 图27－2－10‎ ‎　　　‎ 证明：如图27－2－11，设AC与⊙O的公共点为E.‎ 连结OD，OE.∵⊙O与AB相切于点D，‎ ‎∴OD⊥AB.‎ ‎∵AB＝AC，∴∠B＝∠C.‎ ‎∵OB＝OC，OD＝OE，∴△OBD≌△OCE，‎ ‎∴∠OEC＝∠ODB＝90°，∴AC与⊙O相切．‎ 图27－2－11‎ 以上证明过程正确吗？若不正确，请改正．‎ 4‎ 教师详解详析 ‎【目标突破】‎ 例1　证明：∵AB＝AC(已知)，‎ ‎∴△ABC是等腰三角形．‎ ‎∵∠BAD＝∠CAD，‎ ‎∴AD⊥BC，即OD⊥BC.‎ 又∵OD是⊙O的半径，且BC经过点D，‎ ‎∴直线BC是⊙O的切线(切线的判定定理)．‎ 例2　(1)[答案] 60‎ ‎[解析] 由于△OAB为等腰三角形，要求∠AOB，只需求出∠OAB.因为PA是⊙O的切线，所以∠OAB＋∠PAB＝90°，则∠OAB＝90°－30°＝60°，所以△OAB为等边三角形，所以∠AOB＝60°.‎ ‎(2)解：连结OC.因为DC是⊙O的切线，所以OC⊥DC，而∠ACD＝30°，所以∠ACO＝60°.又因为OA＝OC，所以△AOC是等边三角形，所以AC＝OA＝AB＝×12＝6(cm)．‎ ‎【总结反思】‎ ‎[小结] 知识点一　垂直于这条半径 知识点二　垂直于 ‎[反思] 不正确．改正如下：‎ 过点O作OE⊥AC于点E，连结AO，DO.‎ ‎∵AB＝AC，O是BC的中点，‎ ‎∴AO平分∠BAC.‎ 又∵AB与⊙O相切，∴OD⊥AB，‎ ‎∴OD＝OE，∴AC与⊙O相切．‎ 4‎