人教版九年级上册数学同步课件-第24章-24直线和圆的位置关系

人教版九年级上册数学同步课件-第24章-24直线和圆的位置关系

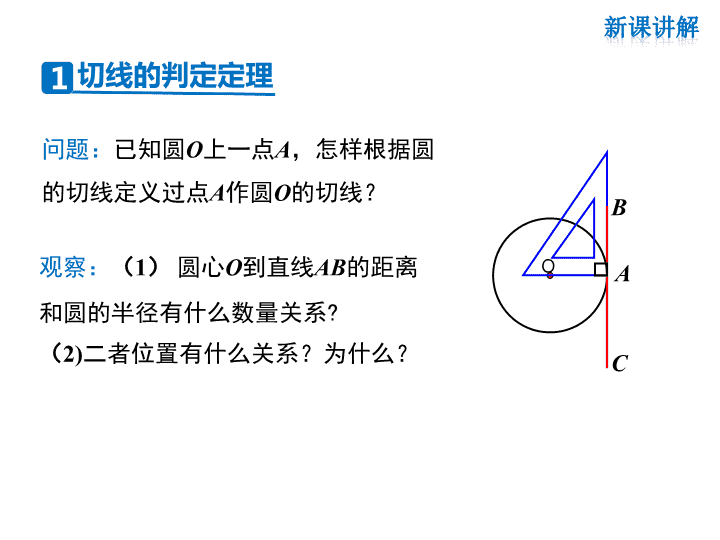
24.2 直线和圆的位置关系 第2课时 切线的性质与判定 第二十四章 圆 砂轮上打磨工件时飞出的火星 右图中让你感受到 了直线与圆的哪种 位置关系？ Ｏ A B C 问题：已知圆O上一点A，怎样根据圆 的切线定义过点A作圆O的切线？ 观察：（1） 圆心O到直线AB的距离 和圆的半径有什么数量关系? （2)二者位置有什么关系？为什么？ 切线的判定定理1 经过半径的外端并且垂直于这 条半径的直线是圆的切线. Ｏ A B C ★切线的判定定理 ★应用格式 判一判： 下列各直线是不是圆的切线？如果不是，请说明为什么？ O. l A O. l A B A O l (1) (2) (3) (1)不是，因为 没有垂直. (2),(3)不是，因为没有经过半径 的外端点A. 注意：在此定理中，“经过半径的外端”和“垂直 于这条半径”，两个条件缺一不可，否则就不是圆的 切线. 判断一条直线是一个圆的切线有三种方法： 1.定义法：直线和圆只有一个公共 点时，我们说这条直线是圆的切线; 2.数量关系法：圆心到这条直线的 距离等于半径(即d=r)时，直线与 圆相切； 3.判定定理：经过半径的外端并且垂 直于这条半径的直线是圆的切线。 l A l O l r d 已知：直线AB经过⊙ O上的点C，并且OA=OB， CA=CB.求证：直线AB是⊙ O的切线. 分析：由于AB过⊙ O上的点C，所以连接OC， 只要证明AB⊥OC即可. 证明：连接OC(如图). ∵ OA＝OB,CA＝CB, ∴ OC是等腰三角形OAB底边AB上的中线.　 ∴ AB⊥OC. ∵ OC是⊙ O的半径, ∴ AB是⊙ O的切线. 例1 如图,△ABC 中，AB ＝AC ，O 是BC中点，⊙ O 与AB 相切于E.求证：AC 是⊙ O 的切线． B O C E A 分析：根据切线的判定定理， 要证明AC是⊙ O的切线，只要 证明由点O向AC所作的垂线段 OF是⊙ O的半径就可以了，而 OE是⊙ O的半径，因此只需要 证明OF=OE. F 例2 证明：连接OE ，OA, 过O 作OF ⊥AC. ∵⊙ O 与AB 相切于E ， ∴OE ⊥ AB. 又∵△ABC 中，AB ＝AC ， 　　O 是BC 中点． ∴AO 平分∠BAC， F B O C E A ∴OE ＝OF. ∵OE 是⊙ O 半径，OF ＝ OE，OF ⊥ AC. ∴AC 是⊙ O 的切线． 又OE ⊥AB ，OF⊥AC. 如图，已知直线AB经过⊙ O上的 点C，并且OA＝OB，CA＝CB 求证：直线AB是⊙ O的切线. C BA O 如图，OA＝OB=5，AB＝8, ⊙ O的直径为6. 求证：直线AB是⊙ O的切线. C BA O 对比思考 作垂直连接 思考：如图，如果直线l是⊙ O 的切线，点A为切点，那么 OA与l垂直吗？ A l O ∵直线l是⊙ O 的切线，A是切点， ∴直线l ⊥OA. 切线的性质定理 ★切线性质 圆的切线垂直于经过切点的半径． ★应用格式 2 小亮的理由是:直径AB与直线CD要么垂直,要么不垂直. （1）假设AB与CD不垂直,过点O作一条直 径垂直于CD,垂足为M, （2）则OM

查看更多