- 2021-11-11 发布 |
- 37.5 KB |
- 7页


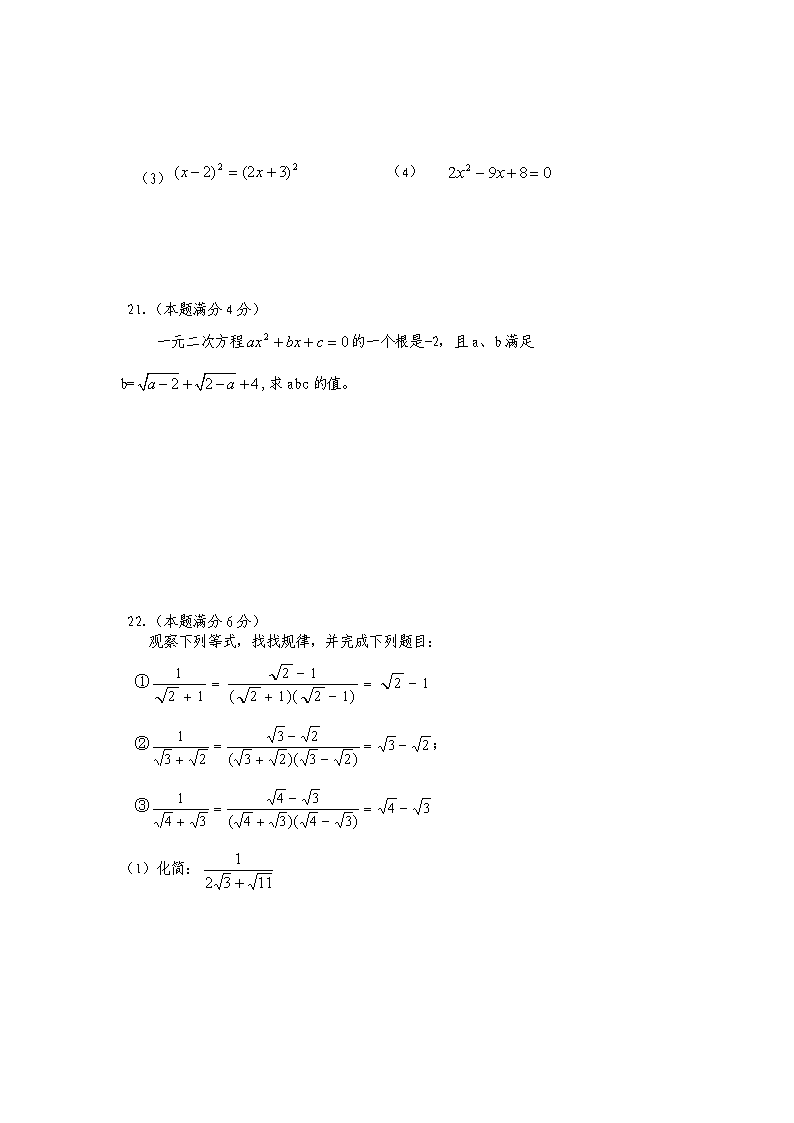
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年江苏省无锡市九年级10月份月考数学试卷
苏教版九年级数学上册 10 月份月考测试卷 一、选择题(本大题共 10 小题,每小题 3 分,共 30 分.在每小题所给出的四个选项中, 只有一项是正确的) 1.式子 2- 1 x x 的取值范围是 ( ) A. x≠ 2 B.x>1 且 x≠ 2 C. x≥1 且 x ≠2 D.x≥1 2.在 27 、 1 12 、 11 2 中与 3 是同类二次根式的个数是( ) A. 0 B.1 C.2 D.3 3.一位运动员在出征奥运会前刻苦进行 110 米跨栏训练,教练对他 10 次的训练成绩进 行分析,判断他的成绩是否稳定,则教练最需要知道运动员 10 次成绩的( ) A.众数 B.平均数 C.方差 D.频数 4.已知⊿ABC 的三边分别为 2、x、5,则化简 22 73 xx 的值为 ( ) A. 2x-10 B.4 C.10-2x D.-4 5. 三角形的两边分别为 2 和 6,第三边是方程 x2-10x+21=0 的解,则第三边的长为 ( ). A.7 B.3 C.7 或 3 D.无法确定 6、一个两位数,个位数字比十位数字大 3,个位数字的平方刚好等于这个两位数,则这 个两位数为( ) A.25 B.36 C.25 或 36 D.16 或 25 7、如果关于 x 的方程 01)12(22 xmxm 有实数根,则 m 的取值范围为( ) A. 4 1m B. 4 1m C. 04 1 mm 且 D. 04 1 mm 且 8、若最简二次根式 2 4 3 10x x x 与 是同类二次根式,则 x 的值是( ) A. 5 或-2 B.-5 或 2 C. 5 D.-2 9、定义:如果一元二次方程 ax2+bx+c=0(a≠0)满足 a+b+c=0,那么我们称这个方程为 “凤凰”方程.已知是“凤凰”方程 ax2+bx+c=0(a≠0),且有两个相等的实数根,则下 列结论正确的是( ) A. a b B. a c C.b c D. a b c 10、菱形 ABCD 的边长是 5,两条对角线交于点 O,且 AO,BO 的长分别是关于 x 的方程 2 2(2 1) 3 0x m x m 的根,则 m 的值为 ( ) A.一 3 B.5 C.5 或一 3 D.一 5 或 3 二、填空题(本大题共 8 小题,每小题 2 分,共 16 分) 11、在实数范围内分解因式 94x . 12.已知样本数据 1,3,x,5 的平均数是 2,则这个样本的方差是 . 13、已知一元二次方程 0331m 22 mmxx 有一个根是 1,则 m 的值 为 . 14.如图,将一根 25cm 长的细木棒放入长、宽、高分别为 8cm、6cm 和 10 3 cm 的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 cm. 15.在实数范围内定义一种运算“﹡”,其规则为 a﹡b=a2-b2,根据这个规则, 方程 (x+1) ﹡3=0 的解为 16.已知 x2+3x+3 的值为 9,则代数式 3x2+9x+12 的值为 17、某厂一月份生产某机器 100 台,计划二、三月份共生产 280 台。设二、三月份每月 的平均增长率为 x,根据题意列出的方程是 。 18、已知(x2+y2+1) (x2+y2-3)=5,则 x2+y2= . 三、解答题(本大题共 10 小题,共 84 分.解答时应写出文字说明、证明过程或演算步 骤) 19.(本题满分 12 分)计算: (1) 104 3-535 44 (2) 22 )3352()3352( (3) (2 12 -3 1 3 )× 6 (4) b ababaa 2 2 24532 ( 0,0 ba ) 20.(本题满分 12 分)解方程: (1) 22 1 0x x . (2) xx 36)2( 2 (3) 22 )32()2( xx (4) 0892 2 xx 21.(本题满分 4 分) 一元二次方程 02 cbxax 的一个根是-2,且 a、b 满足 b= 2 2 4a a , 求 abc 的值。 22.(本题满分 6 分) 观察下列等式,找找规律,并完成下列题目: ① 12 )12)(12( 12 12 1 ② 23 )23)(23( 23 23 1 ; ③ 34 )34)(34( 34 34 1 (1)化简: 1132 1 (2)计算: 1 1 1 1...... 1 2 2 3 3 4 9 10 23.(本题满分 6 分) 如图,D 是△ABC 中 BC 边的中点,E、F 分别在 AD 及其延长线上, CE∥BF,连接 BE、CF. (1)求证:△BDF≌△CDE; (2)若 AB=AC,求证:四边形 BFCE 是菱形. 24.(本题满分 8 分) 为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,我 国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的 爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练 中,所测成绩如图所示,请根据图中所示解答以下问题. (1)请根据图中信息,补齐下面的表格; (2)从图中看,小明与小亮分别是哪次成绩最好? (3)分别计算他们的平均数、极差和方差,若你是他们的教练,将小明与小亮的成绩 比较后,你将分别给予他们怎样的建议? 25.(本题满分 9 分) 已知关于 x 的方程 014)3(2 22 kkxkx . (1)若这个方程有实数根,求 k 的取值范围;(2)若这个方程有一个根为 1,求 k 的值; (3)若以方程 014)3(2 22 kkxkx 的两个根为横坐标、纵坐标的点恰在反比例 函数 x my 的图象上,求满足条件的 m 的最小值. 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 小明 13.3 13.4 13.3 13.3 小亮 13.2 13.1 13.5 13.3 时间(秒) 第1次 第2次 第3次 第4次 第5次 13.6 13.5 13.4 13.3 13.2 13.1 小明 小亮 26.(本题满分 8 分) 某省为解决农村饮用水问题,省财政部门共投资 20 亿元对各市的农村饮用水 的“改水工程”予以一定比例的补助,2008 年,A 市在省财政补助的基础上投入 600 万元用于“改水工程”,计划以后每年以相同的增长率投资,2010 年该市计划投资 “改水工程”1176 万元。 (1)求 A 市投资“改水工程”的年平均增长率; (2)从 2008 年到 2010 年,A 市三年共投资“改水工程”多少万元? 27.(本题满分 9 分) 恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本 和韩国等地.上市时,外商李经理按市场价格 10 元/千克在我州收购了 2000 千克香菇 存放入冷库中.据预测,香菇的市场价格每天每千克将上涨 0.5 元,但冷库存放这批香 菇时每天需要支出各种费用合计 340 元,而且香菇在冷库中最多保存 110 天,同时,平 均每天有 6 千克的香菇损坏不能出售. (1)若存放 x 天后,将这批香菇一次性出售,设这批香菇的销售总金额为 y 元,试写 出 y 与 x 之间的函数关系式. (2)李经理想获得利润 22500 元,需将这批香菇存放多少天后出售?(利润=销售总 金额-收购成本-各种费用) (3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少? 28.(本题满分 10 分)市天一实验学校金杨建录制 QQ:623300747.转载请注明! 如图,已知正方形 ABCD 的边长为 40cm,E 为 AD 边的中点,G 为 BC 的延长线上一点, 连结 EG 交 CD 于点 F. (1)若 FE=FC,求 FC 的长; (2)在(1)的条件下,现有一动点 P,从 A 点出发,以 5cm/s 的速度沿 A→E→F→C 的路线运动,过点 P 作 PM⊥AB 于 M,PN⊥BC 于 N. ①当 t 为何值时,矩形 PMBN 恰好是一个正方形? ②若设矩形 PMBN 的面积为 S,试求 S 与 t 之间的函数关系式,并写出自变量 t 的取 值范围; ③在点 P 从 A 点运动到 C 点的整个过程中,试问是否存在这样的 t 的值,使得矩形 PMBN 的面积恰为 888?若存在,求出 t 的值;若不存在,请说明理由.查看更多