安徽合肥市瑶海区2020-2021学年第一学期八年级期末数学试卷（含答案）

安徽合肥市瑶海区2020-2021学年第一学期八年级期末数学试卷（含答案）

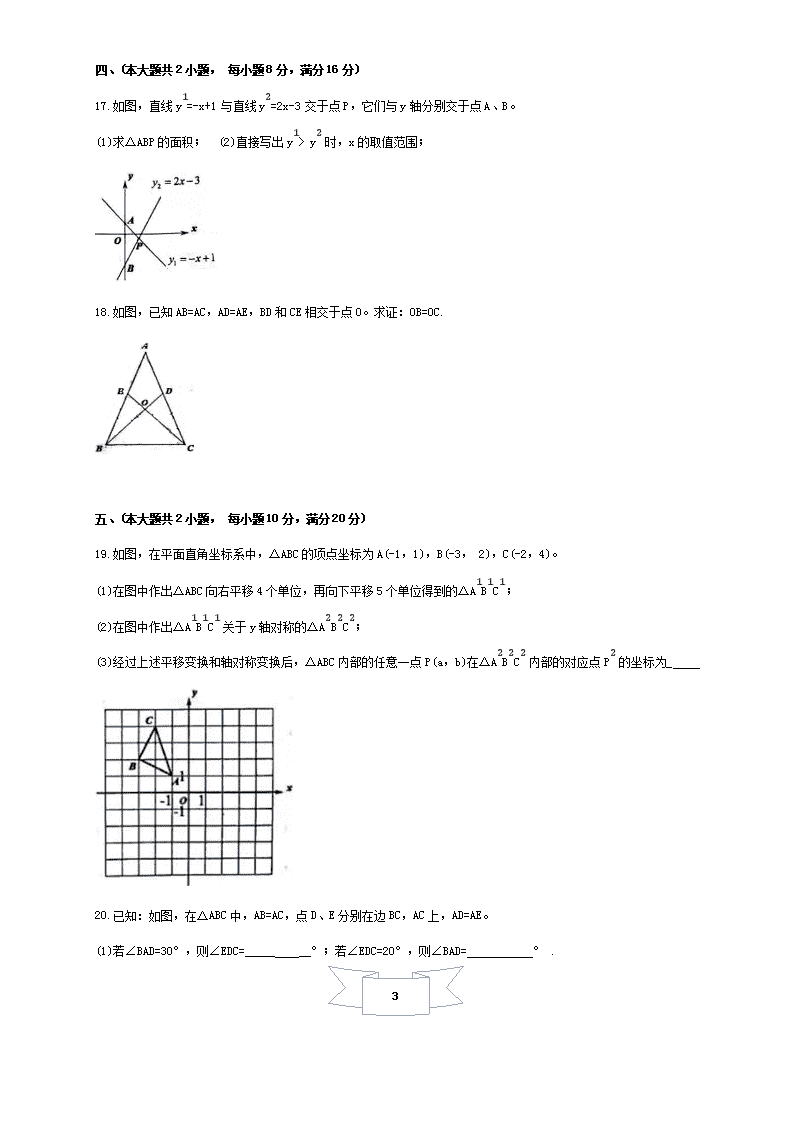
1 合肥瑶海区 2020-2021 第一学期八年级期末数学试卷（含答案） 一、选择题(本大题共 10 小题，每小题 4分，满分 40 分) 1.在平面直角坐标系中，点 P(-1，4)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识，下面是科学防控知识的图片，图片 上有图案和文字说明，其中的图案是轴对称图形的是( ) A 勤洗手 勤通风 B 打喷嚏 捂口鼻 C 喷嚏后 慎揉眼 D 戴口罩 讲卫生 3.若三条线段中 a=3，b=5，c 为奇数，那么以 a、b、c为边组成的三角形共有( ) A.1 个 B.2 个 C.3 个 D.4 个 4.在平面直角坐标系中。已知函数 y=ax+a(a≠0) 的图象过点 P(2，1)，则该函数的图象可能是（ ） A B C D 5.已知等腰三角形的两内角度数之比为 1：4，则这个等腰三角形的项角度数为( ) A. 20° B.120° C. 20 或 120° D. 36° 6.已知点（-4，y1）、（2，y2）都在直线 y=- 1 2 x+b 上，则 y1 和 y2 的大小关系是( ) A. y1> y2 B. y1=y2 C. y1< y2 D.无法确定 7.如图，己知 AE 是△ABC 的角平分线，AD是 BC 边上的高，若∠ABC=34°，∠ACB=64°，则∠DAE 的度数是( ) A.5° B.13° C.15° D.20° 第 7题 第 8题 第 9题 8.如图，已知直线 y=kx+b 和 y=mx+n 交于点 A( -2，3)，与 x 轴分别交于点 B(-1，0)、C(3，0)，则方程组 kx y b mx y n        的解为( ) A 2 3 x y     B 1 0 x y     C 3 0 x y    D 无法确定 9.如图，△ABC 中，∠ABC=45°，CD⊥AB 于 D，BE 平分∠ABC，且 BE⊥AC 于 E，与 CD 相交于点 F， DH⊥BC 于 H， 交 BE于 G下列结论：①△BCD 为等腰三角形；②BF=AC；③CE= 1 2 BF；④BH=CE。其中正确的序号是( ) A.①② B.①③ C.①②③ D.①②③④ 10.如图，已知在△ABC 中，AB=AC，点 D 沿 BC 自 B 向 C 运动，作 BE⊥AD 于 E，CF⊥AD 于 F，则 BE+CF 的值 y 与 BD 的长 x之间的函数图象大致是( ) A B C D 2 二、填空题(本大题共 4小题，每小题 5分，满分 20 分) 11.函数 y= 2 1x  中自变量 x的取值范围是_ 12.命题“全等三角形的周长相等”的逆命题是__ 命题(填“真”或“假”) 13.已知：如图，△ABC 中，∠ACB=90°，CD是斜边上的高，∠A=30°，BD=2，则 AD= 14.在平面直角坐标系中，A(2，2)、B(3，-3)，若一次函数 y=kx-1 与线段 AB 有且只有一个交点，则 k 的取值范围 是_ 三、(本大题共 2小题， 每小题 8分，满分 16 分) 15.△ABC 中，∠A= 1 3 ∠B= 1 5 ∠C，通过计算，判断△ABC 的形状。 16.已知：如图，△ABC 中，∠ABC 的平分线 BD与∠ACB 的平分线 CE 交于点 I，连接 AI 并延长交 BC于点 F。 求证：AF 平分∠BAC 四、(本大题共 2小题， 每小题 8分，满分 16 分) 17.如图，直线 y1=-x+1 与直线 y2=2x-3 交于点 P，它们与 y轴分别交于点 A、B。 (1)求△ABP 的面积； (2)直接写出 y1> y2 时，x 的取值范围； 18.如图，已知 AB=AC，AD=AE，BD 和 CE相交于点 0。求证：OB=OC. 3 五、(本大题共 2小题， 每小题 10 分，满分 20 分) 19.如图，在平面直角坐标系中，△ABC 的项点坐标为 A(-1，1)，B(-3， 2)，C(-2，4)。 (1)在图中作出△ABC 向右平移 4 个单位，再向下平移 5 个单位得到的△A1B1C1； (2)在图中作出△A1B1C1 关于 y轴对称的△A2B2C2； (3)经过上述平移变换和轴对称变换后，△ABC 内部的任意一点 P(a，b)在△A2B2C2 内部的对应点 P2 的坐标为_ 20.已知：如图，在△ABC 中，AB=AC，点 D、E 分别在边 BC，AC 上，AD=AE。 (1)若∠BAD=30°，则∠EDC=_____ __°；若∠EDC=20°，则∠BAD= ° . (2)设∠BAD=x，∠EDC=y，写出 y与 x之间的关系式，并给出证明。 六、(本大题满分 12 分) 21、某商店销售 10台 A型和 20 台 B型电脑的利润为 6400 元,销售 20台 A型和 10 台 B型电脑的利润为 5600 元。 (1)求每台 A型电脑和 B型电脑的销售利润； (2)该商店计划一次购进两种型号的电脑共 100 台，其中 B型电脑的进货量不超过 A型电脑的 2倍.设购进 A 型电脑 x 台，这 100 台电脑的销售总利润为 y元。 ①求 y关于 x的函数关系式； ②该商店购进 A型、B型电脑各多少台，才能使销售总利润最大，最大销售总利润是多少元? 4 七、(本大题满分 12 分) 22.如图，在△ABC 中，AB=AC，AF⊥BC，在△CDE 中，DC=DE，DG⊥CE，AF 和 DG 的延长线交于点 P，连接 BP、EP。 (1)求证：BP=EP； (2)若∠BCE=135°，试判断△PBE 的形状，并给出证明. 八、(本大题满分 14 分) 23.已知： (1)0 是∠BAC 内部的一点。 ①如图 1，求证：∠BOC> ∠A； ②如图 2，若 OA=OB=OC，试探究∠BOC 与∠BAC 的数量关系，给出证明； (2)如图 3，当点 0 在∠BAC 的外部，且 0A=OB=OC，继续探究∠BOC 与∠BAC 的数量关系，给出证明。 5 合肥瑶海区 2020-2021 第一学期八年级期末数学试卷答案 1 2 3 4 5 6 7 8 9 10 B D C C C A C A C D 11、 x≠1； 12、 假； 13、 6； 14、 - 2 3 ≤x≤ 3 2 15、设∠A=x，则∠B=3x，∠C=5x，即 x+3x+5x=180°，x=20°，∴∠A=20°，∠B=60°，∠C=100°， 所以△ABC 的形状为钝角三角形； 16、如图所示，∵BD 平分∠ABC，CE 平分∠ACB，过点 I分别作 IG⊥BC、IH⊥AC、IK⊥AB， 垂足分别 G、H、K，则：IG=IH，IG=IK，∴IH=IK，∴AF平分∠BAC 17、（1） 8 3 ； （2）x＜ 4 3 18、证明：∵AB=AC，AD=AE，∠A=∠A，∴△AEC≌△ADB，∴∠ACE=∠ABD， ∵AB=AC，∴∠ABC=∠ACB，∴∠OBC=∠OCB，∴OB=OC 19、（1）如图所示： （2）如图所示； （3）P（-a-4，b-5）； 20、（1）15°；40°； （2）y 与 x 之间的关系式为 y= 1 2 x； 证明：∵AB=AC，∴∠B=∠C，∵AD=AE，∴∠ADE=∠AED=y+∠C，∴∠ADC=∠ADE+∠EDC=2y+∠C=∠B+x； 即 2y=x，∴y= 1 2 x 21、（1）160 元，240 元； （2）①y=-80x+24000； ②A 型 34 台，B型 66 台时，最大利润为 21280 元。 22、（1）∵AB=AC，AF⊥BC， DC=DE，DG⊥CE，∴AP、DP 分别为线段 BC、CE 的垂直平分线，连接 PC， 则 PC=PB，PC=PE，∴PB=PE。 （2）△PBE 的形状为等腰直角三角形； 6 证明：∵∠BCE=135°，∠PGC=∠PFC=90°，在 Rt△PGC 和 Rt△PFC 中，∠FPC+∠GPC=45°； ∵AP、DP 分别为线段 BC、CE 的垂直平分线，∠FPC=∠FPB，∠GPC=∠GPE，∴∠BPE=2（∠FPC+∠GPC）=90°； ∵PB=PE，∴△PBE 的形状为等腰直角三角形； 23、（1）①如图所示：①连接 AO 并延长 AO至点 E，则∠BOE＞∠BAO，∠COE＞∠CAO，∴∠BOC> ∠A； ②∠BOC 与∠BAC 的数量关系：∠BOC=2∠A； 证明：如图所示，延长 AO至点 E，则∠BOE=∠BAO+∠B，∠COE=∠CAO+∠C，∵0A=OB=OC， ∴∠BAO=∠B，∠CAO=∠C，∴∠BOC=∠COE+，∠COE=∠BAO+∠B+∠CAO+∠C=2（∠BAO+∠CAO）=2∠BAC=2∠A； （2）∠BOC 与∠BAC 的数量关系：∠BOC=2∠BAC； 证明：如图所示，设∠B=x，∵0A=OB=OC，∴∠B=∠BAO=x，∠C=∠OAC=∠BAC+x； 在△BEO 和△AEC 中，有：∠B+∠BOC=∠C+∠CAE；即 x+∠BOC=∠CAE+x+∠CAE=2∠BAC+x；即∠BOC=2∠BAC；