探索三角形相似的条件学案(2)

探索三角形相似的条件学案(2)

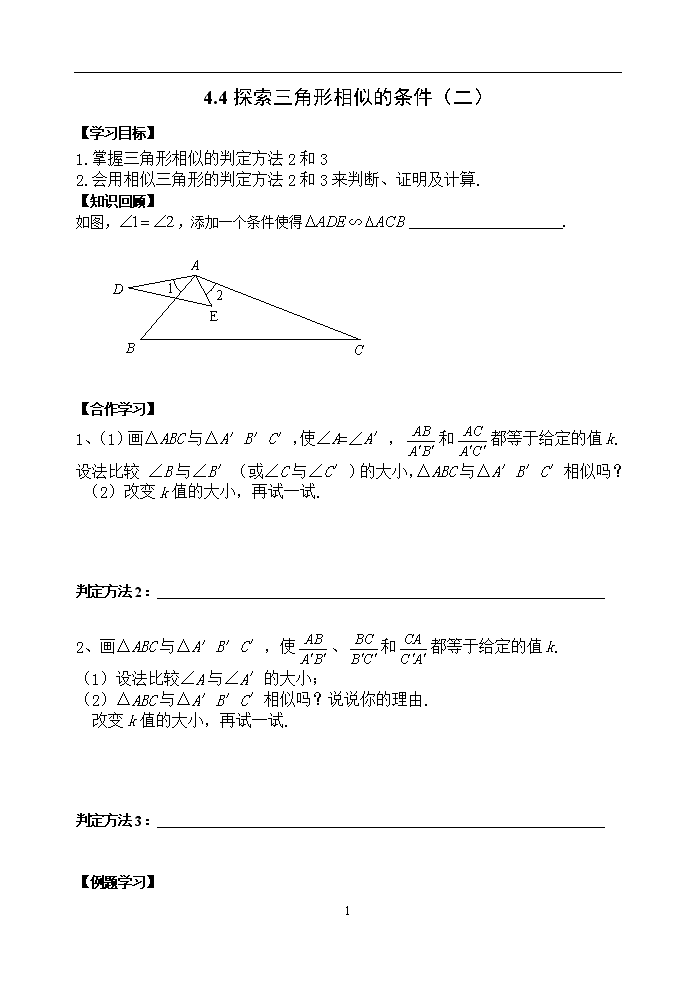
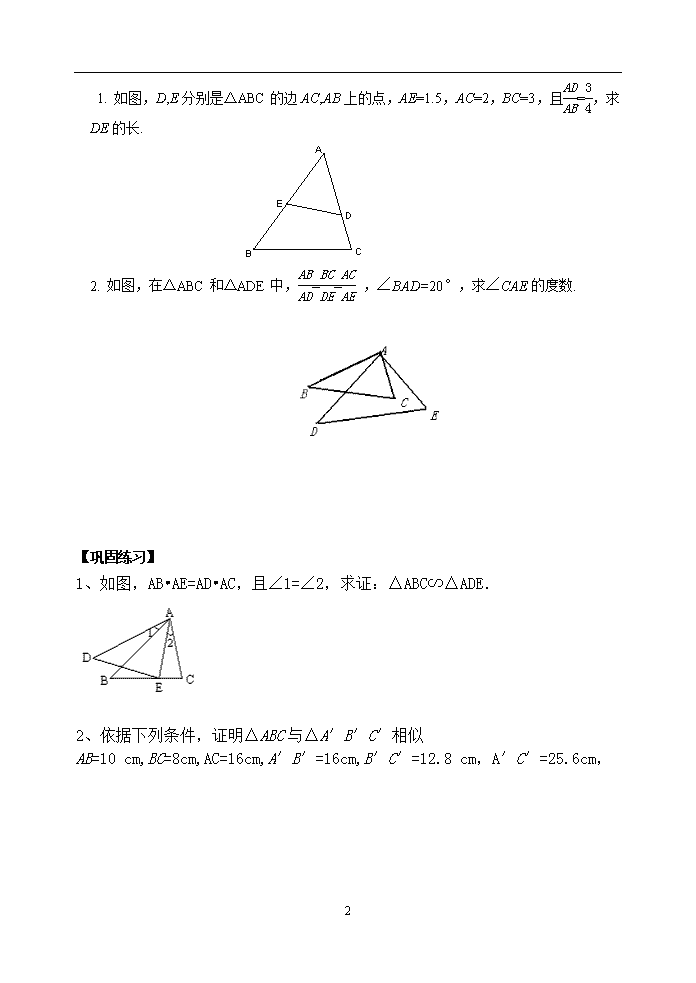
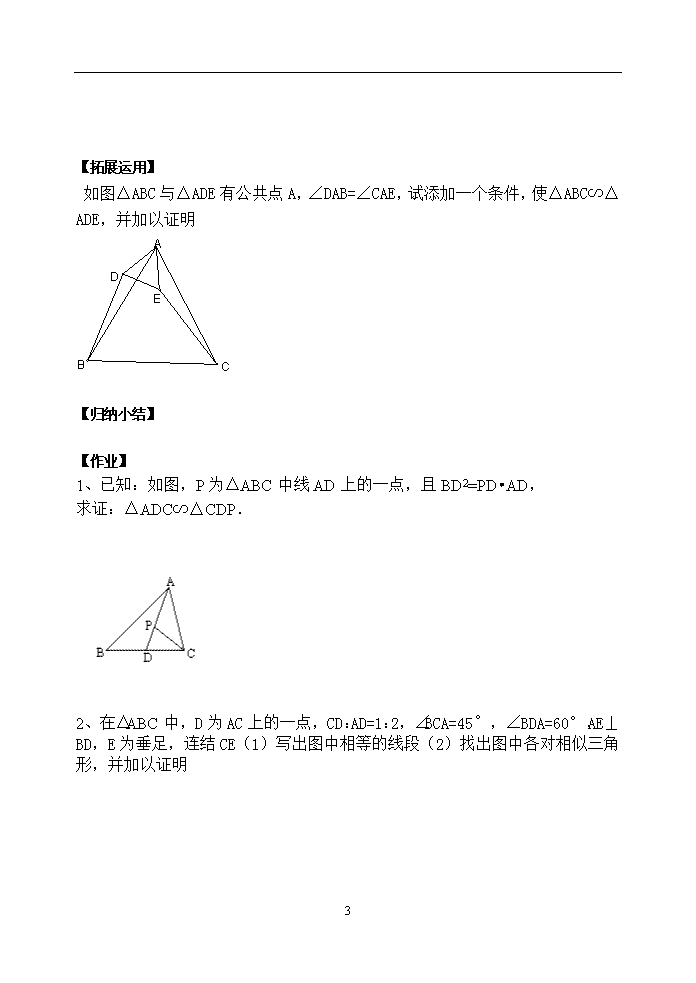
‎4.4探索三角形相似的条件（二）‎ ‎【学习目标】‎ ‎1.掌握三角形相似的判定方法2和3‎ ‎2.会用相似三角形的判定方法2和3来判断、证明及计算.‎ ‎【知识回顾】‎ 如图，，添加一个条件使得∽ .‎ ‎【合作学习】‎ ‎1、（1）画△ABC与△A′B′C′，使∠A=∠A′，和都等于给定的值k.设法比较 ∠B与∠B′（或∠C与∠C′）的大小，△ABC与△A′B′C′相似吗？‎ ‎（2）改变k值的大小，再试一试.‎ 判定方法2： ‎ ‎2、画△ABC与△A′B′C′，使、和都等于给定的值k.‎ ‎（1）设法比较∠A与∠A′的大小；‎ ‎（2）△ABC与△A′B′C′相似吗？说说你的理由.‎ 改变k值的大小，再试一试.‎ 判定方法3： ‎ ‎【例题学习】‎ 4‎ ‎1. 如图，D,E分别是△ABC的边AC,AB上的点，AE=1.5，AC=2，BC=3，且=，求DE的长.‎ ‎ ‎ ‎2. 如图，在△ABC和△ADE中，== ，∠BAD=20°，求∠CAE的度数.‎ ‎【巩固练习】‎ ‎1、如图，AB•AE=AD•AC，且∠1=∠2，求证：△ABC∽△ADE．‎ ‎2、依据下列条件，证明△ABC与△A′B′C′相似 AB=10 cm,BC=8cm,AC=16cm,A′B′=16cm,B′C′=12.8 cm，A′C′=25.6cm， ‎ 4‎ ‎【拓展运用】‎ 如图△ABC与△ADE有公共点A，∠DAB=∠CAE，试添加一个条件，使△ABC∽△ADE，并加以证明 ‎【归纳小结】‎ ‎【作业】‎ ‎1、已知：如图，P为△ABC中线AD上的一点，且BD2=PD•AD，‎ 求证：△ADC∽△CDP．‎ ‎2、在△ABC中，D为AC上的一点，CD：AD=1：2，∠BCA=45°，∠BDA=60°，AE⊥BD，E为垂足，连结CE（1）写出图中相等的线段（2）找出图中各对相似三角形，并加以证明 4‎ ‎【教学反思】‎ 4‎