配方法第1课时教案

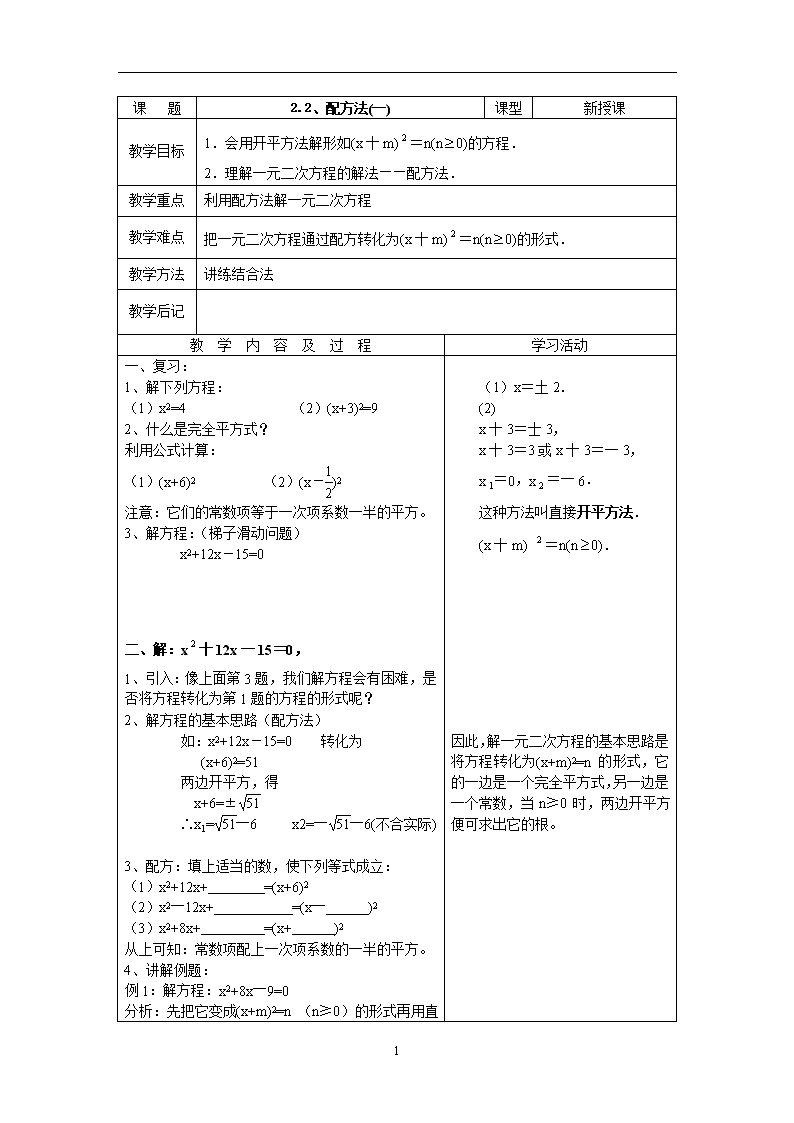
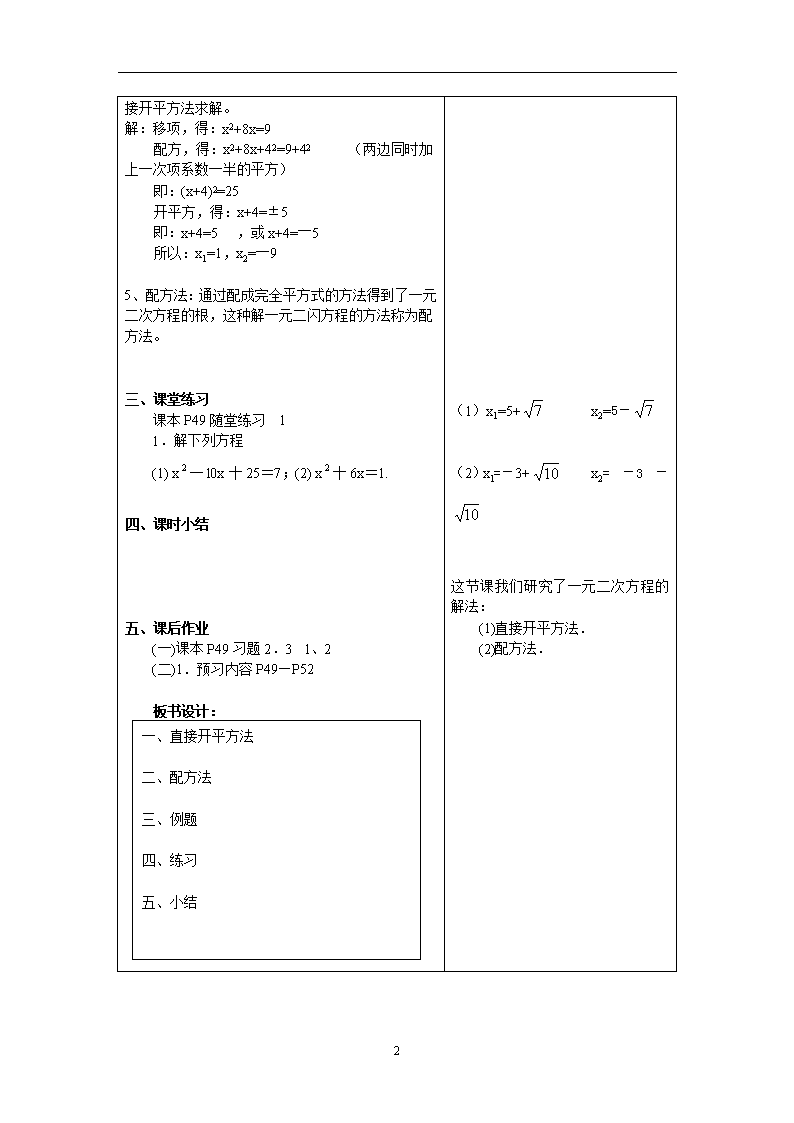
配方法第1课时教案

课 题 ‎2.2、配方法(一)‎ 课型 新授课 教学目标 ‎1．会用开平方法解形如(x十m)＝n(n0)的方程．‎ ‎2．理解一元二次方程的解法——配方法．‎ 教学重点 利用配方法解一元二次方程 教学难点 把一元二次方程通过配方转化为(x十m)＝n(n0)的形式．‎ 教学方法 讲练结合法 教学后记 教 学 内 容 及 过 程 学习活动 一、复习：‎ ‎1、解下列方程：‎ ‎（1）x2=4 （2）(x+3)2=9‎ ‎2、什么是完全平方式？‎ 利用公式计算：‎ ‎（1）(x+6)2 （2）(x－)2‎ 注意：它们的常数项等于一次项系数一半的平方。‎ ‎3、解方程：（梯子滑动问题）‎ x2+12x－15=0‎ 二、解：x十12x一15＝0，‎ ‎1、引入：像上面第3题，我们解方程会有困难，是否将方程转化为第1题的方程的形式呢？‎ ‎2、解方程的基本思路（配方法）‎ 如：x2+12x－15=0 转化为 ‎ (x+6)2=51‎ 两边开平方，得 ‎ x+6=± ‎∴x1=―6 x2=――6(不合实际)‎ ‎3、配方：填上适当的数，使下列等式成立：‎ ‎（1）x2+12x+ =(x+6)2‎ ‎（2）x2―12x+ =(x― )2‎ ‎（3）x2+8x+ =(x+ )2‎ 从上可知：常数项配上一次项系数的一半的平方。‎ ‎4、讲解例题：‎ 例1：解方程：x2+8x―9=0‎ 分析：先把它变成(x+m)2=n （n≥‎ ‎（1）x＝土2．‎ ‎(2)‎ x十3＝士3，‎ x十3＝3或x十3＝一3，‎ x＝0，x＝一6．‎ 这种方法叫直接开平方法．‎ ‎(x十m) ＝n(n0)．‎ 因此，解一元二次方程的基本思路是将方程转化为(x+m)2=n 的形式，它的一边是一个完全平方式，另一边是一个常数，当n≥0 时，两边开平方便可求出它的根。‎ 2‎ ‎0）的形式再用直接开平方法求解。‎ 解：移项，得：x2+8x=9‎ 配方，得：x2+8x+42=9+42 （两边同时加上一次项系数一半的平方）‎ 即：(x+4)2=25‎ 开平方，得：x+4=±5‎ 即：x+4=5 ，或x+4=―5‎ 所以：x1=1，x2=―9‎ ‎5、配方法：通过配成完全平方式的方法得到了一元二次方程的根，这种解一元二闪方程的方法称为配方法。‎ 三、课堂练习 课本P49随堂练习 1‎ ‎1．解下列方程 ‎(1) x一l0x十25＝7；(2) x十6x＝1.‎ 四、课时小结 五、课后作业 ‎(一)课本P49习题2．3 l、2‎ ‎ (二)1．预习内容P49—P52‎ 板书设计：‎ 一、 直接开平方法 二、 配方法 三、 例题 四、 练习 五、 小结 ‎（1）x1=5+ x2=5－‎ ‎（2）x1=－3+ x2=－3－‎ 这节课我们研究了一元二次方程的解法：‎ ‎ (1)直接开平方法．‎ ‎ (2)配方法．‎ 2‎