平行线分线段成例学案

平行线分线段成例学案

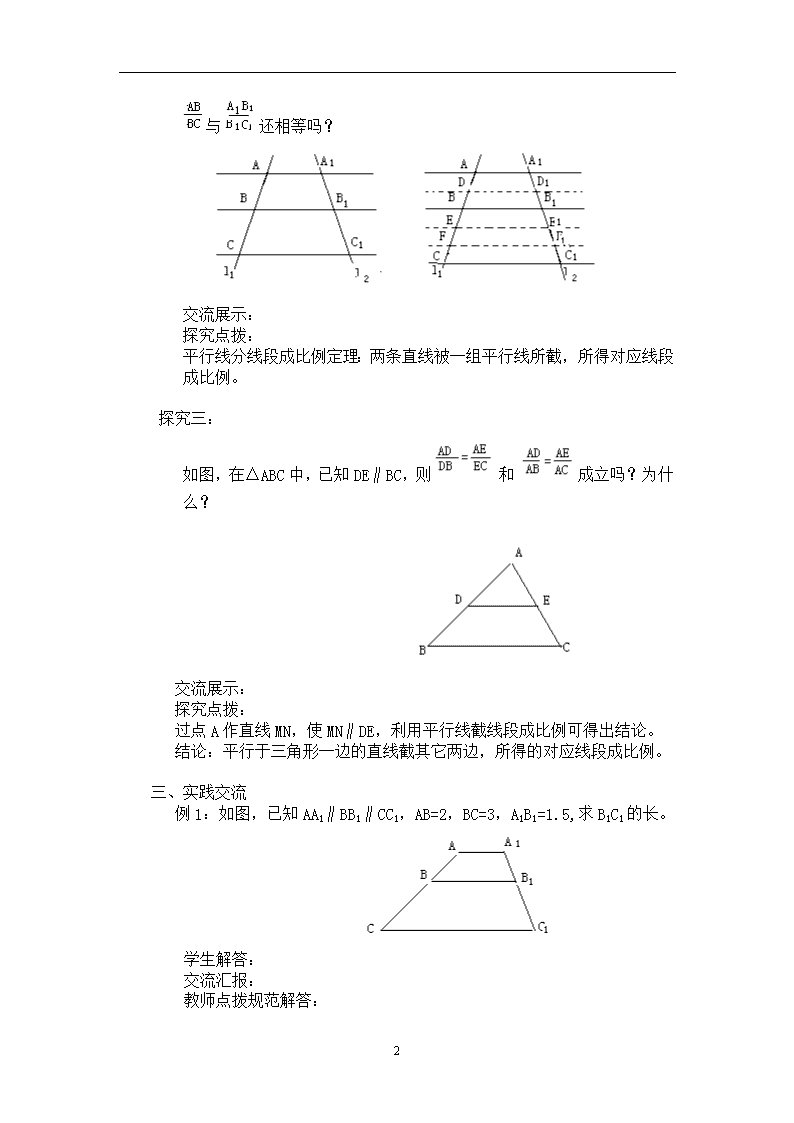
平行线分线段成比例 学习目标：‎ ‎1、理解平行线分线段成比例定理 ‎2、灵活运用定理解答题目 学习重点：平行线等分线段成比例定理及其应用 学习难点：平行线等分线段成比例的推导 学习过程：‎ 一、问题引入 ‎1、比例的基本性质是什么？还有其它什么性质？‎ ‎2、什么叫成比例线段？‎ 二、问题探究 探究一：‎ 如图是一架梯子的示意图，由生活常识可以知道：AA1，BB1，CC1，DD1，‎ 互相平行，且若AB=BC，则A1B1=B1C1，由此可以猜测：若两条直线被一组平行线所截，如果在其中一条直线上截得的线段相等，那么在另一条直线上截得的线段也相等吗？‎ 交流展示：‎ 探究点拨：‎ 设直线a∥b∥c,直线l1,l2被直线a,b,c截得的线段分别为AB，BC和Ａ１Ｂ１，Ｂ１Ｃ１，且ＡＢ＝ＢＣ。过点Ｂ作直线l3∥l2,分别交直线a,c于点A2，C2，由于a∥b∥c，l3∥l2，因此由“夹在两平行线之间的平行线段相等”可知A2B=A1B1，BC2=B1C1，再证明△BAA2≌△BCC2，从而得到A1B1=B1C1.‎ 归纳总结：‎ 平行线等分线段定理：两条直线被一组平行线所截，如果在其中一条直线上截得的线段相还等，那么在另一条直线上截得的线段也相等。‎ 探究二：‎ 任意画两条直线l1,l2，再画三条与l1,l2相交的平行直线a,b,c，分别度量l1,l2被直线a,b,c截得的线段AB，BC，A1B1，B1C1的长度，‎ 相等吗？任意平移直线 c ,再度量AB，BC，A1B1，B1C1的长度，‎ 4‎ 与还相等吗？‎ 交流展示：‎ 探究点拨：‎ 平行线分线段成比例定理：两条直线被一组平行线所截，所得对应线段成比例。‎ 探究三：‎ 如图，在△ABC中，已知DE∥BC，则和成立吗？为什么？‎ 交流展示：‎ 探究点拨：‎ 过点A作直线MN，使MN∥DE，利用平行线截线段成比例可得出结论。‎ 结论：平行于三角形一边的直线截其它两边，所得的对应线段成比例。‎ 三、实践交流 例1：如图，已知AA1∥BB1∥CC1，AB=2，BC=3，A1B1=1.5,求B1C1的长。‎ ‎ ‎ ‎ 学生解答：‎ ‎ 交流汇报：‎ ‎ 教师点拨规范解答：‎ 4‎ ‎ 思路点拨：由平行线分线段成比例可知：=，再将已知线段的值代入就可求出B1C1的长。‎ ‎ 例2、如，AD平分∠BAC交BC于点D，求证：‎ 学生解答：‎ 交流汇报：‎ 教师点拨规范解答：‎ 思路点拨：过C点作CE∥AD，交BA的延长线于点E，易得，再证明AE=AC。‎ 四、课堂小结 ‎1、本节课你有什么收获？‎ ‎2、平行线等分线段定理的内容是什么？‎ ‎3、平行线分线段成比例定理的内容是什么？‎ ‎4、平行于三角形一边的直线截其它两边，所得的对应线段有什么关系？‎ 五、达标检测：‎ 必做题：‎ ‎1、在ABCD中，AE交BC的延长线于点E，交DC于点F，若BC：CE=3：2，则CF：FD=＿＿＿＿。‎ ‎2、如图，已知DE∥BC，DF∥AC，下列比例式正确的是（ ）‎ ‎3、如图，EF∥BC，AB∥DC，AE=9，BE=12，FD=10，则BF=＿＿＿＿。‎ ‎4、如图，在△ABC中，DE∥AC，DF∥AE，BD：DA=3：2，BF=6cm,则EF=＿＿＿＿，EC=＿＿＿＿。‎ 4‎ ‎5、在ABCD中，E是AB延长线上一点，且，若BC=6，求BF的长度。‎ 选做题：‎ 如图，在△ABC中，D为BC边的中点，延长AD至E，延长AB交CE的延长线于点P，若AD=2DE，求证：AP=3AB.‎ 4‎