中考数学复习专题十六:解选择题的策略
中考数学复习专题16 解选择题的策略
概述:
1.选择题在中考中占的比例较大,题比较基础,做题时要细心认真,失分很不合算,因为它只要一个答案,并不看你的解答过程,若在某个细节上出问题,全题就一分不得.
2.解选择题的方法大致有以下几种:综合法、分析法、验算法、排除法(筛选法)等.
典型例题精析
例1.在下列计算中,正确的是( )
(A)(ab2)3=ab6 (B)(3xy)3=9x3y3
(C)(-2a2)2=-4a4 (D)(-2)-2=
解:宜用排除法.(A)中,没有3次方,(B)中32≠9,(C)中(-2)2≠4.
∴应选D.
例2.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为( )
(A)6 (B)4 (C)3 (D)1
解:宜用综合法,令x2-4x+3=0,得x1=1,x2=3,
∴│AB│=│3-1│=2,令x=0得y=3.
∴C(0,3),即△CAB中,AB边上的高为3,
∴S△ABC=×2×3=3 故选(C).
例3.若m
0 (B)>1 (C)m-5>n-5 (D)-3m>-3n
解:可用验值法,取m=-10,n=-2进行验算.
(A)n-m=-2-(-10)=-2+8>0正确.
(B)==5>1正确.
(C)-10-5=-15,n-5=-2-5=-7 m-5>n-5错误.
(D)-3m=-3·(-10)=30,-3n=-3×(-2)=5
∴-3m>-3n正确. ∴选(C)
例4.有如下四个结论:
①有两边及一角对应相等的两个三角形全等.
②菱形既是轴对称图形,又是中心对称图形.
③平分弦的直径垂直于弦,并且平分弦所对的两条弦.
④两圆的公切线最多有4条.
其中正确的结论的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
解:宜用筛选法
①两边必须为夹角,因此错.
②平分弦中的弦应指明不为直径,因此错.故选(B).
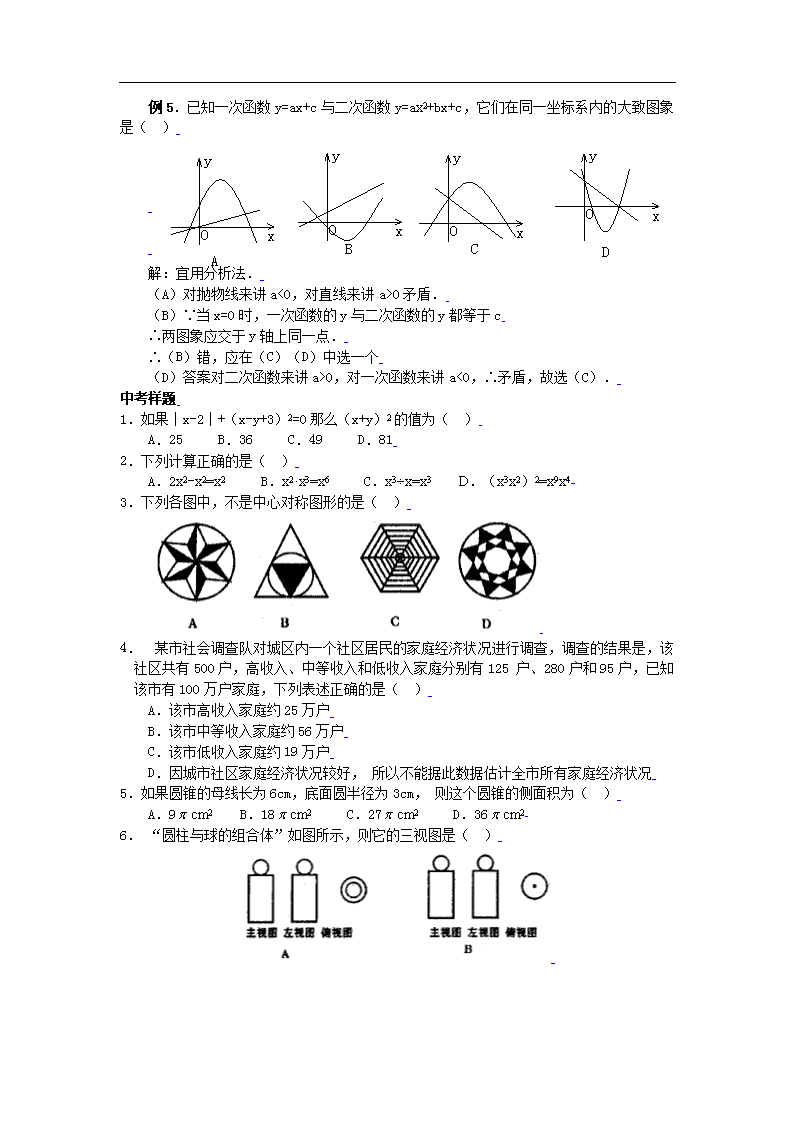
例5.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
解:宜用分析法.
(A)对抛物线来讲a<0,对直线来讲a>0矛盾.
(B)∵当x=0时,一次函数的y与二次函数的y都等于c
∴两图象应交于y轴上同一点.
∴(B)错,应在(C)(D)中选一个
(D)答案对二次函数来讲a>0,对一次函数来讲a<0,∴矛盾,故选(C).
中考样题
1.如果│x-2│+(x-y+3)2=0那么(x+y)2的值为( )
A.25 B.36 C.49 D.81
2.下列计算正确的是( )
A.2x2-x2=x2 B.x2·x3=x6 C.x3÷x=x3 D.(x3x2)2=x9x4
3.下列各图中,不是中心对称图形的是( )
4. 某市社会调查队对城区内一个社区居民的家庭经济状况进行调查,调查的结果是,该社区共有500户,高收入、中等收入和低收入家庭分别有125户、280户和95户,已知该市有100万户家庭,下列表述正确的是( )
A.该市高收入家庭约25万户
B.该市中等收入家庭约56万户
C.该市低收入家庭约19万户
D.因城市社区家庭经济状况较好,所以不能据此数据估计全市所有家庭经济状况
5.如果圆锥的母线长为6cm,底面圆半径为3cm,则这个圆锥的侧面积为( )
A.9cm2 B.18cm2 C.27cm2 D.36cm2
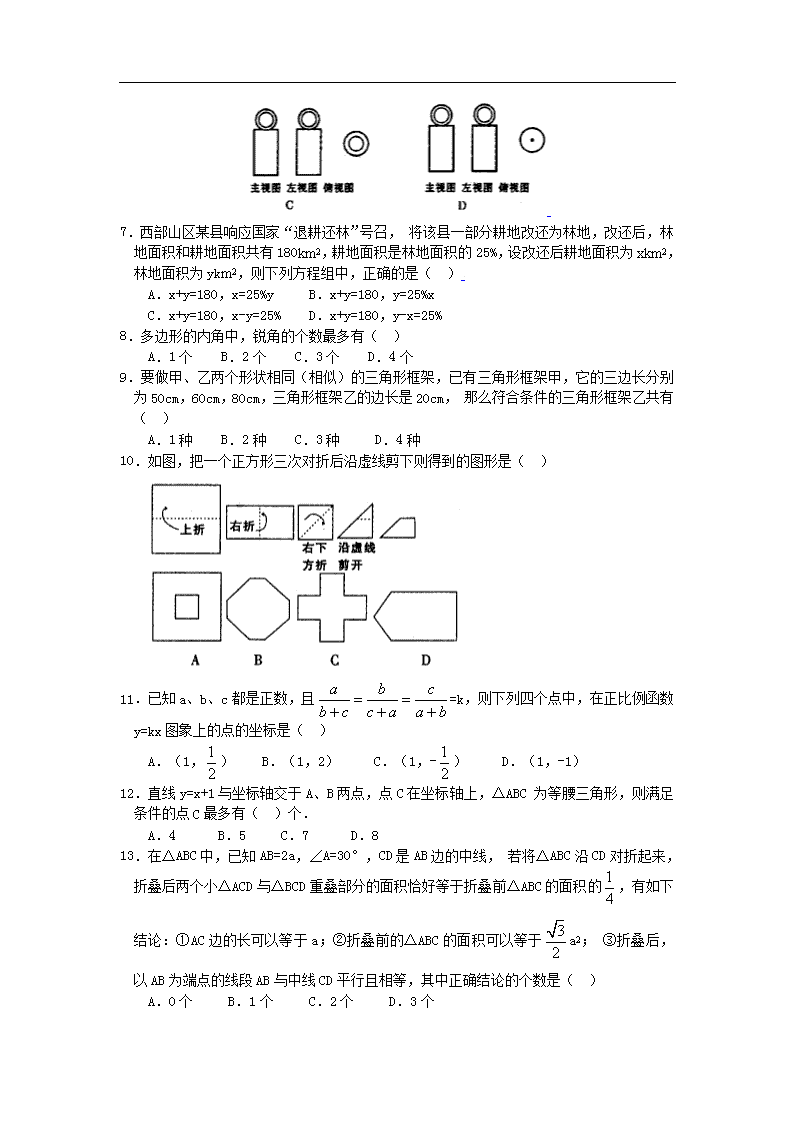
6. “圆柱与球的组合体”如图所示,则它的三视图是( )
7.西部山区某县响应国家“退耕还林”号召,将该县一部分耕地改还为林地,改还后,林地面积和耕地面积共有180km2,耕地面积是林地面积的25%,设改还后耕地面积为xkm2,林地面积为ykm2,则下列方程组中,正确的是( )
A.x+y=180,x=25%y B.x+y=180,y=25%x
C.x+y=180,x-y=25% D.x+y=180,y-x=25%
8.多边形的内角中,锐角的个数最多有( )
A.1个 B.2个 C.3个 D.4个
9.要做甲、乙两个形状相同(相似)的三角形框架,已有三角形框架甲,它的三边长分别为50cm,60cm,80cm,三角形框架乙的边长是20cm,那么符合条件的三角形框架乙共有( )
A.1种 B.2种 C.3种 D.4种
10.如图,把一个正方形三次对折后沿虚线剪下则得到的图形是( )
11.已知a、b、c都是正数,且=k,则下列四个点中,在正比例函数y=kx图象上的点的坐标是( )
A.(1,) B.(1,2) C.(1,-) D.(1,-1)
12.直线y=x+1与坐标轴交于A、B两点,点C在坐标轴上,△ABC为等腰三角形,则满足条件的点C最多有( )个.
A.4 B.5 C.7 D.8
13.在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的,有如下结论:①AC边的长可以等于a;②折叠前的△ABC的面积可以等于a2;③折叠后,以AB为端点的线段AB与中线CD平行且相等,其中正确结论的个数是( )
A.0个 B.1个 C.2个 D.3个
考前热身训练
1.若x<2,化简+│3-x│的正确结果是( )
(A)-1 (B)1 (C)2x-5 (D)5-2x
2.函数y=中自变量x的取值范围是( )
(A)x≤且x≠0 (B)x>-且x≠0
(C)x≠0 (D)x<且x≠0
3.以下命题:
①同一平面内的两条直线不相交就平行;
②三角形的外角必大于其内角;
③两边和其中一边的对角对应相等的两个三角形全等;
④两个全等三角形面积相等.
其中的真命题是( )
(A)①③ (B)①④ (C)①②④ (D)②③④
4.纳米是一种长度单位,1纳米=10-9米,已知某种植物花粉的直径为35000纳米,那么用科学记数法表示该种花粉的直径为( )
(A)3.5×104米 (B)3.5×10-4米 (C)3.5×10-5米 (D)3.5×10-9米
5.下列各式中,正确的是( )
(A)=±4 (B)(3a3)2=6a6
(C)=()-1-()-1=- (D)(-3.14)0=1
6.下列结论:
①方程=-2没有实数根;
②解方程()2-2()=0时,若设=y,则原方程变形为y2-2y-3=0;
③存在这样的两个实数a、b,使得+=;
④当a≠0时,关于x的方程ax=b总有实数根;
其中正确的是( )
(A)①②③ (B)①②④
(C)①③④ (D)②③④
7.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形使所作三角形与△ABC全等,这样的三角形最多可能画出( )
(A)2个 (B)4个 (C)6个 (D)7个
8.点P是△ABC中AB边上的一点,过P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有( )
(A)2条 (B)3条 (C)4条 (D)5条
9.为了让人们感受丢弃塑料袋对环境造成的影响,某班环保小组的6名同学记录了自己家中一周内丢弃的塑料袋数量,结果如下(单位:个)33,25,28,26,25,31,如果该班有45名同学,那么根据提供的数据估计本周全班同学各家总丢弃塑料袋的总量约为( )
(A)900个 (B)1080个 (C)1260个 (D)1800个
10.制造一种产品,原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本( )
(A)8.5% (B)9% (C)9.5% (D)10%
11.相交两圆的公共弦长为16cm,若两圆的半径为10cm和17cm,则两圆的圆心距长为( )
(A)7cm (B)16cm (C)21cm或9cm (D)27cm
12.已知四边形ABCD的对角线AC与BD相交于点O,若S△AOB=4,S△COD=9,则四边形ABCD的面积的最小值为( )
(A)21 (B)25 (C)26 (D)36
答案:
中考样题
1.C 2.A 3.B 4.D 5.B 6.A 7.A 8.C 9.C 10.B 11.A 12.C 13.D
考前热身训练
1.D 2.A 3.B 4.C 5.D 6.C 7.B 8.C 9.C 10.D 11.C 12.B