人教版七年级上册数学第二章 整式加减导学案

人教版七年级上册数学第二章 整式加减导学案

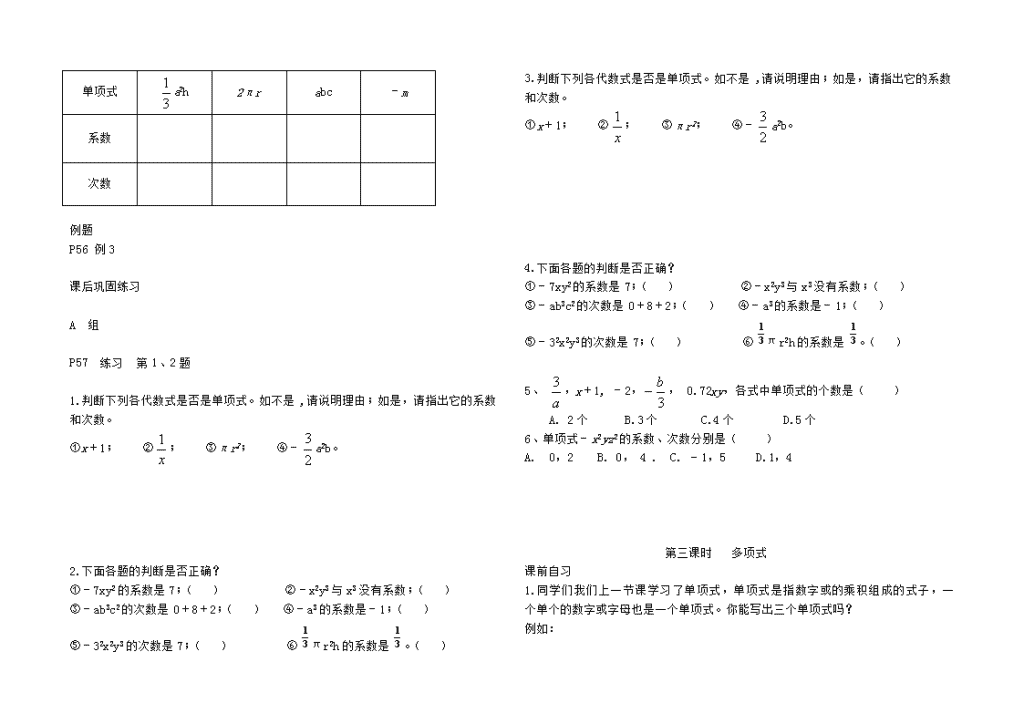
第二章 整式的加减 第一课时 用字母代替数 课前自习 1. 同学们，我们在小学数学中学习了很多数的运算 例如：小明上学的速度是 0.5 千米每分钟，那么小明从家出发 30 分钟后，他离 家千米。 同学们在做这个题目时是怎样做的呢?小明的速度是：0.5 千米每分，也就是说 他 1 分钟走 0.5 千米，那么他 30 分钟走多远呢？可得式子： 0.5 30 (________)  千米 同理： 同学们想一想小明 32 分钟离家又是多远呢？ 同学们想一想小明 33 分钟离家又是多远呢？ 那如果我们不知道是多少时间，我们假设为 X 那又应该是多少千米？ 式子表示为： 这个问题中的 X 是一个未知数，它可代表有意义的任何数，例如：当小明走了 2 分钟时，这时 X=2，小明走了 5 分钟时，X=5，但在这里 X 不能等于负数，因为 时间不能为负。 这就很方便的表示出了所有的时间与小明的路程的关系，像这种用一个字母代 替数的方法，我们就称为“代数”用字母表示的式子我们就称为代数式。 32 32 32b b b    在含有字母和数字的式子中，一般乘号可以省略(数字在字母前面)或写为 例如： 可写为： 或是 例如： (1)若边长为 a 的正方体的表面积为________，体积为； (2)铅笔的单价是 x 元，圆珠笔的单价是铅笔的 2.5 倍 圆珠笔的单价是元； (3) 一辆汽车的速度是 v 千米/小时，行驶 t 小时所走的路程是_______千米； (4) 设 n 是一个数，则它的相反数是________． 2.例题解析 P54 例 1、例 2 练习：P56 练习（1）（2）（3）（4） 课后巩固练习 A 组 P58 习题 2.1 第 1、2 题 B 组 1. 有一个三角形，底长边为 3，高为 m，那这个三角形的面积为： 2. 有一个平行四边形，底边长为 n，这条边上的高为 20，那么它的面积应该为 3.有一个圆，半径为 r，那它的周长应该为：面积为： 4.有一个圆柱，它的底面圆半径为 r，高为 8，那么它的体积为： 5.有一个圆锥，它的底圆半径为 r，高为 7，那么它的体积为： 6.有一个长方形，长为 10，宽为 m，那么它的面积为： 7.有一个正方形，边长为 h，那么它的面积应该是： 第二课时 单项式 课前自习 1. 单项式：即由_________与______的乘积组成的代数式称为单项式。例如： 2-3100 -4t p mn a y， ， ， 补充： 单独_________或___________也是单项式，如 a，5，0，-2，-ab 注：单项式是字母或数字的乘积而不是其它运算 例如： 5 5 5 5 5 1 54 4 ab ab m  可视为 所以它是单项式，而 、x+1、5-s只能理解为 m( 出以m）、x加 、减s 数字和字母间不是乘法运算，所以不能称为单项式。 练习：判断下列各代数式哪些是单项式？ (1) 2 1x ； (2)abc； (3)b2； (4)－5ab2； (5)y+x； (6)－xy2； (7)－5。 解：是单项式的有(填序号)：________________________ 3. 单项式的系数和次数 A：单项式的系数说的是单项式的数字， 例如： 2 3 - 25 - 5- 12 4 3 3 a b p a mb s    中，字母是（ ）数字是（ ），所以这个单项式的系数就是： 25 同理： 的系数就是：（ ），而单项式 mn可视为1 mn，所以它的系数是： 而有些由单个数字组成的单项式，例如：8也是一个单项式它的系数就是它本身为（ ） 的系数是：（ ） 的系数是：（ ） 的系数是 60 m：（ ） 的系数是：（ ） 的系数是：（ ） 0的系数是：（ ） B：单项式的次数是指一个单项式中所有的字母次数的和 例如： 2 3 2 3 2 2 (_________) 2 +3= 2 0 0 0 6 a b a b a b mn s   这个单项式中字母 的次数是（ ）次，字母 的次数是 次。所以单项式 的次数是2 （ ）次。 那么，数字 的次数是多少呢？在现在我们只能规定一个非 数字的次数是 ，在八年级数学的有关知识 学习以后，我们才能知为什么是 次。 例如： 的系数是（ ），次数是（ ）次 的系数是（ ），次数是（ 64 5 5, mnp ）次 的系数是（ ），次数是（ ）次 的系数是（ ），次数是（ ）次 练习： 四个单项式 3 1 a2h，2πr，abc，－m 中，请说出它们的数字因数和字母因数分 别是什么？ 例题 P56 例 3 单项式 3 1 a2h 2πr abc －m 系数 次数 课后巩固练习 A 组 P57 练习 第 1、2 题 1.判断下列各代数式是否是单项式。如不是,请说明理由；如是，请指出它的系数 和次数。 ①x＋1； ② x 1 ； ③πr2； ④－ 2 3 a2b。 2.下面各题的判断是否正确？ ①－7xy2 的系数是 7；（ ） ②－x2y3 与 x3 没有系数；（ ） ③－ab3c2 的次数是 0＋8＋2；（ ） ④－a3 的系数是－1；（ ） ⑤－32x2y3 的次数是 7；（ ） ⑥ 3 1 πr2h 的系数是 3 1 。（ ） 3.判断下列各代数式是否是单项式。如不是,请说明理由；如是，请指出它的系数 和次数。 ①x＋1； ② x 1 ； ③πr2； ④－ 2 3 a2b。 4.下面各题的判断是否正确？ ①－7xy2 的系数是 7；（ ） ②－x2y3 与 x3 没有系数；（ ） ③－ab3c2 的次数是 0＋8＋2；（ ） ④－a3 的系数是－1；（ ） ⑤－32x2y3 的次数是 7；（ ） ⑥ 3 1 πr2h 的系数是 3 1 。（ ） 5、 a 3 ，x＋1, －2， 3 b ， 0.72xy，各式中单项式的个数是（ ） A. 2 个 B.3 个 C.4 个 D.5 个 6、单项式－x2yz2 的系数、次数分别是（ ） A. 0，2 B. 0， 4 . C. －1，5 D.1，4 第三课时 多项式 课前自习 1.同学们我们上一节课学习了单项式，单项式是指数字或的乘积组成的式子，一 个单个的数字或字母也是一个单项式。你能写出三个单项式吗？ 例如： 2. 单项式有系数和次数，例如： 2 4 6 5 2.5 ab mn st   的系数是( )次数是（ ） 系数是( )次数是（ ） 系数是( )次数是（ ） 3. 多项式是由几个单项式的和组成的，每一个单项式称为这个多项式的 例如： 2 2 2 3 4 1 3 3 3 1 7 4 5 6 5 3 8 ( 6 ) 5 m st m pm s st xy m st xy            是一个多项式，它由3个单项式组成，这 个单项式称为这个多项式的项 所以这个多项式有 项，分别是： 、（ ）、 同理： 由（ ）个单项式组成，所以它有（ ）项，它们分别是 （ ）（ ）（ ） 如果一个多项式中有减号怎样看呢？可转化为加 例如： 8m 可视为： ( 3) -3   所以这个多项式共有4项，它们分别是：（ ）、（ ）、（ ）、（ ） 4. 和 统称为整式。 整式由多个单项式组成，所以它没有系数，但是多项式有次数，多项式次数以组 成它的单项式中次数最高的次数为多项式的次数。 例如： 2 4 2 2 4 2 7 9 3 3 5 1 4 3 5 1 1 2 2 5 3 3 4 0 5 4 5 4 -6 9 -5 s mn ab mn ab mn       这个多项式是由 项组成，它们是：3s 、 、 、 第 项是 次 第 项是 次 第 项是 次 第 项是 次 所以这个多项式的次数我们定为 次,又因为它由 项组成，所以这种多项式也称为 次 项式 同理： 多项式： st 它由（ ）个单项式组成，项分别是（ ）（ ）（ ），这些项 的次数分别是：（ ）次（ ）次（ ）次，最高次是：（ ）次，所以我们称这 个单项式的次数是:( )次，我们称它是（ ）次（ ）项式 例 1 例题解析： P58 练习 第 1、2 题 例 2 同学们在学习多项式时必须注意，一个多项式的“项”和“项的系数”是不一样 的概念例如： 2 2 2 2 2 2 2 4 3 2 5 4 1 3 3 5 4 1 0 3 5 4 1 3 5 5 mn s mn s mn s mn         这个多项式由 个单项式组成，所以它共有 项，分别是： 、 、 次数分别为3次、2次、次，所以我们称它为（ ）次（ ）项式， 这个多项式的 次项是： ，二次项是: ，常数项是：，但如果说写出它的 次项系数那就不是 ，而是写它的系数-5 -9x y-8m +10a -7这个多项式是（ ）次（ ）项式，它的 2 次项是（ ） 次项是：（ ）常数项是( ),3次项系数是（ ） 课后巩固练习 A 组 P59 习题 2.1 第 3 题 1．下列说法或书写正确的是 ①1x②-1x③a×3 ④a÷2 ⑤ 2 4 11 xy ⑥b 的系数为 1，次数为 0 ⑦ R2 的系数为 2，次数为 2 2．列代数式： (1)长方形的长与宽分别为 a、b，则长方形的周长是； (2)某班有男生 x 人，女生 21 人，则这个班共有学生人； (3)一个数比数 x 的 2 倍小 3，则这个数为_________； (4)鸡兔同笼，鸡 a 只，兔 b 只，则共有头个，脚只。 3. 多项式 523 2  xx 有_____项，它们是_________。其中常数项是________。 一个多项式含有几项，就叫几项式。多项式里_________________,叫做这个多项 式的次数。所以，多项式 523 2  xx 是一个____次______项式。 4. 下列说法中,正确的是( ) 5.－ 4 5 a2b－ 3 4 ab＋1 是次项式，其中三次项系数是，二次项为，常数项为，写出 所有的项。 6.如果 15  mxy 为四次单项式,则 m=____； B 组 1. P60 习题 2.1 第 6 题 2.下列关于 23 的次数说法正确的是( ) A. 2 次 B. 3 次 C. 0 次 D. 无法确定 第四课时 整式的加减法（一） 课前自习 1.同学们，在日常生活中我们会对一些事物分类，例如在扔拉圾时可回收和不可 回收的必须分类，再例如：2 只猫加 3 只猫应该等于 5 只猫，那么 3 只猫加 7 只狗 那应该等于（ ）猫？还是（ ）狗？同学们在填空时是不是会出遇到问 题，因为猫和狗不同类，整式的加法也是一样的，如果两个单项式不同类则无法 相加。 同理： ⑴ 6 个人+4 个人=⑵ 6 只羊+4 只羊= ⑶ 6 个人+4 只羊= （同学们得出答案吗？） 那么单项式中怎样才算同类呢？请同学们继续往下学习。 2.同类项 A：整式包括和，单项式中字母和字母的相同的单项式叫做同类项。 例如： 2 2 3 3 2 3 8 2 -2.5 4 6 4 mn mn c st s ae a e  与 这两个单项式的系数分别是（ ）和（ ），系数是不相同的 但是它们的字母都是相同的都是 m、n，m都是（ ）次，n都是 次 所以它们的字母和字母的次数都相同，那么它们称为同类项。 例如： ab与9ab，4b c与-b ，等等都是同类项 例如： 与 ，因为字母不同不是同类项 与 ，因为字母的次数不同所以不是同类项。 B：同类项必须字母和字母的次数都要相同，和系数没有关系，系数可以不同，但 字母和字母的相应次数一定要一样。两个数字（常数项）也是同类项。 例如： 3 和 -6 是同类项 练习： 判断下列说法是否正确，正确地在括号内打“√”，错误的打“×”。 (1)3x 与 3mx 是同类项。 ( ) (2)2ab 与－5ab 是同类项。 ( ) (3)3x2y 与－ 3 1 yx2 是同类项。 ( ) (4)5ab2 与－2ab2c 是同类项。 ( ) (5)23 与 32 是同类项。 ( ) 课后巩固练习 2 9,22 31,143 0,03,23 2 2 2 2   系数为的次数是单项式常数项是是三次三项式 次数是的系数是单项式次数是的系数是单项式 ab　　D、xyxC、 a　　　　　Ｂ、yxA、 A 组 1．下列各组式子中是同类项的是（ ）． A．-2a 与 a2 B．2a2b 与 3ab2 C．5ab2c 与-b2ac D．- 1 7 ab2 和 4ab2c 2、若 myx35 和 219 yxn 是同类项，则 m=_________,n=___________。 3、下列各组式子中，是同类项的是（ ） A、 yx 23 与 23xy B、 xy3 与 yx2 C、 x2 与 22x D、 xy5 与 yz5 4、在下列各组式子中，不是同类项的一组是（） A、 2 ，－5 B、－0.5xy2， 3x2y C、－3t，200πt D、 ab2，－b2a B 组 1.已知 15m x n 和－ 9 2 m 2 n 是同类项，则∣2－4x∣+∣4x－1∣的值为 （ ） A.1 B.3 C.8x－3 D.13 2、指出下列多项式中的同类项： (1)3x－2y＋1＋3y－2x－5； (2)3x2y－2xy2＋ 3 1 xy2－ 2 3 yx2； 3.若 45a b 与 22 x ya b 是同类项，则 x=, y=。 第五课时 整式的加法（二） -------- 合并同类项 课前自习 1.乘法分配律 2 2 (3 2) 4 (__________) 3 4 2 4 (_________) (3 2) 4 3 4 2 4 3 (_________)st                    这就是小学数学中我们学习过的乘法分配律 同理，整式的加法也是同样的： 例如： 3ab+6ab 这两个单项式是同类项，（字母和字母的次数相同） 3 ab+6 ab=(3+6) ab=(_______)(利用乘法分配律） 同理： 15st 把两个同类项的系数相加，字母和字母的次数不变，这就是我们这一节课学习的 合并同类项。 2.例题解析 P64 例 1 2 2 2 2 2 2 2 2 2 2 1(1) 5 1= ( )..............................5 11 ( ) ............................................5 (______) 2 2 3 2 xy xy xy xy xy xy y x y xy xy              解：原式 减法转化为加法：减去一个数等于加上它的相反数 合并同类项，系数相加减，字母和字母的次数不变 （ ）-3x 解 2 2 2 2 2 2 2 2 2 = 2 + 3 + 2 ......................... (__________)................................................................ 3 3 2 4 4 .. y x y xy xy x y b ab a b            ：原式 （-3x ）（ ）（ ） 分类：把是同类项的项放入一个括号 合并同类项，如果不是同类项，不能相加 （ ）4a 2 2 2 2 2 2 2 2 2 ................ 5 3 2 4 4 . = + 4 + 3 + 4 +2 =0+ b ab a b a b b ab           这个多项式有 项，4a 、 、 、 、 先把同类项放入一个括号 解：原式 （4a ）（ ） （ ）（ ） （-b ）+2ab =( ) 练习： P65 练习 第 1 题 例 2，先化简再求值 P64 例 2   2 2 2 2 2 2 2 5 4 3 2 = ( 3 ) ( 5 ) (4 ) 2...................................... 2..................................... 1 2 1= 2= - 2 (__________) 2 x x x x x x x x x x x                      解：原式 （2x ）+x 先把同类项分类写在括号中 合并同类项 当 时 原式 注：同学们在求式子值时必须先化简再求值，不能直接将数值代入原式，那样会很复杂也不合题意 例 2 的第二个例题和例 3 由同学们自己学习 练习： P65 练习 第 1、2、3、4 题 课后巩固练习 A 组 1.下列各题合并同类项的结果对不对？若不对，请改正。 (1)2x2＋3x2=5x4； (2)3x＋2y=5xy； (3)7x2－3x2=4； (4)9a2b－9ba2=0。 2.下列整式的运算中，结果正确的是 （ ） A.3+x＝3x B.y+y+y=y 3 C.6ab－ab=6 D.－ 4 1 st+0.25st=0 3．合并下列各式的同类项： （1）xy2- 1 5 xy2；（2）-3x2y+2x2y+3xy2-2xy2； （3）4a2+3b2+2ab-4a2-4b2（2） 22 24 xx  （3） 22 135 abab  （4） 3232 99 yxyx  B 组 1. 求多项式 3x2＋4x－2x2－x＋x2－3x－1 的值，其中 x=－3。 2．求多项式 a2b-6ab-3a2b+5ab+2a2b 的值，其中 a=0.1，b=0.01； 第六课时 整式的加减法（三） ------去括号 课前自习 1. 同学们，上一节课我们学习了合并同类项，能够将一些简单的多项式化简，如 果一个多项式中含有括号，那应该先去掉括号，这一节课，我们来学习去括号 化简多项式。 2. 去括号的原理是乘法分配律 例如： ( 3) +1 ( 3) ( 3) -1 3 ( ) ( 3) ( ) 3 3 X -3 +3. x x x x x x                        可视为： （x-3）=1 x-1 3=x-3 x-3 从形式上我们可看出括号前是正号时，去括号后原括号中的符号不变 可视为： （x-3）=(-1) x-(-1) 从形式上我们可看出括号前是负号时，去括号后原括号中的符号都会改变 原括号中 是正号，去括号后变为了负号，原括号中 是负数，去括号后变为 3. 利用去括号化简整式   4 P66 1 = = + .......................................... (_________)...................................... 例 （ ）8a+2b+(5a-b) 解：原式 8a+2b+5a-b......................括号前是正号，去括号后原括号中的各项符号不变 （8a+5a） 2b+(-b) 将多项式中的同类项分类 2 2 2 ......................... 2 =5 3 (3 6 )............................... 3 3 5 3 3 6 ........................ a b a b a b a b         合并同类项 （ ）(5a-3b)-3(a -2b) 解：原式 第一个括号前是“ ”号（省略了），去了括号后括号中不变号 第二个括号前是负号，而且有系数 ，应该先把系数 用乘法分配律乘入括号中。   2 ........................ ( 3 ) 6 5 3 ......................................... (_______________)............................................. b b a a        第二个括号前是“ ”号，去括号时括号中的每一项都应该变号 把同类的单项式分入一个括号 合并同类项 4. 去括号时强调：括号内每一项都要乘以 2，括号前是负因数时，去掉括号后， 括号内每一项都要变号．为了防止出错，可以先用分配律将数字 2与括号内的各 项相乘，然后再去括号，熟练后，再省去这一步，直接去括号。 例 5. 自学例 5 P67 练习：P67 练习第 1、2 题 课后巩固练习 A 组 P70 习题 2.2 第 1、2、5 题 B 组 1．下列各式化简正确的是（ ）。 A．a-（2a-b+c）=-a-b+c B．（a+b）-（-b+c）=a+2b+c C．3a-[5b-（2c-a）]=2a-5b+2c D．a-（b+c）-d=a-b+c-d 2．下面去括号错误的是（ ）． A．a2-（a-b+c）=a2-a+b-c B．5+a-2（3a-5）=5+a-6a+5 C．3a- 1 3 （3a2- 2a）=3a-a2+ 2 3 a D．a3-（a2+b）=a3-a2-b 3.计算下列各式 （1）（2x-3y）+（5x+4y） （2）（8a-7b）-（4a-5b）． 4．计算：5xy2-[3xy2-（4xy2-2x2y）]+2x2y-xy2． （一般地，先去小括号，再去 中括号。） 5.一种笔记本的单价是 x（元），圆珠笔的单价是 y（元），小红买这种笔记本 3 本， 买圆珠笔 2 支；小明买这种笔记本 4 个，买圆珠笔 3 支，买这些笔记本和圆珠笔， 小红和小明共花费多少钱？ 第七课时 整式的加减法（四） 课前自习 1. 同学们前两节课我们学习了合并同类项和去括号的知识，这些是整式加减法运 算的的基础，这一节课我们一起来学习整式的加减法。 2. 整式的加减法主要可分三个步骤： A：去括号，将式子中的所有括号去掉，如果有中括号的先去中括号，再去小括号， 去括号时同学们先注意括号前的符号，判断是否需要变号。 B ：将式子中的同类项分类写入一个括号中。 C：合并同类项 例如：   6 (1)(2 3 ) (5 4 ) 2 3 5 4 ....................................... + (2 5 ) ( 3 ) 4 ............................................ (________________)...... x y x y x y x y x x y y              例 解：原式 第一步去括号，两个括号前都 是 号，去括号后不变号 分类，将同类项分入一个括号中     .......................................... (2)(8 7 ) (4 5 ) 8 7 4 5 ....................................... + - 8 ( 4 ) ( 7 ) 5 ........................... a b a b a b a b a a a b              合并同类项 解：原式 第一个括号前是“”号，去掉后不变号，第二个括号前的是“”去掉后变号 ................ (____________________)............................................ 分类，将同类项分入一个括号中 合并同类项 练习： P69 练习 第 1、2 题 3. 化简求值 这是这一章的重点题型，同学们一定要先化简再求值，不能直接代入。代简其实 也就是先运算这个整式。 例如 P69 例 9 1 1 3 1 22 22( ) ( ) 2, . 2 3 2 3 3 1 2 3 12 2= (2 ) ( ).............................................2 3 2 3 1 2 3 12 22 ..............................................2 3 2 3 x x y x y x y x x y x y x x y x y                  求 的值，其中 解：原式 第一步，先把括号前的系数乘入括号中 ....................... 1 3 2 12 2( 2 ) ( ) ( ).....................................................2 2 3 3 (____________________________ x x x y y           第二步，去括号，第一个括号前是负号， 去掉后括号中每一项都要变号 第三步，分类，把同类项分入一个括号中， 代负号的项用小括号 ___)....................................................第四步，合并同类项 练习：P69 练习第 3 题 4. 自学互肋，由同学们自己合作讨论完成 P68 例 7、例 8 课后巩固练习 A 组 P70 习题 2.2 第 3、4、5、6、7、8 题 1．如果 a-b= 1 2 ，那么-（b-a）的值是（ ）． A．- 3 5 B． 2 3 C． 1 2 D． 1 6 2．一个多项式与 x2-2x+1 的和是 3x-2，则这个多项式为（ ）． A．x2-5x+3 B．-x2+x-1 C．-x2+5x-3 D．x2-5x-13 3．先化简再求值: 4x2y-[6xy-3（4xy-2）-x2y]+1，其中 x=2，y=- 1 2 ； 4．计算： （1）3（xy2-x2y）-2（xy+xy2）+3x2y； （2）5a2-[a2+（5a2-2a）-2（a2-3a）] B 组 P70 习题 2.2 第 7、8 题 5.求 1 2 x-2（x- 1 3 y2）+（- 3 2 x+ 1 3 y2）的值，其中 x=-2，y= 2 3 ． （思路点拨：先去括号，合并同类项化简后，再代入数值进行计算比较简便，去 括号时，特别注意符号问题。） 第八课时 整式的加减法复习课 课前自习 1、______和______统称整式。 （1）单项式：由与的乘积．．式子称为单项式。单独一个数或一个字母也是单项式， 如 a ，5。 单项式的系数：单式项里的叫做单项式的系数 单项式的次数：单项式中叫做单项式的次数 （2）多项式:几个的和叫做多项式。其中，每个单项式叫做多项式的，不含字母 的项叫做。 多项式的次数：多项式里的次数，叫做多项式的次数 2、同类项：必须同时具备的两个条件（缺一不可）： ①所含的相同； ②相同也相同 合并同类项，就是把多项式中的同类项合并成一项。 方法：把各项的相加，而不变。 3、去括号法则 法则 1: 法则 2: 去括号法则的依据实际是。 4、整式的加减 整式的加减的运算法则：如遇到括号，则先，再； 5、本章需要注意的几个问题 ①整式（既单项式和多项式）中，分母一律不能含有字母。 ②π不是字母，而是一个数字， ③多项式相加（减）时，必须用括号把多项式括起来，才能进行计算。 ④去括号时，要特别注意括号前面的因数。如果有因数时需先将这个因数乘入括 号中，再去括号。 课后巩固练习 A 组 1、在 3 2 2 21 1 2, 3, 1, , , ,4 , ,4 3xy x x y m n x abx x        ,  2b 中，单项式有： 多项式有：，整式有： . 2、已知-7x2ym 是 7 次单项式则 m= 4．单项式－ 6 5 2 yx 的系数是，次数是； 5.已知-5xmy3 与 4x3yn 能合并，则 mn = 。 6、7-2xy-3x2y3+5x3y2z-9x4y3z2 是次项式，其中最高次项是，最高次项的系数是，常 数项是，是按字母作幂排列。 7、已知 A=3x+1,B=6x-3，则 3A-B=。 8．已知单项式 3 2ba m 与－ 3 2 14 nba 的和是单项式，那么 m ＝，n＝ 9．化简 3 x －2（ x －3 y ）的结果是． 10．已知轮船在逆水中前进的速度是 m 千米/时，水流的速度是 2 千米/时，则这 轮船在静水中航行的速度是千米/时。 11、在下列代数式： xyxabcab 3,,0,3 2,4,3  中，单项式有（ ） A．3 个 B．4 个 C．5 个 D．6 个 12、下列各项式中，是二次三项式的是 （ ） A、 22 ba  B、 7 yx C、 25 yx  D、 222 3xxyx  13、下面计算正确的是（ ） Ａ．3 2x － 2x =3 Ｂ．3 2a ＋2 3a =5 5a Ｃ．3＋ x =3 x Ｄ．－0.25 ab ＋ 4 1 ba =0 14、化简 ( )m n m n   的结果为（ ） A． 2m B． 2m C． 2n D． 2n 15、三个连续奇数的第一个是 n,则三个连续奇数的和是 （ ） A、 n3 B、 33 n C、 63 n D、 43 n 16、化简下列各式。（每小题 7 分，共 14 分） （1） 2 2 28 [4 2 (2 5 )]m m m m m    （2） )5(3)8( 2222 xyyxyxxy  ； 17．电影院第 1 排有 a 个座位，后面每排都比前一排多 1 个座位，第 2 排有多少 个座位？第 3 排呢？用 m 表示第 n 排座位数，m 是多少？当 a=20，n=19 时，计算 m 的值． 18、某中学 3 名老师带 18 名学生，门票每张ａ元，有两种购买方式：第一种是老 师每人ａ元，学生半价；第二种是不论老师学生一律七五折，请你帮他们算一下， 按哪种方式购买门票比较省钱。 19．大客车上原有 (3 )m n 人，中途有一半人下车，又上车若干人，此时车上共 有乘客 (8 5 )m n 人，请问中途上车的共有多少人？当 10, 8m n  时，中途上车 的乘客有多少人？ B 组 1、“ x 的平方与 2 的差”用代数式表示为___________。 2、单项式 2 5 12 R 的系数是___________ ，次数是______________。 3、多项式 253 2  xx 是________次_________项式,常数项是___________。 4、若 myx35 和 219 yxn 是同类项，则 m=_________,n=___________。 5 、 与 多 项 式 22 357 baba  的 和 是 22 743 baba  的 多 项 式 是 ______________。 6、飞机的无风飞行航速为 a 千米/时，风速为 20 千米/时.则飞机顺风飞行 4 小时 的行程是__________千米；飞机逆风飞行 3 小时的行程是__________千米。 7、先化简，再求值.（每小题 10 分，共 20 分） （1） 2 2 23 (4 2 1) 2(3 1)a a a a a      ，其中 1 2a   ； （2） 2,2 3),3 1 2 3()3 1 4 1(2 22  yxyxyxx 其中 ； 8、（10 分）有这样一道题： “ 2, 2a b   时， 求多项式 3 3 2 3 3 2 21 13 42 4a b a b b a b a b b        22 3b  3 3 21 4a b a b     的值”，马小虎做题时把 2a  错抄成 2a   ，王小真没抄错 题，但他们做出的结果却都一样，你知道这是怎么回事吗？说明理由． 9 ． 有 这 样 一 道 题 ： “ 当 0.35, 0.28a b   时 ， 求 多 项 式 3 3 2 37 6 3 3a a b a b a   3 26 3a b a b  310a 的值.”有一位同学指出，题目中给 出的条件 0.35a  与 0.28b   是多余的，他的说法有道理吗？请加以说明。