初中数学中考复习课件章节考点专题突破：第七章 图形变化 考点突破30 图形的平移

初中数学中考复习课件章节考点专题突破：第七章 图形变化 考点突破30 图形的平移

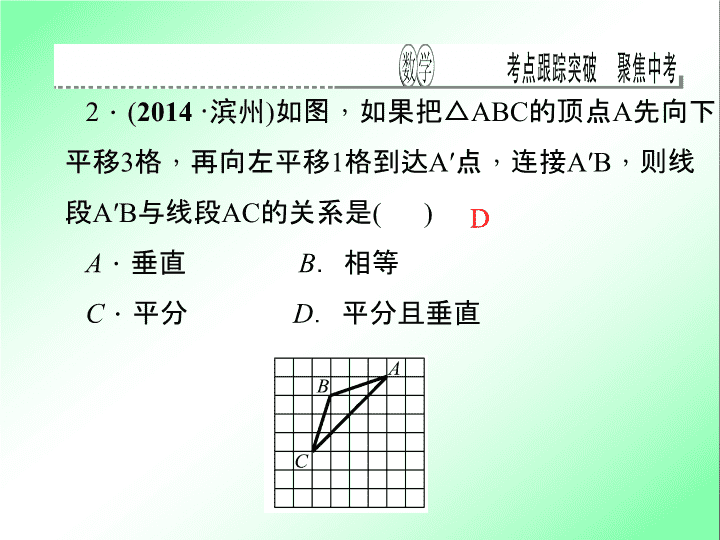
考点跟踪突破 30 　图形的平移 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 呼和浩特 ) 已知线段 CD 是由线段 AB 平移得到的， 点 A( － 1 ， 4) 的对应点为 C(4 ， 7) ， 则点 B( － 4 ， － 1) 的对应点 D 的坐标为 ( ) A ． (1 ， 2) B ． (2 ， 9) C ． (5 ， 3) D ． ( － 9 ， － 4) A 2 ． ( 2014 · 滨州 ) 如图 ， 如果把 △ ABC 的顶点 A 先向下平移 3 格 ， 再向左平移 1 格到达 A′ 点 ， 连接 A′B ， 则线段 A′B 与线段 AC 的关系是 ( ) A ． 垂直 B ．相等 C ． 平分 D ．平分且垂直 D 3 ． ( 2014 · 邵阳 ) 某数学兴趣小组开展动手操作活动， 设计了如图所示的三种图形 ， 现计划用铁丝按照图形制作相应的造型 ， 则所用铁丝的长度关系是 ( ) A ． 甲种方案所用铁丝最长 B ． 乙种方案所用铁丝最长 C ． 丙种方案所用铁丝最长 D ． 三种方案所用铁丝一样长 D 4 ． ( 2014 · 舟山 ) 如图 ， 将 △ ABC 沿 BC 方向平移 2 cm 得到 △ DEF ， 若 △ ABC 的周长为 16 cm ， 则四边形 ABFD 的周长为 ( ) A ． 16 cm B ． 18 cm C ． 20 cm D ． 22 cm C 5 ． ( 2013 · 滨州 ) 如图 ， 等边 △ ABC 沿射线 BC 向右平移到 △ DCE 的位置 ， 连接 AD ， BD ， 则下列结论： ① AD ＝ BC ； ② BD ， AC 互相平分； ③ 四边形 ACED 是菱形． 其中正确的个数有 ( ) A ． 0 个 B ． 1 个 C ． 2 个 D ． 3 个 D 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014 · 宜宾 ) 在平面直角坐标系中 ， 将点 A( － 1 ， 2) 向右平移 3 个单位长度得到点 B ， 则点 B 关于 x 轴的对称点 C 的坐标是 ． (2 ， - 2) 7 ． 如图 ， 将等腰直角 △ ABC 沿 BC 方向平移得到 △ A 1 B 1 C 1 . 若 BC ＝ 3 2 ， △ ABC 与 △ A 1 B 1 C 1 重叠部分的面积为 2 ， 则 BB 1 ＝ __ __ ． 8 ． ( 2012 · 无锡 ) 如图 ， △ ABC 中 ， ∠ ACB ＝ 90° ， AB ＝ 8 cm ， D 是 AB 的中点．现将△ BCD 沿 BA 方向平移 1 cm ， 得到△ EFG ， FG 交 AC 于点 H ， 则 GH 的长等于 ____ cm . 3 9 ． 如图 ① ， 两个等边 △ ABD ， △ CBD 的边长均为 1 ， 将 △ ABD 沿 AC 方向向右平移到 △ A′B′D′ 的位置得到图 ② ， 则阴影部分的周长为 ____ ． 2 10 ． ( 2012· 广安 ) 如图 ， 把抛物线 y ＝ 1 2 x 2 平移得到抛物线 m ， 抛物线 m 经过点 A ( － 6 ， 0 ) 和原点 O ( 0 ， 0 ) ， 它的顶点为 P ， 它的对称轴与抛物线 y ＝ 1 2 x 2 交于点 Q ， 则图中阴影部 分的面积为 __ __ ． 三、解答题 ( 共 40 分 ) 11 ． (10 分 ) ( 2013 · 云南 ) 如图 ， 下列网格中 ， 每个小正方形的边长都是 1 ， 图中 “ 鱼 ” 的各个顶点都在格点上． (1) 把 “ 鱼 ” 向右平移 5 个单位长度 ， 并画出平移后的图形； (2) 写出 A ， B ， C 三点平移后的对应点 A′ ， B′ ， C′ 的坐标． 12 ． (10 分 ) ( 2014 · 湘潭 ) 在边长为 1 的小正方形网格中 ， △ AOB 的顶点均在格点上． (1)B 点关于 y 轴的对称点坐标为 ； 解： (1)B 点关于 y 轴的对称点坐标为 ( － 3 ， 2) ( － 3 ， 2) (2) 将 △ AOB 向左平移 3 个单位长度得到 △ A 1 O 1 B 1 ， 请画出 △ A 1 O 1 B 1 ； (3) 在 (2) 的条件下 ， A 1 的坐标为 ． (3)A 1 的坐标为 ( － 2 ， 3) ( － 2 ， 3) 13 ． (10 分 ) ( 2014 · 珠海 ) 如图 ， 在 Rt △ ABC 中 ， ∠ BAC ＝ 90° ， AB ＝ 4 ， AC ＝ 3 ， 线段 AB 为半圆 O 的直径 ， 将 Rt △ ABC 沿射线 AB 方向平移 ， 使斜边与半圆 O 相切于点 G ， 得到 △ DEF ， DF 与 BC 交于点 H. (1) 求 BE 的长； (2) 求 Rt △ ABC 与 △ DEF 重叠 ( 阴影 ) 部分的面积． 解： (1) 连接 OG ， 如图 ， ∵∠ BAC ＝ 90 ° ， AB ＝ 4 ， AC ＝ 3 ， ∴ BC ＝ AB 2 ＋ AC 2 ＝ 5 ， ∵ Rt △ ABC 沿射线 AB 方向平移 ， 使斜边与半圆 O 相切于点 G ， 得 △ DEF ， ∴ AD ＝ BE ， DF ＝ AC ＝ 3 ， EF ＝ BC ＝ 5 ， ∠ EDF ＝ ∠ BAC ＝ 90 ° ， ∵ EF 与半圆 O 相切于点 G ， ∴ OG ⊥ EF ， ∵ AB ＝ 4 ， 线段 AB 为半圆 O 的直径 ， ∴ OB ＝ OG ＝ 2 ， ∵∠ GEO ＝ ∠ DEF ， ∴ Rt △ EOG ∽ Rt △ EFD ， ∴ OE EF ＝ OG DF ， 即 OE 5 ＝ 2 3 ， 解得 OE ＝ 10 3 ， ∴ BE ＝ OE － OB ＝ 10 3 － 2 ＝ 4 3 (2)BD ＝ DE － BE ＝ 4 － 4 3 ＝ 8 3 . ∵ DF ∥ AC ， ∴ DH AC ＝ BD AB ， 即 DH 3 ＝ 8 3 4 ， 解得 DH ＝ 2. ∴ S 阴影 ＝ S △ BDH ＝ 1 2 BD·DH ＝ 1 2 × 8 3 × 2 ＝ 8 3 ， 即 Rt △ ABC 与 △ DEF 重叠 ( 阴影 ) 部分的面积为 8 3 14 ． ( 10 分 ) ( 2013· 绍兴 ) 如图 ， 矩形 ABCD 中 ， AB ＝ 6 ， 第 1 次平移 将矩形 ABCD 沿 AB 的方向向右平移 5 个单位 ， 得到矩形 A 1 B 1 C 1 D 1 ， 第 2 次平移将矩形 A 1 B 1 C 1 D 1 沿 A 1 B 1 的方向向 右平移 5 个单位 ， 得 到矩形 A 2 B 2 C 2 D 2 ， … ， 第 n 次平移将矩形 A n － 1 B n － 1 C n － 1 Dn － 1 沿 A n － 1 B n － 1 的方向平移 5 个单位 ， 得到矩形 A n B n C n D n ( n ＞ 2 ) ． ( 1 ) 求 AB 1 和 AB 2 的长； ( 2 ) 若 AB n 的长为 56 ， 求 n. 解： (1) ∵ AB ＝ 6 ， 第 1 次平移将矩形 ABCD 沿 AB 的方向向右平移 5 个单位 ， 得到矩形 A 1 B 1 C 1 D 1 ， 第 2 次平移将矩形 A 1 B 1 C 1 D 1 沿 A 1 B 1 的方向向右平移 5 个单位 ， 得到矩形 A 2 B 2 C 2 D 2 … ∴ AA 1 ＝ 5 ， A 1 A 2 ＝ 5 ， A 2 B 1 ＝ A 1 B 1 － A 1 A 2 ＝ 6 － 5 ＝ 1 ， ∴ AB 1 ＝ AA 1 ＋ A 1 A 2 ＋ A 2 B 1 ＝ 5 ＋ 5 ＋ 1 ＝ 11 ， ∴ AB 2 的长为 5 ＋ 5 ＋ 6 ＝ 16 (2) ∵ AB 1 ＝ 2 × 5 ＋ 1 ＝ 11 ， AB 2 ＝ 3 × 5 ＋ 1 ＝ 16 ， ∴ AB n ＝ (n ＋ 1) × 5 ＋ 1 ＝ 56 ， 解得 n ＝ 10