2020年河北省唐山市开平区中考数学一模试卷 (含解析)

2020年河北省唐山市开平区中考数学一模试卷 (含解析)

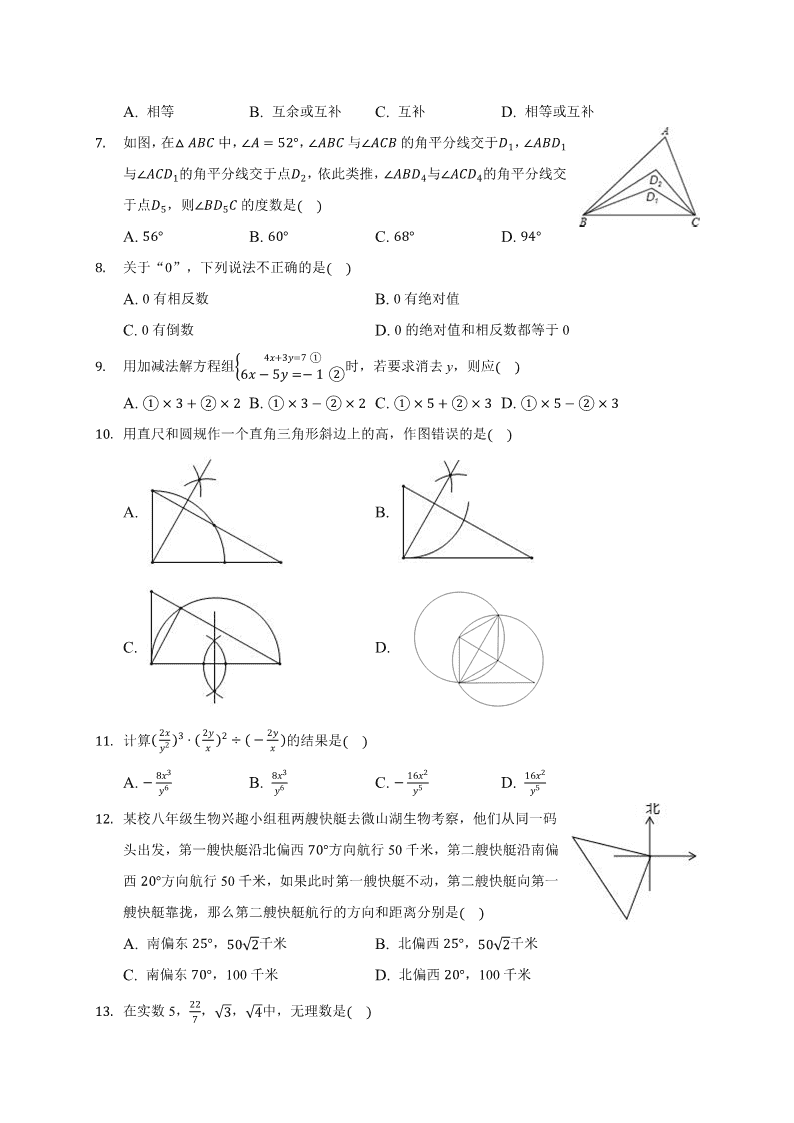
2020年河北省唐山市开平区中考数学一模试卷一、选择题（本大题共16小题，共42.0分）1.下列各组运算中，其值最小的是A.B.C.D..如图所示的几何体是由5个大小相同的小立方块搭成，它的主视图是A.B.C.D..若，，则A.12B.4C.32D.2.下列说法正确的是A.为了解一批灯泡的使用寿命，宜采用普查方式1B.掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为C.掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件香.，D.甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是甲乙香.䁣，则甲的射击成绩较稳定͵香5.已知不等式组，其解集在数轴上表示正确的是1香A.B.C.D.䁣.如果和的两边分别平行，那么和的关系是 A.相等B.互余或互补C.互补D.相等或互补7.如图，在中，5，与的角平分线交于1，1与1的角平分线交于点，依此类推，与的角平分线交于点5，则5的度数是A.5䁣B.䁣香C.䁣D..关于“0”，下列说法不正确的是A.0有相反数B.0有绝对值C.0有倒数D.0的绝对值和相反数都等于0t7①.用加减法解方程组时，若要求消去y，则应䁣5t1②A.①②B.①②C.①5②D.①5②1香.用直尺和圆规作一个直角三角形斜边上的高，作图错误的是A.B.C.D.tt11.计算的结果是t1䁣1䁣A.t䁣B.t䁣C.t5D.t51.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察，他们从同一码头出发，第一艘快艇沿北偏西7香方向航行50千米，第二艘快艇沿南偏西香方向航行50千米，如果此时第一艘快艇不动，第二艘快艇向第一艘快艇靠拢，那么第二艘快艇航行的方向和距离分别是A.南偏东5，5香千米B.北偏西5，5香千米C.南偏东7香，100千米D.北偏西香，100千米1.在实数5，，，中，无理数是7 A.5B.C.D.71.点11t1，点t是一次函数t图象上的两个点，且1香，则t1与t的大小关系是A.tt1B.t1͵t͵C.t1tD.t1t͵15.如图，在中，香，，垂足为D，，垂足为E，则图中与相似的三角形个数为A.1B.2C.3D.41䁣.在平面直角坐标系中有二次函数t，点1t1，t是该二次函数图象上的两点，其中1香，则下列结论正确的是A.t1tB.t1͵tC.y的最小值是D.y的最小值是二、填空题（本大题共3小题，共11.0分）17.分解因式______．1111.一根长为2020厘米的塑料管，第1次截去全长的，第2次截去剩下的，第3次截去剩下的，1如此下去，直到第2019次截去剩下的，则最后剩下的塑料管长为_________厘米．香香1.若菱形的两条对角线分别为10和24，则该菱形的边长是_________，菱形的面积是______，菱形的高是___________．三、解答题（本大题共7小题，共67.0分）香.读下列材料，解决材料后的问题：【材料1】最小公倍数ൌͶൌൌݐͶݑ是一种数学概念，是指两个或多个整数公有的倍数中，除0以外最小的一个公倍数． 【材料2】最小公倍数的计算方法：利用短除法，借助最大公约数来计算：例如：求96和132的最小公倍数．【应用】1试着模仿【材料2】用短除法求16和24的最小公倍数；小文的爸爸和妈妈都是医务工作者，在疫情期间他们都参与到抗疫工作中，都不能按双休日休息.其中爸爸每工作14天休息一天，妈妈每工作8天休息一天，2020年2月1日这天，爸爸和妈妈恰好同时休息，那么下次两人同时休息是在_____年_____月____日.友情提示：2020年2月有29天21.为了发展乡村旅游，建设美丽从化，某中学七年级一班同学都积极参加了植树活动，今年四月份该班同学的植树情况部分如图所示，且植树2株的人数占︀．1求该班的总人数、植树株数的众数，并把条形统计图补充完整；若将该班同学的植树人数所占比例绘制成扇形统计图时，求“植树3株”对应扇形的圆心角的度数；求从该班参加植树的学生中任意抽取一名，其植树株数超过该班植树株数的平均数的概率． 22.观察不等式：11，5，75，71用含有字母1且为整数的等式表示这一规律；请用所学知识验证这个规律的正确性；借助你发现的规律把400写成两个正整数的平方差的形式：香香____________．23.在平面直角坐标系中，点O是坐标原点，矩形OABC的边OA、OC分别在x轴和y轴上，，；点D是BC的四等分点，且.反比例函数t͵香的图象经过点D， 交AB于点.连接OE、OB．1求反比例函数的解析式；求的面积．24.如图，M、N是边长为6的正方形ABCD的边CD上的两个动点，满足，连接AC交BN于点E，连接DE交AM于点F，连接CF．1求证：；判断DE与AM的位置关系，并证明；判断线段CF是否存在最小值？若存在，求出来，若不存在，说明理由．25.一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，前2分钟其速度米分与时间Ͷ分满足二次函数Ͷ，后三分钟其速度米分与时间Ͷ分满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米分，求：1二次函数和反比例函数的关系式．弹珠在轨道上行驶的最大速度． 26.如图1，点O和矩形CDEF的边CD都在直线l上，以点O为圆心，以24为半径作半圆，分别交直线l于A，B两点．已知：1，ܨ，矩形自右向左在直线l上平移，当点D到达点A时，矩形停止运动．在平移过程中，设矩形对角线DF与半圆的交点为点P为半圆上远离点B的交点．1如图2，若FD与半圆相切，求OD的值；如图3，当DF与半圆有两个交点时，求线段PD的取值范围；若线段PD的长为20，直接写出此时OD的值． 【答案与解析】1.答案：A解析：本题考查了有理数的混合运算，顺序为：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．也考查了有理数大小比较．根据有理数的运算法则分别计算，再比较大小即可求解.解：.原式55，B.原式䁣，C.原式，D.原式.5，5.5䁣，最小的值为5．故选A．2.答案：D解析：解：如图所示的几何体的主视图是．故选：D．从正面看：共有2列，从左往右分别有1，2个小正方形；据此可画出图形．考查简单组合体的三视图；用到的知识点为：主视图，左视图，俯视图分别是从物体的正面，左面，上面看得到的图形．3.答案：C解析：本题主要考查了同底数幂的乘法法则，解决问题的关键是逆用同底数幂的乘法法则．同底数幂相乘，底数不变，指数相加．依据同底数幂的乘法法则进行计算即可． 解：，，．故选C．4.答案：D解析：解：A、为了解一批灯泡的使用寿命，宜采用抽样调查的方式，所以A选项错误；B、利用树状图得到共有正正、正反、反正、反反四种可能的结果数，所以两枚硬币都是正面朝上这1一事件发生的概率为，所以B选项错误；C、掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是随机事件，所以C选项错误；香.，香.䁣，所以甲的方差小于乙的方差，所以甲的射击成绩较稳定，所以D选D、因为甲乙项正确．故选：D．根据全面调查与抽样调查的特点对A进行判断；利用画树状图求概率可对B进行判断；根据必然事件和随机事件的定义对C进行判断；根据方差的意义对D进行判断．本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．也考查了统计的有关概念．5.答案：B͵香①解析：解：1香②解不等式①得：͵，解不等式②得：1，不等式组的解集为：͵，在数轴上表示不等式组的解集为：故选：B．求出每个不等式的解集，找出不等式组的解集，再在数轴上把不等式组的解集表示出来，即可得出选项． 本题考查了在数轴上表示不等式组的解集，解一元一次不等式组的应用，关键是能正确在数轴上表示不等式组的解集．6.答案：D解析：本题考查平行线的性质，主要利用两直线平行，同位角相等以及同旁内角互补作答．解：如图知和的关系是相等或互补．故选D．7.答案：A解析：此题主要考查角平分线的定义和三角形的内角和定理．根据三角形的内角和定理可得1香51，再根据角平分线的定义和三角形的内角和定理表示出1，，找到规律可求得5C.解：5，1香51，又与的角平分线交于1，1111，11，11111䁣，111香1香䁣11䁣，同理1香1香䁣，1依此类推，51香1香15䁣．故选A．8.答案：C解析： 1本题考查了倒数：a的倒数为香，也考查了相反数与绝对值．分别根据相反数、绝对值和倒数的定义判断．解：A、0的相反数为0，所以A选项的说法正确；B、0的绝对值为0，所以B选项的说法正确；C、0没有倒数，所以C选项的说法错误；D、0的绝对值和相反数都等于0，所以D选项的说法正确．故选C．9.答案：C解析：本题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．利用加减消元法消去y即可．t7①解：用加减法解方程组时，若要求消去y，则应①5②，䁣5t1②故选C．10.答案：B解析：本题考查了作图基本作图：熟练掌握基本作图作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线．根据基本作图对A、B、D进行判断；根据圆周角定理对C进行判断．解：A选项通过作线段的垂直平分线得到斜边上的高，C选项通过作90度的圆周角得到斜边上的高，D选项通过画图得到菱形，即可得到斜边上的高，B选项无法保证斜边所对的顶点在所画线段的垂直平分线上，故选：B．11.答案：C解析：本题考查分式的混合运算，在进行分式乘方运算时，先确定运算结果的符号，同时要注意运算顺序，先乘方，后乘除．分式的乘除混合运算一般是统一为乘法运算，如果有乘方，还应根据分式乘方法 则先乘方，即把分子、分母分别乘方，然后再进行乘除运算．同样要注意的地方有：一是要确定好结果的符号；二是运算顺序不能颠倒．根据分式的混合运算法则计算即可．tt解：ttt䁣t1䁣；t5故选C．12.答案：B解析：解：第一艘快艇沿北偏西7香方向，第二艘快艇沿南偏西香方向，香，5香，5香，5，第二艘快艇沿南偏西香方向，1香，5香5，第二艘快艇航行的方向和距离分别是：北偏西5，5香千米．故选：B．根据题意得出以及香，进而得出第二艘快艇航行的方向和距离．此题主要考查了方向角以及勾股定理，正确把握方向角的定义是解题关键．13.答案：C解析：此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像香.1香1香香1香香香1，等有这样规律的数．无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．解：是无理数，故选C． 14.答案：B解析：解：t中香，函数图象中y随x的增大而减小，点11t1，点t，香是一次函数t图象上的三个点，且1香，t1͵t͵，故选：B．先根据函数解析式和函数的性质得出函数图象中y随x的增大而减小，图象经过一、二、四象限，再得出答案即可．本题考查了一次函数的图象和性质、一次函数图象上点的坐标特征等知识点，能熟记一次函数的性质是解此题的关键．15.答案：D解析：本题考查了相似三角形的判定，是基础知识，要熟练掌握．根据题意得，则，从而得出∽，则，即可证明∽，∽，∽．解：，，香，香，，，∽，，∽，，，∽．香，， ∽．综上，图中与相似的三角形有4个．故选D．16.答案：D解析：本题考查了二次函数图象上点的坐标特征，二次函数的最值，解题时，利用了“数形结合”的数学思想．根据抛物线解析式求得抛物线的顶点坐标，结合函数图象的增减性进行解答．解：t1，则该抛物线与x轴的两交点横坐标分别是、1，又t1，该抛物线的顶点坐标是1，对称轴为1．A.无法确定点A、B离对称轴1的远近，故无法判断t1与t的大小，故本选项错误；B.无法确定点A、B离对称轴1的远近，故无法判断t1与t的大小，故本选项错误；C.y的最小值是，故本选项错误；D.y的最小值是，故本选项正确．故选D．17.答案：解析：解：原式．故答案为：．首先提取公因式a，再利用平方差公式分解因式得出答案．此题主要考查了提取公因式法以及公式法分解因式，正确应用公式是解题关键．18.答案：1解析： 本题考查了有理数的混合运算，正确列式是难点，掌握运算法则是解题的关键．根据题意得到算式111香香111，先计算括号里面的减法，再约分计算即可求解．香香111解：根据题意得，香香111香香1香1香香香香1厘米．即剩下的塑料管长为1厘米．故答案为1．1香19.答案：13；120；1解析：本题主要考查的是菱形的性质，勾股定理的有关知识，由菱形的性质以及两条对角线长可求出其边长；根据菱形的面积等于对角线乘积的一半即可求出该菱形的面积；继而求得菱形的高．解：菱形的两条对角线长分别为10和24，1该菱形的面积是：1香1香；该菱形的边长为：1香1，1香菱形的高．11香故答案为13，120，．120.答案：解：1，1䁣，24的最小公倍数为，香香；3；17解析：本题主要考查了有理数的运算，解答此题的关键是读懂材料，知道找最小公倍数的方法．1结合材料，用短除法求出最小公倍数即可；先找出15和9的最小公倍数为45，可得45天后为共同休息的时间，然后结合日历找出2月1 日后的第45天的日期即可．解：1见答案；1115天，1天，15和9的最小公倍数是：45，即再经过45天，爸爸、妈妈再次同时休息．香香年2月份共29天，故2月还有28天，517天故3月份第17天，爸爸和妈妈同时休息，即2020年3月17日，故答案为2020；3；17．21.答案：解：1该班的总人数：1䁣︀5香人；因为植3株的人数为5香1䁣71，数据2出现了16次，出现次数最多，所以植树株数的众数是2；条形统计图补充如图所示．因为植3株的人数为5香1䁣71人，且所占总人数比例：15香︀，“植树3株”对应扇形的圆心角的度数为：︀䁣香1香香.度；该班植树株数的平均数11䁣1755香.䁣，植树株数超过该班植树株数平均数的人数有：175人，5概率香.5．5香答：植树株数超过该班植树株数平均数的概率是香.5．解析：1植2株的有16人，所占百分比为︀，则可求出其总人数，根据计算结果结合图表找出众数；结合1的数据将条形统计图补充完整；先根据“植树3株”的人数为5香1䁣71人，且所占总人数比例：15香︀，即可得到“植树3株”对应扇形的圆心角的度数； 根据题意，求得其平均数为.䁣，超过平均数的为25人，根据概率公式进行计算即可．本题主要考查了条形统计图以及概率的计算，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．解题时注意：一组数据按顺序排列后，中间的那两个数的平均数或中间的那个数叫做中位数；概率所求情况数与总情况数之比．22.答案：解：1用含有字母1且为整数的等式表示这一规律：111且为整数；111111；1香1；99解析：此题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力，本题的关键规律是：11．1通过观察可发现两个连续奇数的平方差是8的倍数，第n个等式为：11；根据平方差公式即可求解；香香5香5香15香11香1．故答案为：101，99．23.答案：解：1四边形ABCO是矩形，，点D是BC的四等分点，且，，，，将点代入t得，反比例函数的解析式为：t；点E在AB上，将代入t得t1，1，1，， 11的面积1．解析：本题考查了用待定系数法求反比例函数的解析式、反比例函数系数k的几何意义、反比例函数图象上点的特征以及矩形的性质，是一道综合题，难度中等．1根据题意得出点D的坐标，从而可得出k的值；根据三角形的面积公式和点E在函数的图象上，即可得出结论．24.答案：1证明：在正方形ABCD中，，，又AE为公共边，≌，．解：结论：互相垂直．理由：：在正方形ABCD中，，香，，Ͷ≌Ͷൌ，由1知，又，CE为公共边，≌，ܨ香ܨܨ香ܨ1香香香即．存在最小值．如图，取AD的中点O，连接OF、OC， 1则ܨ，在Ͷ中，䁣5，根据三角形的三边关系，ܨܨ͵，当O、F、C三点共线时，CF的长度最小，最小值为ܨ5．解析：本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用三角形三边关系解决最值问题，属于中考压轴题．1证明≌即可解决问题．想办法证明即可．存在最小值．如图，取AD的中点O，连接OF、OC，利用三角形三边关系解决问题即可．25.答案：解：1Ͷ的图象经过点1，．二次函数的解析式为：Ͷ，香Ͷ；设反比例函数的解析式为，Ͷ由题意知，图象经过点，1䁣，1䁣反比例函数的解析式为Ͷ5；Ͷ由图可知弹珠在轨道上行驶的最大速度在2秒末，为8米分．解析：本题考查了反比例函数和二次函数的应用．解题的关键是从图中得到关键性的信息：自变量的取值范围和图象所经过的点的坐标．1由图象可知前一分钟过点1，后三分钟时过点，分别利用待定系数法可求得函数解析式；把Ͷ代入1中二次函数解析式即可．26.答案：解：1如图2，连接OP，ܨ与半圆相切， ܨ，香，在矩形CDEF中，ܨ香，1，ܨ，则ܨ1香，ܨ香，ܨ，ܨ，≌ܨ，ܨ香；如图3，当点B、D重合时，过点O作ܨ与点H，则，cos，ܨ而1，，由1知ܨ香，17，，香51则，5DF与半圆相切，由1知：1，11；5设半圆与矩形对角线交于点P、H，过点O作ܨ， 则，tanܨͶ，则ൌ，15设：，则：，香，，tanܨ香整理得：5䁣香11䁣香，䁣5解得：，5香51．cos5解析：1如图2，连接OP，则DF与半圆相切，利用≌ܨ，可得：ܨ香；71利用cos，求出，则；DF与半圆相切，由1知：ܨ551，即可求解；设：，则：，香，tanܨ，求出香䁣5，利用，即可求解．5cos本题考查的是圆的基本知识综合运用，涉及到直线与圆的位置关系、解直角三角形等知识，其中，正确画图，作等腰三角形OPH的高OG，是本题的关键．