苏教版数学九年级上册课件2-5直线与圆的位置关系（2）

苏教版数学九年级上册课件2-5直线与圆的位置关系（2）

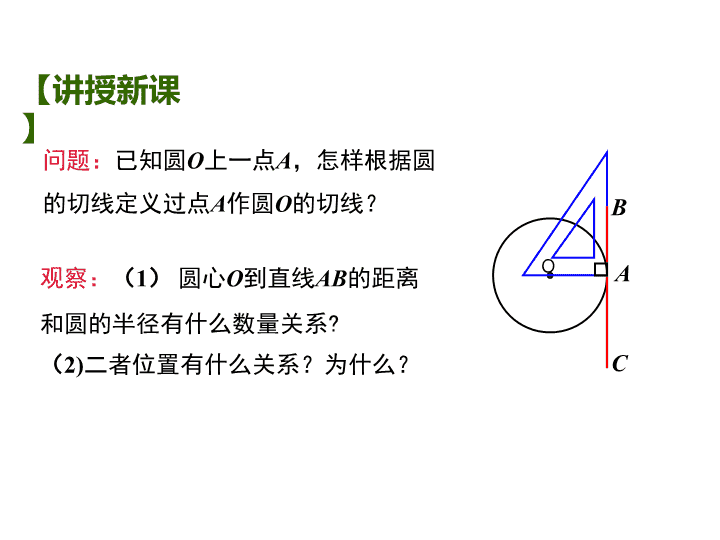
2.5直线与圆的位置关系（2） 砂轮上打磨工件时飞出的火星右图中让你感受到了直线与圆的哪种位置关系？【导入新课】 ＯABC问题：已知圆O上一点A，怎样根据圆的切线定义过点A作圆O的切线？观察：（1）圆心O到直线AB的距离和圆的半径有什么数量关系?（2)二者位置有什么关系？为什么？【讲授新课】 经过半径的外端并且垂直于这条半径的直线是圆的切线.OA为☉O的半径BC⊥OA于ABC为☉O的切线.ＯABC切线的判定定理应用格式 下列各直线是不是圆的切线？如果不是，请说明为什么？O.AO.ABAO(1)(2)(3)(1)不是，因为没有垂直.(2),(3)不是，因为没有经过半径的外端点A.在此定理中，“经过半径的外端”和“垂直于这条半径”，两个条件缺一不可，否则就不是圆的切线.注意判一判 判断一条直线是一个圆的切线有三个方法：1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；3.判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.lAlOlrd要点归纳 典例精析例1如图,直线AB是☉O上的点A,且AB=OA，∠OBA=45°,AT=BA．求证：直线AB是☉O的切线.解析：直线AB经过半径的一端，因此只要证OA垂直于AB即可.AOB证明：∵AB=OA，∠OAB＝45°，∴∠AOB＝∠OBA＝45°，∴∠OAB=90°.即OA⊥AB.又∵点A在圆上，∴直线AB是☉O的切线.（切线的判定定理） 如图,AB是☉O的直径,∠ABT=45°,AT=BA．求证:AT是☉O的切线.ATBO证明：∵AT=AB，∴∠ABT＝∠ATB，又∵∠ABT＝45°，∴∠ATB=45°.解析：AT经过直径的一端，因此只要证AT垂直于AB即可.∴AT是☉O的切线．∴∠TAB＝180°-∠ABT-∠ATB=90°.即AT⊥AB.做一做 思考：如图，如果直线l是☉O的切线，点A为切点，那么OA与l垂直吗？AlO∵直线l是☉O的切线，A是切点，∴直线l⊥OA.切线的性质切线的性质定理圆的切线垂直于经过切点的半径．应用格式 小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.（1）假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,（2）则OM

查看更多