人教版9年级上册数学全册导学案22_7 二次函数导学案

人教版9年级上册数学全册导学案22_7 二次函数导学案

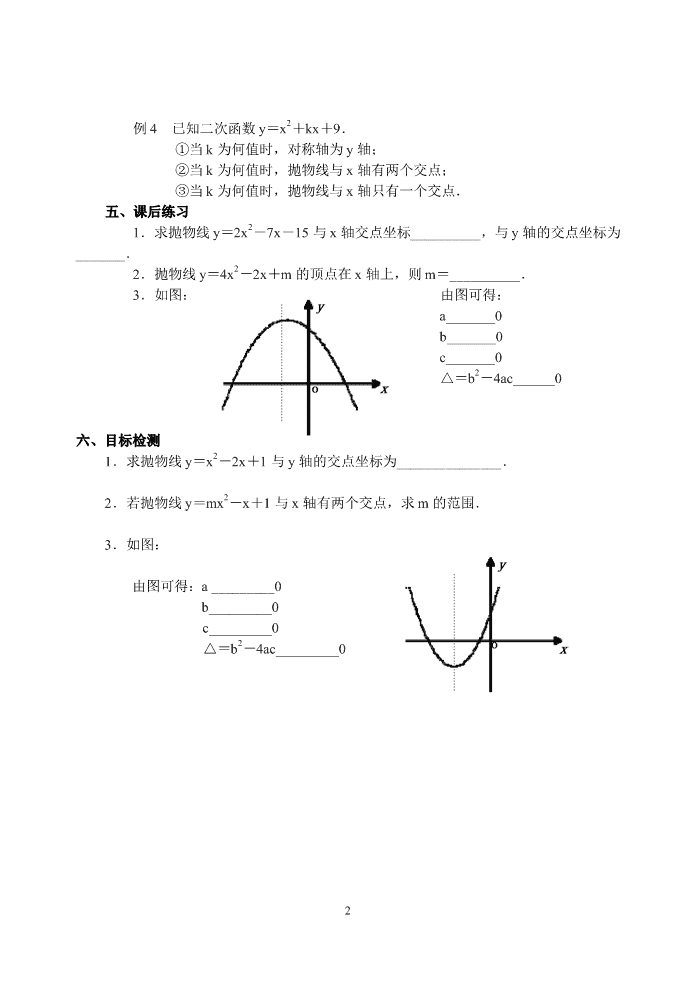
1 第二十二章 二次函数 第 7 课时 二次函数 y＝ax2＋bx＋c 的性质 一、复习知识点：第 6 课中“理一理知识点”的内容． 二、学习目标： 1．懂得求二次函数 y＝ax2＋bx＋c 与 x 轴、y 轴的交点的方法； 2．知道二次函数中 a，b，c 以及△＝b2－4ac 对图象的影响． 三、基本知识练习 1．求二次函数 y＝x2＋3x－4 与 y 轴的交点坐标为_______________，与 x 轴的交点坐 标____________． 2．二次函数 y＝x2＋3x－4 的顶点坐标为______________，对称轴为______________． 3．一元二次方程 x2＋3x－4＝0 的根的判别式△＝______________． 4．二次函数 y＝x2＋bx 过点（1，4），则 b＝________________． 5．一元二次方程 y＝ax2＋bx＋c（a≠0）， △＞0 时，一元二次方程有_______________， △＝0 时，一元二次方程有___________，△＜0 时，一元二次方程_______________． 四、知识点应用 1．求二次函数 y＝ax2＋bx＋c 与 x 轴交点（含 y＝0 时，则在函数值 y＝0 时，x 的值 是抛物 线与 x 轴交点的横坐标）． 例 1 求 y＝x2－2x－3 与 x 轴交点坐标． 2．求二次函数 y＝ax2＋bx＋c 与 y 轴交点（含 x＝0 时，则 y 的值是抛物线与 y 轴交点 的纵 坐标）． 例 2 求抛物线 y＝x2－2x－3 与 y 轴交点坐标． 3．a、b、c 以及△＝b2－4ac 对图象的影响． （1）a 决定：开口方向、形状 （2）c 决定与 y 轴的交点为（0，c） （3）b 与－ b 2a 共同决定 b 的正负性 （4）△＝b2－4ac       轴没有交点与 轴有一个交点与 轴有两个交点与 x x x 0 0 0 例 3 如图， 由图可得： a_______0 b_______0 c_______0 △______0 2 例 4 已知二次函数 y＝x2＋kx＋9． ①当 k 为何值时，对称轴为 y 轴； ②当 k 为何值时，抛物线与 x 轴有两个交点； ③当 k 为何值时，抛物线与 x 轴只有一个交点． 五、课后练习 1．求抛物线 y＝2x2－7x－15 与 x 轴交点坐标__________，与 y 轴的交点坐标为 _______． 2．抛物线 y＝4x2－2x＋m 的顶点在 x 轴上，则 m＝__________． 3．如图： 由图可得： a_______0 b_______0 c_______0 △＝b2－4ac______0 六、目标检测 1．求抛物线 y＝x2－2x＋1 与 y 轴的交点坐标为_______________． 2．若抛物线 y＝mx2－x＋1 与 x 轴有两个交点，求 m 的范围． 3．如图： 由图可得：a _________0 b_________0 c_________0 △＝b2－4ac_________0