初中数学中考复习课件章节考点专题突破：第六章 图形性质2 第25讲 直线与圆的位置关系

初中数学中考复习课件章节考点专题突破：第六章 图形性质2 第25讲 直线与圆的位置关系

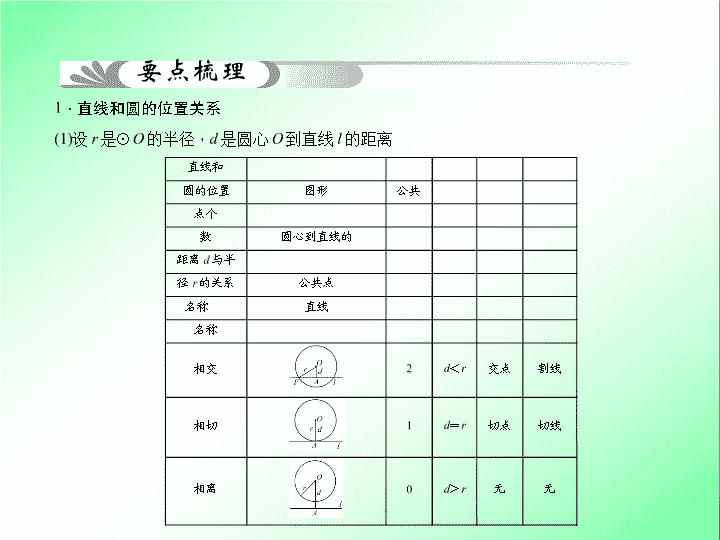
人教 数 学 第六章　图形的性质 ( 二 ) 第 25 讲　直线与圆的位置关系 要点梳理 1 ． 直线和圆的位置关系 (1) 设 r 是 ⊙ O 的半径 ， d 是圆心 O 到直线 l 的距离 直线和 圆的位置 图形 公共 点个 数 圆心到直线的 距离 d 与半 径 r 的关系 公共点 名称 直线 名称 相交 2 d ＜ r 交点 割 线 相切 1 d ＝ r 切点 切线 相离 0 d ＞ r 无 无 要点梳理 (2) 切线的性质： ① 切线的性质定理：圆的切线 经过切点的半径． ② 推论 1 ：经过切点且垂直于切线的直线必经过 ． ③ 推论 2 ：经过圆心且垂直于切线的直线必经过 ． 垂直于 圆心 切点 要点梳理 (3) 切线的判定定理：经过半径的外端并且 这条半径的直线是圆的切线． (4) 三角形的内切圆：和三角形三边都 的圆叫做三角形的内切圆 ， 内切圆的圆心是 ， 内切圆的圆心叫做三角形的 ， 内切圆的半径是内心到三边的距离 ， 且在三角形内部． 垂直于 相切 三角形三条角平分线的交点 内心 要点梳理 2 ． 相关辅助线 两种方法： 欲证直线为圆的切线时： (1) 若知道直线和圆有公共点时 ， 常连接公共点和圆心 ， 证明直线垂直半径； (2) 不知道直线和圆有公共点时 ， 常过圆心向直线作垂线 ， 证明垂线段的长等于圆的半径． 两个防范： (1) 直线和圆有一个公共点 ， 则直线与圆相切． 分析：直线和圆有一个公共点 ， 不排除还有另一个公共点． 正确说法：直线和圆有且只有一个公共点 ， 则直线与圆相切． (2) 圆的切线垂直于圆的半径． 分析：圆的半径有无数条 ， 切线垂直于哪条半径呢？ 正确说法：圆的切线垂直于过切点的半径． 一种分类思想 圆是一种极为重要的几何图形 ， 由于图形位置、形状及大小的不确定 ， 经常出现多结论情况．解题时漏解出错时有发生 ， 解决这类问题 ， 一定要仔细分析 ， 缜密思考 ， 分类讨论 ， 逐一解答 ， 切忌因思维定势或考虑不周而造成漏解． (1) 由于点在圆周上的位置的不确定而分类讨论； (2) 由于弦所对弧的优劣情况的不确定而分类讨论； (3) 由于弦的位置不确定而分类讨论； (4) 由于直线与圆的位置关系的不确定而分类讨论． 1 ． ( 2014 · 临夏州 ) 已知 ⊙ O 的半径是 6 cm ， 点 O 到同一平面内直线 l 的距离为 5 cm ， 则直线 l 与 ⊙ O 的位置关系是 ( ) A ． 相交　　　 B ．相切　　　 C ．相离　　 D ．无法判断 A 2 ． ( 2014 · 哈尔滨 ) 如图 ， AB 是 ⊙ O 的直径 ， AC 是 ⊙ O 的切线 ， 连接 OC 交 ⊙ O 于点 D ， 连接 BD ， ∠ C ＝ 40°. 则 ∠ ABD 的度数是 ( ) A ． 30° B ． 25° C ． 20° D ． 15° B 3 ． ( 2014 · 无锡 ) 如图 ， AB 是 ⊙ O 的直径 ， CD 是 ⊙ O 的切线 ， 切点为 D ， CD 与 AB 的延长线交于点 C ， ∠ A ＝ 30° ， 给出下面 3 个结论： ① AD ＝ CD ； ② BD ＝ BC ； ③ AB ＝ 2BC ， 其中正确结论的个数是 ( ) A ． 3 B ． 2 C ． 1 D ． 0 A 4 ． ( 2014 · 绍兴 ) 把球放在长方体纸盒内 ， 球的一部分露出盒外 ， 其主视图如图． ⊙ O 与矩形 ABCD 的边 BC ， AD 分别相切和相交 (E ， F 是交点 ) ， 已知 EF ＝ CD ＝ 8 ， 则 ⊙ O 的半径为 ． 5 判断直线与圆的位置关系 【 例 1 】 (1) 如图 ， ⊙ O 的半径为 4 cm ， OA ⊥ OB ， OC ⊥ AB 于 C ， OB ＝ 4 5 cm ， OA ＝ 2 5 cm ， 试说明 AB 是 ⊙ O 的切线． 解： ( 1 ) ∵ OA ⊥ OB ， ∴ AB ＝ OA 2 ＋ OB 2 ＝ （ 2 5 ） 2 ＋（ 4 5 ） 2 ＝ 10. 又 ∵ S △ AOB ＝ 1 2 AB·OC ＝ 1 2 OA·OB ， ∴ OC ＝ OA·OB AB ＝ 2 5 × 4 5 10 ＝ 4. 又 ∵⊙ O 的半径 为 4 ， ∴ AB 是 ⊙ O 的切线 (2) 如图 ， 已知在 △ OAB 中 ， OA ＝ OB ＝ 13 ， AB ＝ 24 ， ⊙ O 的半径长为 r ＝ 5. 判断直线 AB 与 ⊙ O 的位置关系 ， 并说明理由． 【 点评 】 　在判定直线与圆相切时 ， 若直线与圆的公共点已知 ， 证题方法是 “ 连半径 ， 证垂直 ” ；若直线与圆的公共点未知 ， 证题方法是 “ 作垂线 ， 证半径 ” ． 这两种情况可概括为一句话： “ 有交点连半径 ， 无交点作垂线 ” ． 1 ． ( 1 ) 如图 ， 以 O 为圆心的两个同心圆中 ， 大圆的弦 AB 切 小圆于点 C . 若 ∠ AOB ＝ 120 ° ， 则大圆半径 R 与小圆半径 r 之间满足 ( ) A ． R ＝ 3 r B ． R ＝ 3 r C ． R ＝ 2 r D ． R ＝ 2 2 r C (2) ( 2012 · 兰州 ) 如图 ， 两个同心圆 ， 大圆半径为 5 cm ， 小圆的半径为 3 cm ， 若大圆的弦 AB 与小圆相交 ， 则弦 AB 的取值范围是 ． 8 ＜ AB ≤ 10 圆的切线的性质 【 例 2 】 　 ( 2014 · 黄冈 ) 如图 ， 在 Rt △ ABC 中 ， ∠ ACB ＝ 90° ， 以 AC 为直径的 ⊙ O 与 AB 边交于点 D ， 过点 D 的切线 ， 交 BC 于点 E. (2) 若以点 O ， D ， E ， C 为顶点的四边形是正方形 ， 试判断 △ ABC 的形状 ， 并说明理由． 解：当以点 O ， D ， E ， C 为顶点的四边形是正方形时 ， 则 ∠ DEB ＝ 90° ， 又 ∵ DE ＝ BE ， ∴△ DEB 是等腰直角三角形 ， 则 ∠ B ＝ 45 ° ， ∴△ ABC 是等腰直角三角形 (1) 求证： EB ＝ EC ； 【 点评 】 　本题考查了切线的性质以及切线长定理、圆周角定理 ， 解题的关键是连接 CD 构造直角三角形． 2 ． ( 2014 · 凉山州 ) 如图 ， P 是 ⊙ O 外一点 ， 过点 P 引圆的切线 PC(C 为切点 ) 和割线 PAB ， 分别交 ⊙ O 于 A ， B ， 连接 AC ， BC. (1) 求证： ∠ PCA ＝ ∠ PBC ； (2) 利用 (1) 的结论 ， 已知 PA ＝ 3 ， PB ＝ 5 ， 求 PC 的长． 切线的判定与性质的综合运用 【 例 3 】 　 ( 2014 · 德州 ) 如图 ， ⊙ O 的直径 AB 为 10 cm ， 弦 BC 为 6 cm ， D ， E 分别是 ∠ ACB 的平分线与 ⊙ O ， AB 的交点 ， P 为 AB 延长线上一点 ， 且 PC ＝ PE. (1) 求 AC ， AD 的长； (2) 试判断直线 PC 与 ⊙ O 的位置关系 ， 并说明理由． 直线 PC 与 ⊙ O 相切 ， 理由：连接 OC ， ∵ OC ＝ OA ， ∴∠ CAO ＝ ∠ OCA ， ∵ PC ＝ PE ， ∴∠ PCE ＝ ∠ PEC ， ∵∠ PEC ＝ ∠ CAE ＋ ∠ ACE ， ∵ CD 平分 ∠ ACB ， ∴∠ ACE ＝ ∠ ECB ， ∴∠ PCB ＝ ∠ CAE ＝ ∠ ACO ， ∵∠ ACB ＝ 90 ° ， ∴∠ OCP ＝ ∠ OCB ＋ ∠ PCB ＝ ∠ ACO ＋ ∠ OCB ＝ ∠ ACB ＝ 90° ， OC ⊥ PC ， ∴ 直线 PC 与 ⊙ O 相切 【 点评 】 　本题主要考查了切线的判定和性质 ， 勾股定理和圆周角 ， 解题的关键是运用圆周角和角平分线及等腰三角形正确找出相等的角． 3 ． ( 2013 · 凉山州 ) 在同一平面直角坐标系中有 5 个点： A(1 ， 1) ， B( － 3 ， － 1) ， C( － 3 ， 1) ， D( － 2 ， － 2) ， E(0 ， － 3) ． (1) 画出 △ ABC 的外接圆 ⊙ P ， 并指出点 D 与 ⊙ P 的位置关系； (2) 若直线 l 经过点 D( － 2 ， － 2) ， E(0 ， － 3) ， 判断直线 l 与 ⊙ P 的位置关系． 连接 PE ， PD ， ∵直线 l 过点 D ( － 2 ， － 2 ) ， E ( 0 ， － 3 ) ， ∴ PE 2 ＝ 1 2 ＋ 3 2 ＝ 10 ， PD 2 ＝ 5 ， DE 2 ＝ 5. ∴PE 2 ＝ PD 2 ＋ DE 2 . ∴△ PDE 是直角三角形 ， 且 ∠ PDE ＝ 90°.∴PD⊥DE.∵ 点 D 在 ⊙ P 上 ， ∴直线 l 与 ⊙ P 相切 试题 已知：如图 ， P 是 ⊙ O 外一点 ， PA 切 ⊙ O 于点 A ， AB 是 ⊙ O 的直径 ， BC ∥ OP 交 ⊙ O 于点 C . ( 1 ) 判 断直线 PC 与 ⊙ O 的位置关系 ， 并证明你的结论； ( 2 ) 若 BC ＝ 2 ， sin 1 2 ∠ APC ＝ 1 3 ， 求 PC 的长及点 C 到 PA 的 距离 ． 审题视角 ( 1 ) 直线 PC 与 ⊙ O 交于点 C ， 可以初步判定直线与圆相切 或相交； ( 2 ) PA 切 ⊙ O 于点 A ， 根据切线的性质 ， 可知 ∠ PAO ＝ 90 ° ， 连接 CO ， 能证得 ∠ PCO ＝ ∠ PAO ＝ 90 ° ， PC 与 ⊙ O 相切； 而后由 PC 是切线解得 PC 长 ． 规范解题 解： (1) 直线 PC 与 ⊙ O 相切． 证明：连接 OC ， ∵ BC ∥ OP ， ∴∠ 1 ＝ ∠ 2 ， ∠ 3 ＝ ∠ 4. ∵ OB ＝ OC ， ∴∠ 1 ＝ ∠ 3 ， ∴∠ 2 ＝ ∠ 4. 又 ∵ OC ＝ OA ， OP ＝ OP ， ∴△ POC ≌△ POA ， ∴∠ PCO ＝ ∠ PAO . ∵ PA 切 ⊙ O 于点 A ， ∴∠ PAO ＝ 90 ° ， ∴∠ PCO ＝ 90 ° ， ∴ PC 与 ⊙ O 相切． ( 2 ) ∵△ POC ≌△ POA ， ∴∠ 5 ＝ ∠ 6 ＝ 1 2 ∠ APC ， ∴ sin ∠ 5 ＝ sin 1 2 ∠ APC ＝ 1 3 . ∵∠ PCO ＝ 90 ° ， ∴∠ 2 ＋ ∠ 5 ＝ 90 ° ， ∴ cos ∠ 2 ＝ sin ∠ 5 ＝ 1 3 . ∵∠ 3 ＝ ∠ 1 ＝ ∠ 2 ， ∴ cos ∠ 3 ＝ 1 3 . 连接 AC ， ∵ AB 是 ⊙ O 的直径 ， ∴∠ ACB ＝ 90 ° ， ∴ AB ＝ BC cos ∠ 3 ＝ 2 1 3 ＝ 6 ， ∴ OA ＝ OB ＝ OC ＝ 3 ， AC ＝ AB 2 － BC 2 ＝ 4 2 ， ∴ 在 Rt △ POC 中 ， OP ＝ OC s in ∠ 5 ＝ 9 ， ∴ PC ＝ OP 2 － OC 2 ＝ 6 2 . 过点 C 作 CD ⊥ PA 于 D ， ∵∠ ACB ＝ ∠ PAO ＝ 90 ° ， ∴∠ 3 ＋ ∠ 7 ＝ 90 ° ， ∠ 7 ＋ ∠ 8 ＝ 90 ° ， ∴∠ 3 ＝ ∠ 8 ， ∴ cos ∠ 8 ＝ cos ∠ 3 ＝ 1 3 . 在 Rt △ CAD 中 ， AD ＝ AC · cos ∠ 8 ＝ 4 2 × 1 3 ＝ 4 3 2 . ∴ CD ＝ AC 2 － AD 2 ＝ 16 3 ， 即点 C 到 PA 的 距离为 16 3 . 答题思路 第一步：探索可能的结论 ， 假设符合要求的结论存在； 第二步：从条件出发 ( 即假设 ) 求解； 第三步：确定符合要求的结论存在或不存在； 第四步：给出明确结果； 第五步：反思回顾 ， 查看关键点 ， 易错点及答题规范． 试题 在 Rt △ ABC 中 ， ∠ C ＝ 90 ° ， AC ＝ 3 ， BC ＝ 4 ， 若以 C 为圆心 ， R 为半径的圆与斜边 AB 只有一个公共点 ， 求 R 的值． 错解 解： ∵⊙ C 与 AB 相切 ， 此时 AB ＝ 3 2 ＋ 4 2 ＝ 5 ， S △ ABC ＝ 1 2 AB · CD ＝ 1 2 AC · BC ∴ CD ＝ AC · BC AB ＝ 3 × 4 5 ＝ 12 5 ， ∴ 圆与 AB 相切时 ， 即 R ＝ CD ＝ 12 5 . 剖析 　当 ⊙ C 与 AB 相切时 ， 只有一个交点 ， 同时要注意 AB 是线段 ， 当圆的半径 R 在一定范围内时 ， 斜边 AB 与 ⊙ C 相交且只有一个公共点． 正解 解：当 ⊙ O 与 AB 相切时 ， AB ＝ 3 2 ＋ 4 2 ＝ 5 ， ∵ S △ ABC ＝ 1 2 AB · CD ＝ 1 2 AC · BC ， ∴ CD ＝ AC · BC AB ＝ 3 × 4 5 ＝ 12 5 ； 当 ⊙ C 与斜边 AB 相交时 ， 点 A 在圆内部 ， 点 B 在圆上或圆外 时 ， 此时 AC ＜ R ≤ BC ， 即 3 ＜ R ≤ 4. 故答案为： 3 ＜ R ≤ 4 或 R ＝ 12 5 .