2013中考数学复习几何探索题的特点独创

2013中考数学复习几何探索题的特点独创

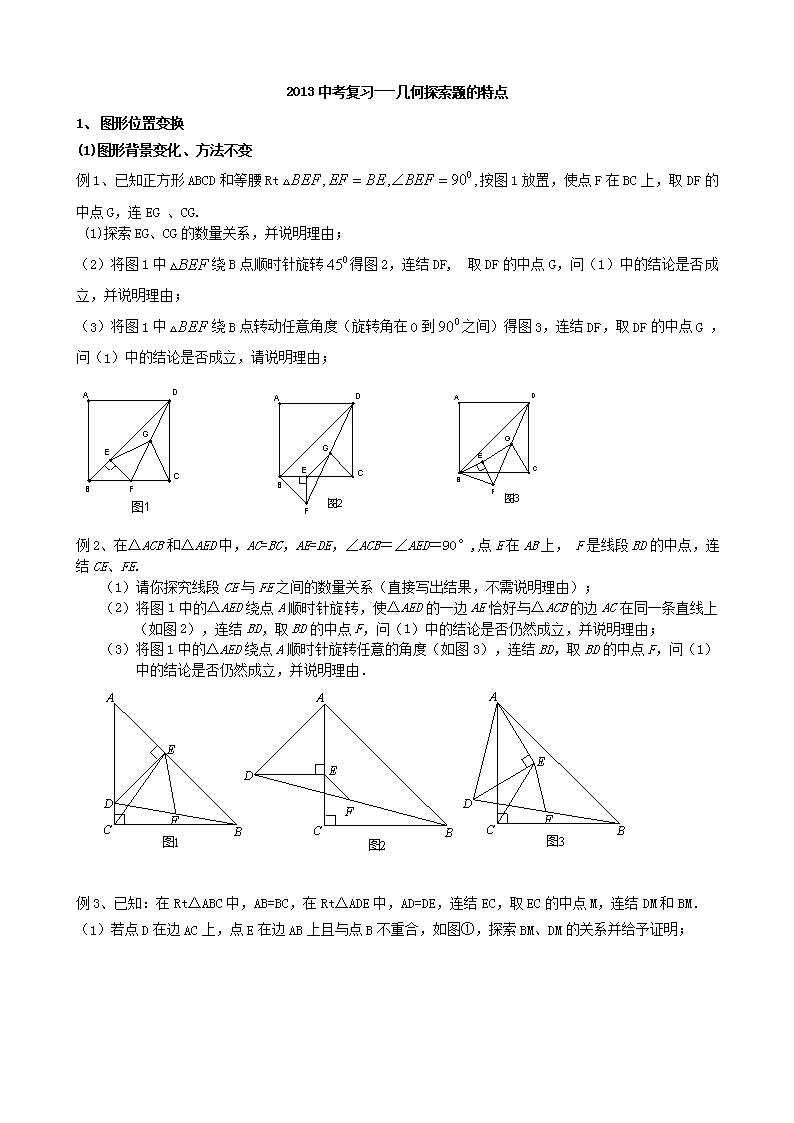
‎2013中考复习---几何探索题的特点 1、 图形位置变换 ‎(1)图形背景变化、方法不变 例1、已知正方形ABCD和等腰Rt按图1放置，使点F在BC上，取DF的中点G，连EG 、CG.‎ ‎(1)探索EG、CG的数量关系，并说明理由；‎ ‎（2）将图1中绕B点顺时针旋转得图2，连结DF, 取DF的中点G，问（1）中的结论是否成立，并说明理由；‎ ‎（3）将图1中绕B点转动任意角度（旋转角在0到之间）得图3，连结DF，取DF的中点G ，问（1）中的结论是否成立，请说明理由；‎ 例2、在△ACB和△AED中，AC=BC，AE=DE，∠ACB＝∠AED＝90°,点E在AB上， F是线段BD的中点，连结CE、FE.‎ ‎（1）请你探究线段CE与FE之间的数量关系（直接写出结果，不需说明理由）；‎ ‎（2）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连结BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由；‎ ‎ （3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3），连结BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由．‎ ‎ ‎ 例3、已知：在Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连结EC，取EC的中点M，连结DM和BM．‎ ‎（1）若点D在边AC上，点E在边AB上且与点B不重合，如图①，探索BM、DM的关系并给予证明； ‎ 图②‎ 图①‎ ‎（2）如果将图①中的△ADE绕点A逆时针旋转小于45°的角，如图②，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明．‎ 例4、在图中，四边形ABCD和CGEF都是正方形，M是AE的中点． ‎ ‎（1）如图1，点G在BC延长线上，求证：DM=MF； （2）在图1的基础上，将正方形CGEF绕点C顺时针旋转到图2位置，此时点E在BC延长线上．求证：DM=MF； （3）在图2的基础上，将正方形CGEF绕点C在任一旋转一个角度到如图3位置，此时DM和MF还相等吗？（说明理由）‎ ‎（2）图形位置变，结论类似 例5、如图，C为BD上一点，分别以BC和CD为边向同侧作等边三角形ABC和ECD，AD和BE相交于点M． ‎ ‎ ‎ 探究线段BE和AD的数量关系和位置关系．‎ 本题可以作如下变换：‎ ‎（1）绕点C变化时，探究线段BE和AD的数量关系和位置关系．‎ ‎（2）把和△ECD改为等腰直角三角形，探究线段BE和AD的数量关系。‎ ‎（3）把和△ECD改为顶角为α等腰三角形，探究线段BE和AD的数量关系。‎ 1、 图形形状改变 （1） 三角形费马点到三顶点距离和最小变换为正方形对角线上一点到三顶点距离和最小 E A D B C N M 例题1、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.‎ ‎⑴ 求证：△AMB≌△ENB；‎ ‎⑵ ①当M点在何处时，AM＋CM的值最小；‎ ‎②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；‎ ‎⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.‎ （2） 正三角形—正四边形—正六边形 F E A D B C N M 例如：F E A D B C N M 正三角形内一点P，PA=3，PB=4，PC=5，求∠APB和AB---正方形内一点P求∠APB和AB 例题2、阅读下列材料：‎ 问题：如图1，在正方形ABCD内有一点P，PA=，PB=，PC=1，求∠BPC的度数．‎ 小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．‎ 请你参考小明同学的思路，解决下列问题：‎ ‎(1) 图2中∠BPC的度数为 ；‎ ‎(2) 如图3，若在正六边形ABCDEF内有一点P，且PA=，PB=4，PC=2，则∠BPC的度数为 ，正六边形ABCDEF的边长为 ．‎ ‎ ‎ ‎ 图1 ‎ 例3、正三角形变换为正方形ABCD中，E是BC上一点，AE⊥EG交∠DCH的平分线于G，求证：AE=EG，进一步变换为正六边形。‎ 例4、已知:在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD当∠ACB变化,且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数.‎ 改编：以AB为边作正方形ABDE；以AB为边作正六边形方形ABDEFG；‎ 如：已知：，，以AB为一边作正方形ABCD，使P、D两点落在直线AB ‎ 的两侧.‎ ‎（1）如图，当∠APB=45°时，求AB及PD的长；‎ ‎（2）当∠APB变化，且其它条件不变时，求PD 的 ‎ 最大值，及相应∠APB的大小.‎ 例5、已知如图，△ABC和△DCE都是等边三角形，若△ABC的边长为1，则△BAE的面积是 .‎ 四边形ABCD和四边形BEFG都是正方形，若正方形ABCD的边长为4，则△FAC的面积是 .……‎ 如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形，正多边形ABCDE …的边长是‎2a，则△KCA的面积是 .（结果用含有a、n的代数式表示）‎ 例6、如图24－1，正方形ABCD和正方形QMNP， M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．‎ ‎（1）猜想：ME 与MF的数量关系____________________‎ ‎（2）如图24－2，若将原题中的“正方形”改为“菱形”，且∠M =∠B，其它条件不变，探索线段ME与线段MF的数量关系，并加以证明．‎ ‎（3）如图24－3，若将原题中的“正方形”改为“矩形”，且AB:BC=1:2，其它条件不变，探索线段ME与线段MF的数量关系，并说明理由．‎ ‎（4）如图24－4，若将原题中的“正方形”改为平行四边形，且∠M =∠B ，AB:BC = m，其它条件不变，则ME：MF=_______________‎ 例7、如图，点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且BE=CD，DB的延长线交AE于点F，则图1中∠AFB的度数为 ；若将条件“正三角形、正四边形、正五边形”改为“正n边形”，其他条件不变，则∠AFB 的度数为 ．（用n的代数式表示，其中，≥3，且为整数）‎ ‎ ‎ 例8、（2009宣武二模24）(1)已知： 是⊙的内接正三角形，点为弧BC上一动点，求证：‎ ‎(2) 如图2，四边形是⊙的内接正方形，点为弧BC上一动点，求证: ‎ ‎(3) 如图3，六边形是⊙的内接正六边形，点为弧BC上一动点，请探究三者之间有何数量关系，并给予证明. ‎ 1、 图形边角一般化 例1、已知:在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD. 探究下列问题:‎ ‎（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD= ；‎ ‎（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD= ；‎ ‎（3）如图3，当∠ACB变化,且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数.‎ ‎ ‎ 例2、在Rt△ABC中，∠ACB=90，AC=BC，CD⊥AB于点D，点E为AC边上一点，联结BE交CD于点F，过点E作EG⊥BE交AB于点G，‎ （1） 如图1，当点E为AC中点时，线段EF与EG的数量关系是 ；‎ （2） 如图2，当，探究线段EF与EG的数量关系并且证明；‎ （3） 如图3，当，线段EF与EG的数量关系是 ．‎ 图1 图2 图3‎ 例3、在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流.‎ 原问题：如图1，已知△ABC, ∠ACB=90° , ∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE, 且DA=DB, EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F. 探究线段DF与EF的数量关系.‎ 小慧同学的思路是：过点D作DG⊥AB于G,构造全等三角形，通过推理使问 题得解.‎ 小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.‎ 小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况.‎ 请你参考小慧同学的思路，探究并解决这三位同学提出的问题：‎ ‎（1）写出原问题中DF与EF的数量关系；‎ ‎（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在 ‎（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；‎ ‎（3）如图3，若∠ADB=∠BEC=2∠ABC, 原问题中的其他条件不变，你在（1）中 得到的结论是否发生变化？请写出你的猜想并加以证明.‎ ‎ ‎ 图1 图2 图3‎ 例4、如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连结EF，求证DE+BF=EF．‎ 感悟解题方法，并完成下列填空：‎ 将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：‎ AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,‎ ‎∴∠ABG+∠ABF=90°+90°=180°，‎ 因此，点G，B，F在同一条直线上．‎ ‎∵∠EAF=45° ， ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．‎ ‎∵∠1=∠2， ∴∠1+∠3=45°．‎ 即∠GAF=∠_________．‎ 又AG=AE，AF=AF,‎ ‎∴△GAF≌_______．‎ ‎∴_________=EF，故DE+BF=EF． ‎ ‎⑵方法迁移：‎ 如图②，将沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．‎ ‎⑶问题拓展：‎ 如图③，在四边形ABCD中，AB=AD，E，F分别为DC,BC上的点，满足,试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．‎ 例5、（09怀柔一模25）如图1，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：‎ ‎（1）如果AB=AC，∠BAC=90º．‎ 图1‎ 图2‎ 图3‎ ①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD之间的位置关系为 ，数量关系为 ．‎ ②当点D在线段BC的延长线上时，如图3，①中的 结论是否仍然成立，为什么？‎