人教版八年级数学上册期末测试题及答案1

人教版八年级数学上册期末测试题及答案1

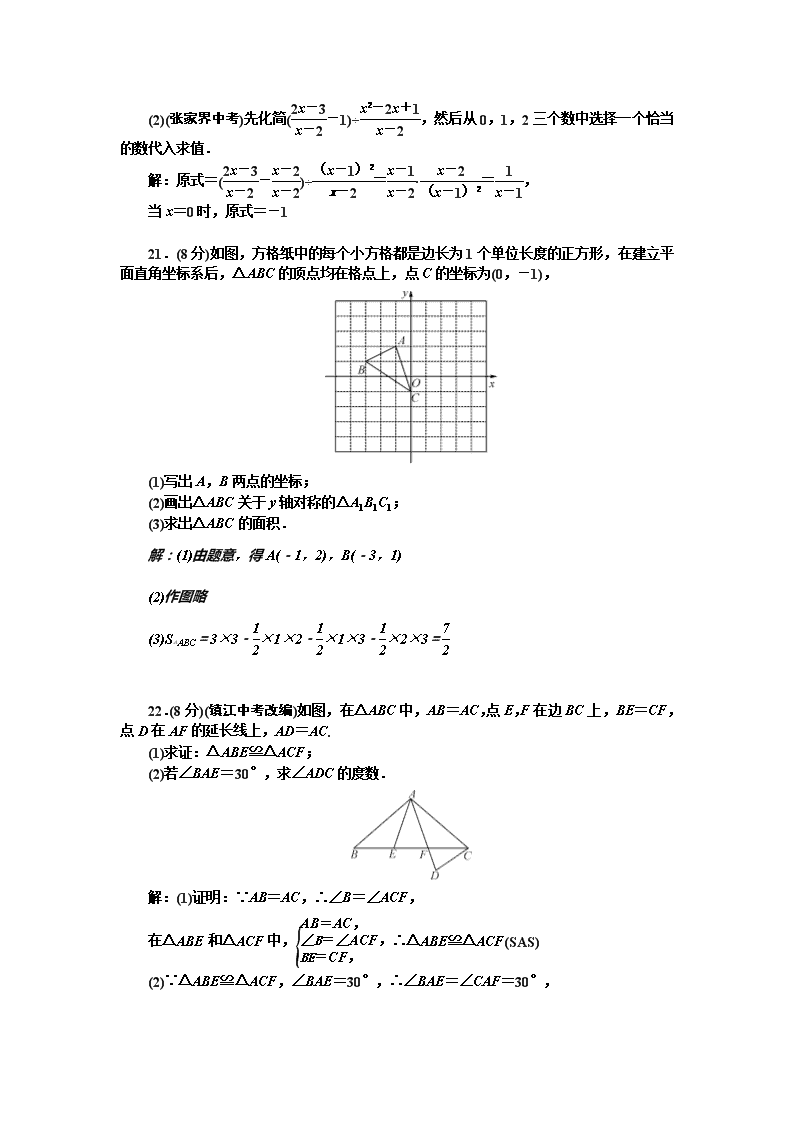
期末检测（一）‎ 得分________　卷后分________　评价________‎ ‎　　　　　　　　　　 　　　　　　　　　　 　　　　　　　　　　‎ 一、选择题(每小题3分，共30分)‎ ‎1．誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文文字明显不是轴对称图形的是(C)‎ ‎2．要使分式有意义，则x的取值范围为(D)‎ A．x>－2 B．x<－2 C．x≠0 D．x≠－2‎ ‎3. (宿迁中考)下列运算正确的是(D)‎ A．a2＋a3＝a5 B．(a2)3＝a5 C．a6÷a3＝a2 D．(ab2)3＝a3b6‎ ‎4．如图，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是(C)‎ A．AB＝DE B．AC＝DF C．∠A＝∠D D．BF＝EC 　　　　　　 ‎5．下列运算中，错误的有(D)‎ ‎①(2x＋y)2＝4x2＋y2，②(a－3b)2＝a2－9b2，③(－x－y)2＝x2－2xy＋y2，④(x－)2＝x2－2x＋.‎ A．1个 B．2个 C．3个 D．4个 ‎6．(张家界中考)如图，在△ABC中，∠C＝90°，AC＝8，DC＝AD，BD平分∠ABC，则点D到AB的距离等于(C)‎ A．4 B．3 C．2 D．1‎ ‎7．(荆州中考)已知关于x的分式方程－2＝的解为正数，则k的取值范围为(B)‎ A．－2＜k＜0 B．k＞－2且k≠－1 C．k＞－2 D．k＜2且k≠1‎ ‎8．如图，在△ABC中，AB＝AC，点D，E分别在边BC 和AC上，若AD＝AE，则下列结论错误的是(D)‎ A．∠ADB＝∠ACB＋∠CAD B．∠ADE＝∠AED C．∠CDE＝∠BAD D．∠AED＝2∠ECD ‎9．如图，若AB＝AC，BG＝BH，AK＝KG，则∠BAC的度数为(C)‎ A．30° B．32° C．36° D．40°‎ ‎10．如图，在△ABC中，AB＞AC，延长CA至点G，边BC的垂直平分线DF与∠BAG的平分线交于点D，与AB交于点H，垂足为F，DE⊥AB于点E.下列结论：①BH＝FC；②∠GAD＝(∠B＋∠HCB)；③BE－AC＝AE；④∠B＝∠ADE.其中说法正确的有(A)‎ A．1个 B．2个 C．3个 D．4个 二、填空题(每小题3分，共24分)‎ ‎11．(黄冈中考)分解因式：3x2－27y2＝3(x＋3y)(x－3y)．‎ ‎12．(临沂中考)在平面直角坐标系中，点P(4，2)关于直线x＝1的对称点的坐标是(－2，2)．‎ ‎13．如图，过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的平分线相交于点P，且∠ABP＝60°，则∠APB＝66度．‎ ‎14．多项式x2＋mx＋25恰好是另一个多项式的平方，则m＝__±10__．‎ ‎15．(内江中考)若＋＝2，则分式的值为－4．‎ ‎16．如图，△ABE，△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1∶∠2∶∠3＝7∶2∶1，则∠α的度数为108°．‎ ‎17．使得关于x的分式方程－＝1的解为负整数，且使得关于x的不等式组有且仅有5个整数解的所有k的和为__12.5__．‎ ‎18．如图，在△ABC中，∠C＝90°，∠A＝30°，BC＝3，P是AB上的一动点，PE⊥AC于点E，沿PE将∠A折叠，点A的对应点为D，若△BPD是直角三角形，则PA的长为__2或4__．‎ 三、解答题(共66分)‎ ‎19．(8分)(1)(黔东南州中考)计算：|－|＋(－1)2 019＋2－1－(π－3)0；‎ 解：原式＝－1＋－1＝－1‎ ‎(2)解方程：1－＝.‎ 解：去分母，得2x＋2－x＋3＝6x，‎ 解得x＝1，‎ 经检验x＝1是分式方程的解 ‎20．(8分)先化简，再求值：‎ ‎(1)(x＋1)(x－1)＋x(3－x)，其中x＝2；‎ 解：原式＝x2－1＋3x－x2＝3x－1.当x＝2时，原式＝3×2－1＝5‎ ‎(2)(张家界中考)先化简(－1)÷，然后从0，1，2三个数中选择一个恰当的数代入求值．‎ 解：原式＝(－)÷＝·＝，‎ 当x＝0时，原式＝－1‎ ‎21．(8分)如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为(0，－1)，‎ ‎(1)写出A，B两点的坐标；‎ ‎(2)画出△ABC关于y轴对称的△A1B1C1；‎ ‎(3)求出△ABC的面积．‎ 解：(1)由题意，得A(－1，2)，B(－3，1)‎ ‎(2)作图略 ‎(3)S△ABC＝3×3－×1×2－×1×3－×2×3＝ ‎22．(8分)(镇江中考改编)如图，在△ABC中，AB＝AC，点E，F在边BC上，BE＝CF，点D在AF的延长线上，AD＝AC.‎ ‎(1)求证：△ABE≌△ACF；‎ ‎(2)若∠BAE＝30°，求∠ADC的度数．‎ 解：(1)证明：∵AB＝AC，∴∠B＝∠ACF，‎ 在△ABE和△ACF中，∴△ABE≌△ACF(SAS)‎ ‎(2)∵△ABE≌△ACF，∠BAE＝30°，∴∠BAE＝∠CAF＝30°，‎ ‎∵AD＝AC，∴∠ADC＝∠ACD，∴∠ADC＝＝75°‎ ‎23．(10分)(遂宁中考)仙桃是某地的特色时令水果．仙桃一上市，水果店的老板用2‎ ‎ 400元购进一批仙桃，很快售完；老板又用3 700元购进第二批仙桃，所购件数是第一批的倍，但进价比第一批每件多了5元．‎ ‎(1)第一批仙桃每件进价是多少元？‎ ‎(2)老板以每件225元的价格销售第二批仙桃，售出80%后，为了尽快售完，剩下的决定打折促销．要使得第二批仙桃的销售利润不少于440元，剩余的仙桃每件售价至多能打几折？(利润＝售价－进价)‎ 解：(1)设第一批仙桃每件进价是x元，则×＝，解得x＝180.‎ 经检验，x＝180是原方程的解．答：第一批仙桃每件进价为180元 ‎(2)设剩余的仙桃每件售价打y折，则×225×80%＋×225×(1－80%)×0.1y－3 700≥440，解得y≥6.‎ 答：剩余的仙桃每件售价至多能打6折 ‎24．(11分)如图，等边△ABC的边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F.‎ ‎(1)若AD＝2，求AF的长；‎ ‎(2)当AD取何值时，DE＝EF?‎ 解：(1)∵△ABC为等边三角形，∴AB＝BC＝AC＝8，∠B＝60°.∵AB＝8，AD＝2，∴BD＝AB－AD＝6.在Rt△BDE中，∠BDE＝90°－∠B＝30°，∴BE＝BD＝3，∴CE＝BC－BE＝5.在Rt△CFE中，∠CEF＝90°－∠C＝30°，∴CF＝CE＝，∴AF＝AC－CF＝ ‎(2)在△BDE和△CEF中，∵∠BED＝∠CFE＝90°，∠B＝∠C，DE＝EF，∴△BDE≌△CEF(AAS).∴BE＝CF.由(1)可知，BD＝2BE，CF＝EC，∴BE＝CF＝EC.∴BE＝BC＝，∴BD＝2BE＝，∴AD＝AB－BD＝.因此，当AD＝时，DE＝EF ‎25．(13分)如图①，点C在线段AB上(点C不与A，B重合)，分别以AC，BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE，BD交于点P.‎ ‎(1)观察猜想：‎ ‎①AE与BD的数量关系为__AE＝BD__；‎ ‎②∠APD的度数为__60°__；‎ ‎(2)数学思考：‎ 如图②，当点C在线段AB外时，(1)中的结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；‎ ‎(3)拓展应用：‎ 如图③，点E为四边形ABCD内一点，且满足∠AED＝∠BEC＝90°，AE＝DE，BE＝CE.对角线AC，BD交于点P，AC＝10，则四边形ABCD的面积为__50__．‎ 解：(2)上述结论成立．∵△ACD，△BCE均为等边三角形，∴DC＝AC，BC＝EC，∠DCA＝∠BCE＝60°，∴∠DCA＋∠ACB＝∠ACB＋∠BCE.即∠DCB＝∠ACE.在△DCB和△ACE中，∴△DCB≌△ACE(SAS)，∴DB＝AE，∠CDB＝∠CAE.设BD与AC交于点O，易知∠DOC＝∠AOP(对顶角相等)，∴∠CDB＋∠DCA＝∠CAE＋∠DPA，‎ ‎∴∠DCA＝∠DPA＝60°，即∠APD＝60°‎ ‎(3)可证△DEB≌△AEC(SAS)，∴DB＝AC＝10，∠EDB＝∠EAC.设BD与AE交于点O，易知∠DOE＝∠AOP，∴∠EDB＋∠DEA＝∠EAC＋∠DPA，∴∠DPA＝∠DEA＝90°，即BD⊥AC，∴S四边形ACBD＝×BD×AC＝×10×10＝50‎