2020八年级数学上册 第11章 三角形 11.3.2 多边形的内角和

2020八年级数学上册 第11章 三角形 11.3.2 多边形的内角和

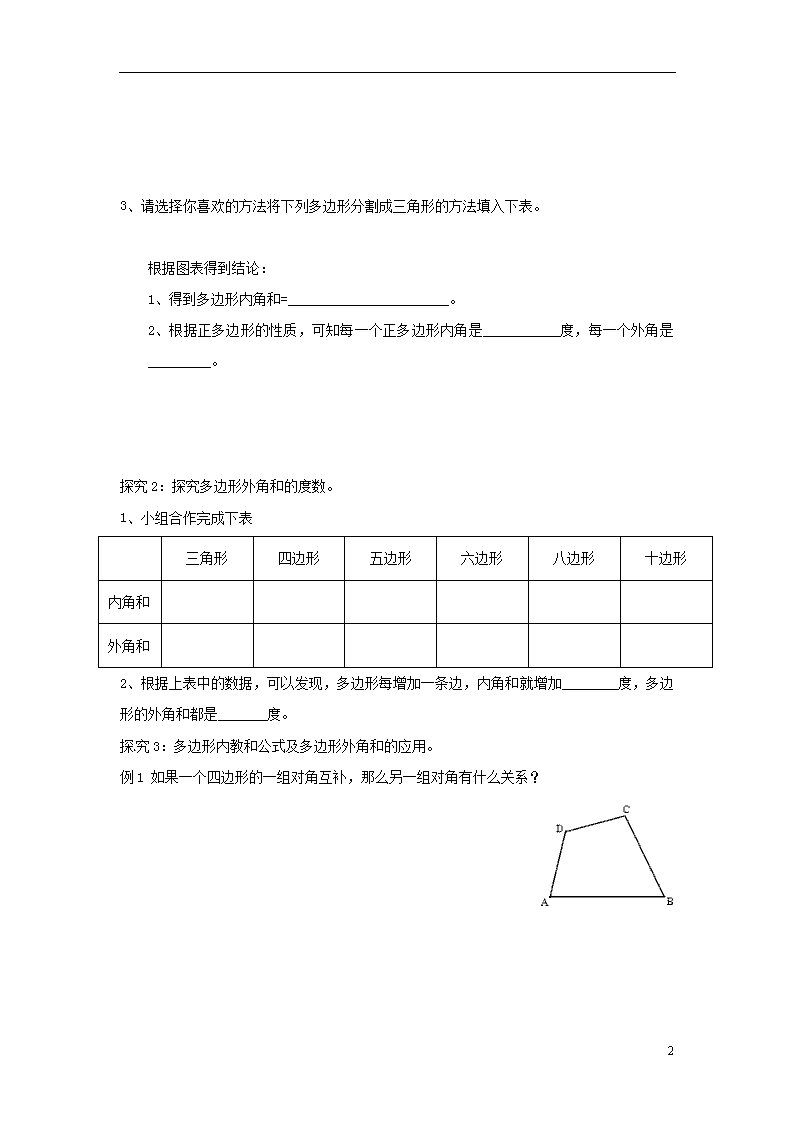
课题：‎11.3.2‎ 多边形的内角和 ‎【学习目标】‎ ‎1、使学生了解多边形内角、外角的概念；‎ ‎2、能通过不同方法探索多边形的内角和与外角和公式，并会应用它们进行有关计算。‎ ‎【学习重点】‎ ‎1、多边形的内角和公式；‎ ‎2、多边形的外角和公式。‎ ‎【学习难点】‎ 如何把多边形转化为三角形，用分割多边形法推导多边形的内角和。‎ ‎【学习过程】‎ ‎※ 知识链接 （1） 三角形内角和等于_______度，四边形内角和等于_______度。‎ ‎（2）你如何得到四边形内角和这个结论的？‎ ‎※ 合作与探究 一、自主学习 ‎1、阅读教材第21至第23页，用红笔对有关概念进行勾画并完成下列问题。‎ ‎2、找出自己的疑惑和要讨论的问题，准备在课堂上讨论质疑 二、合作探究 探究1：探究多边形内角和的度数。‎ ‎1、如图，请你利用分割的方法探索六边形的内角和是多少度？‎ ‎2、你可以用多少种方法分割六边形探究六边形内角和的度数？请在下图中画出来。‎ 4‎ ‎3、请选择你喜欢的方法将下列多边形分割成三角形的方法填入下表。‎ 多边形的边数 图形 分割出三角形的个数 多边形的内角和 ‎4‎ ‎5‎ ‎6‎ ‎…‎ ‎…‎ ‎…‎ ‎…‎ n 根据图表得到结论：‎ ‎1、得到多边形内角和=_______________________。‎ ‎2、根据正多边形的性质，可知每一个正多边形内角是___________度，每一个外角是_________。‎ 探究2：探究多边形外角和的度数。‎ ‎1、小组合作完成下表 三角形 四边形 五边形 六边形 八边形 十边形 内角和 外角和 ‎2、根据上表中的数据，可以发现，多边形每增加一条边，内角和就增加________度，多边形的外角和都是_______度。‎ 探究3：多边形内教和公式及多边形外角和的应用。‎ 例1 如果一个四边形的一组对角互补，那么另一组对角有什么关系？‎ 4‎ ‎※ 随堂检测 1、 判断题 （1） 当多边形的边数增加时，它的内角和的度数也增加 （ ）‎ （2） 当多边形的边数增加时，它的外角和的度数也增加 （ ）‎ （3） 三角形的外角和与八边形的外角和相等 （ ）‎ （4） 从n边形一个顶点出发，可以引出（n -2）条对角线，得到（n-2）个三角形（ ）‎ ‎2、填空题 ‎（1）一个多边形的内角和是4320º，则它的边数为___________ 。‎ ‎（2）五边形内角和为_________，它的对角线共有_______条。‎ ‎（3）一个多边形的每一个外角都等于30º，则这个多边形为______边形。‎ ‎（4）一个多边形的每一个内角都等于135º，则这个多边形为_______边形。‎ ‎（5）如果一个多边形的边数增加一条，那么这个多边形的内角和就增加________度，外角和就增加________度。‎ ‎3、选择题 ‎（1）多边形的每一个外角与它相邻内角的关系是（ ）‎ A、互为余角 B、互为邻补角 C、两个角相等 D、外角大于内角 ‎（2）多边形的内角和为它的外角和的4倍，这个多边形是（ ）‎ A、八边形 B、九边形 C、十边形 D、十一边形 ‎※ 拓展提高 1、 如图1，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中 ‎ ∠ +∠的度数是（ ）‎ A、180º B、220º C、240º D、300º 2、 如图2，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1+∠2之间的数量关系是（ ）‎ 4‎ A、 ‎∠A=∠1+∠2 B、2∠A=∠1+∠2 ‎ C、3∠A=2∠1+∠2 D、3∠A=2（∠1+∠2）‎ 教（学）后反思：_____________________________________________________________________‎ ‎_____________________________________________________________________ （实际使用课时 ______节）‎ 4‎