角平分线教学设计

角平分线教学设计

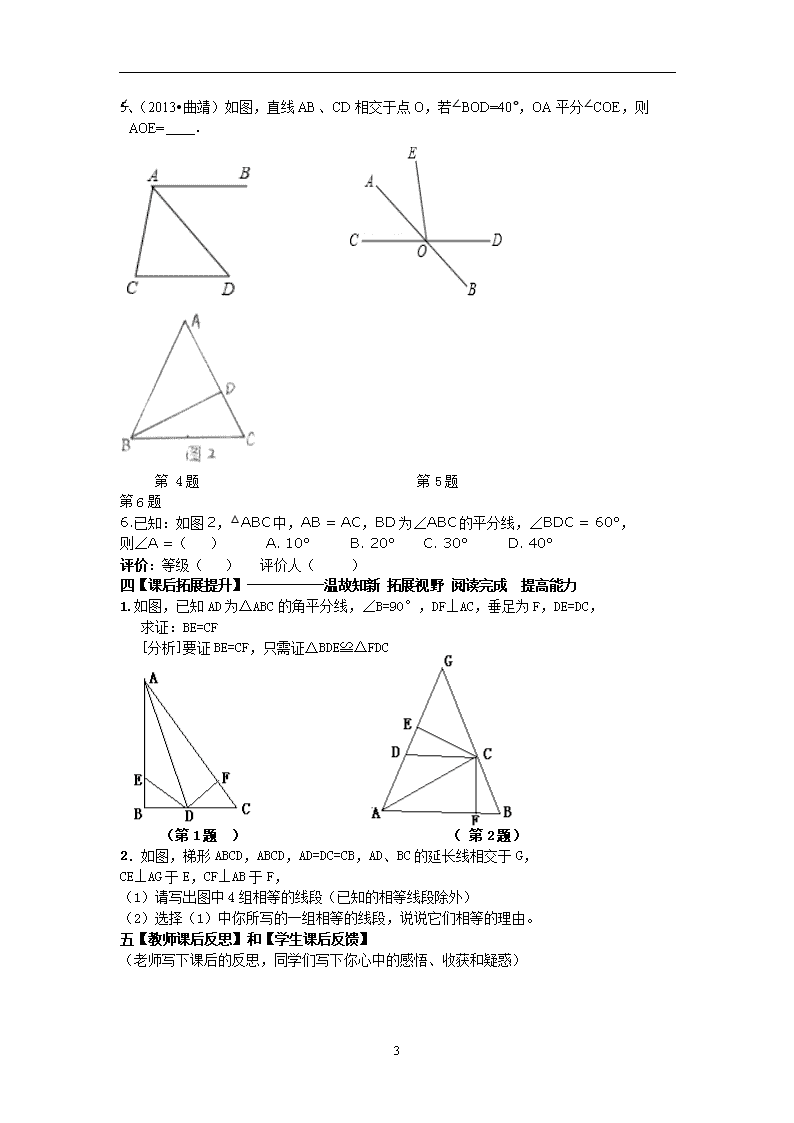
‎1.4、角平分线教学设计 ‎【三维目标】知识与能力1．要求学生掌握角平分线的性质定理及其逆定理——判定定理，会用这两个定理解决一些简单问题。‎ ‎2．理解角平分线的性质定理和判定定理的证明。‎ ‎3．能够作已知角的角平分线，并会熟练地写出已知、求作和作法，可以说明为什么所作的直线是角平分线。‎ 过程与方法:通过探索与证明，进一步发展推理意识及能力；‎ 情感态度价值观:证明是严密推理的方法，并培养自身的逆向思维能力 ‎【教学重点】角平分线性质定理及其逆定理。‎ ‎【教学难点】掌握角平分线性质定理及其逆定理并进行证明。‎ ‎【使用说明及学法指导】：1.学生预习本节内容完成导学案. 2. 探索讨论、证明、归纳总结。‎ ‎【导学流程】‎ 一【课前自主预习】-------建立自信 克服畏惧 独立预习 课前完成。‎ ‎1.回顾角平分线的定义。‎ ‎2.要平分一个角，可以用什么方法？‎ ‎3.角平分线的性质：角平分线上的点到角两边的距离相等。这一命题的条件和结论分别是什么？它的逆命题是                                                                                    .‎ 点拨：评价：等级（ ） 评价人（ ）‎ 二【课堂合作探究】---------小组学习 加强交流 积极发言 勇于展示。‎ ‎（一）、探究角平分线性质定理（学生根据命题写出已知和求证、证明要规范严谨，要做到说理有据。）‎ O D A P E B C 已知：OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E。‎ 求证：PD=PE ‎ ‎ ‎1.以黑板上学生的板演为样本，要求学生严格写出已知和求证，讲解其证明。‎ ‎2.对学生不规范的书写和表达予以纠正，同时理顺学生的证明。‎ 定理：角平分线上的点到这个角两边的距离相等。‎ ‎（二）、探究角平分线判定定理。‎ O D A P E B C 已知：如图，点P在射线OC上，PD⊥OA，PE⊥OB，垂足分别为D，E，且PD=PE。‎ 求证：OC是∠AOB的角平分线 3‎ 定理：在一个角的内部，且到角的两边距离相等的点，在这个角的平分线上。‎ ‎1.以黑板上学生的板演为样本，学生讲解其证明。对学生不规范的书写和表达予以纠正，同时理顺学生的证明思路。并注重纠错。‎ ‎2.引导学生回忆有关线段垂直平分线的性质定理和判定定理：它们有什么关系?在这里，角平分线的性质定理和要证明的命题是不是也有这个关系? （类比的方法）‎ ‎（三）、用直尺和圆规作角的平分线。‎ 已知：∠AOB 求作：射线OC，使∠AOC=∠BOC。‎ ‎1．让学生口述、演示和自己的实际操作，自己写出已知和求作，说出作法。锻炼学生的数学表达能力。‎ ‎2．选取学生有代表性的错误或不规范的地方予以修正，然后让学生仔细看书上写的作法，体会数学语言的精炼和严谨。‎ ‎3．让学生思考：这样作角平分线的理由是什么?为什么作出的射线就是角的平分线?让学生对这个作法有一个很好的理解，而不只是机械的模仿。‎ 评价：等级（ ） 评价人（ ）‎ 三【课堂能力训练】-----------仔细读题 积极思考 认真完成 准确评价 ‎1.工人师傅常用角尺平分一个任意角．做法如下：如图所示，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C作射线OC.由做法得△MOC≌△NOC的依据是(　　)A．AAS　　　B． SAS　　　C．ASA　　　D．SSS ‎2.如图所示，在△ABC中，AB＝AC，CD平分∠ACB，∠A＝36°，则∠BDC的度________‎ ‎ ‎ ‎ （第1题） （第2题） （第3题）‎ 中考链接：3（2013成都市）如图，，若AB∥CD，CB平分，则__度。‎ ‎4、（2013•雅安）如图，AB∥CD，AD平分∠BAC，且∠C=80°，则∠D的度数为（　　）‎ ‎　‎ A．‎ ‎50°‎ B．‎ ‎60°‎ C．‎ ‎70°‎ D．‎ ‎100°‎ 3‎ ‎5、（2013•曲靖）如图，直线AB、CD相交于点O，若∠BOD=40°，OA平分∠COE，则∠AOE=　　．‎ ‎ ‎ 第 4题 第5题 第6题 ‎6.已知：如图2，△ABC中，AB = AC，BD为∠ABC的平分线，∠BDC = 60°，则∠A =（    ） A. 10°        B. 20° C. 30°        D. 40°‎ 评价：等级（ ） 评价人（ ）‎ 四【课后拓展提升】-----------温故知新 拓展视野 阅读完成 提高能力 ‎1.如图，已知AD为△ABC的角平分线，∠B=90°，DF⊥AC，垂足为F，DE=DC，‎ 求证：BE=CF ‎ [分析]要证BE=CF，只需证△BDE≌△FDC ‎ ‎ ‎（第1题 ） （ 第2题）‎ ‎2．如图，梯形ABCD，ABCD，AD=DC=CB，AD、BC的延长线相交于G，‎ CE⊥AG于E，CF⊥AB于F，‎ ‎（1）请写出图中4组相等的线段（已知的相等线段除外）‎ ‎（2）选择（1）中你所写的一组相等的线段，说说它们相等的理由。‎ 五【教师课后反思】和【学生课后反馈】‎ ‎（老师写下课后的反思，同学们写下你心中的感悟、收获和疑惑）‎ 3‎