8年级数学教案第10讲：阶段性检测

8年级数学教案第10讲：阶段性检测

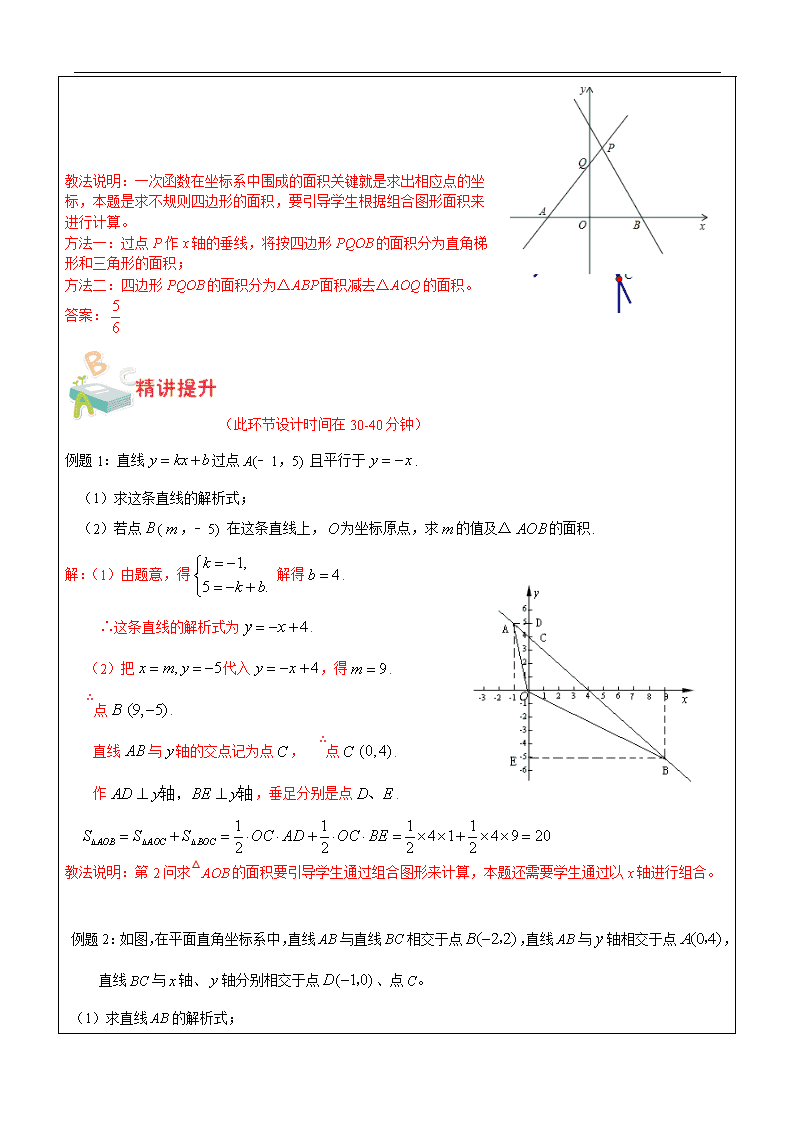
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 阶段性检测 教学内容 1． 掌握一次函数的图形与性质，会求一次函数的解析式；‎ 2． 掌握一次函数与几何图形在坐标轴中围成的面积求法。‎ ‎（此环节设计时间在20-30分钟）‎ 教法说明：通过案例让学生之间相互讨论，解决两个一次函数与坐标轴围成的面积。‎ 案例 问题1：如图，已知直线l：y=﹣2x+2与直线m：y=x交于点T，求直线l 和直线m与x轴所围成的图形面积。‎ 教法说明：通过图形可知，所求图形的面积就是△AOT的面积，先求点A和点T的坐标，可以引导学生求点A和点T的坐标。‎ 答案：A（1，0）； T ‎ 问题2：如图，已知直线l：y=﹣2x+2与x轴、y轴分别交于点B、C，将问题1中的直线m向上平移1个单位长度得到直线PA，点Q是直线PA与y轴的交点，求四边形PQOB的面积。‎ 教法说明：一次函数在坐标系中围成的面积关键就是求出相应点的坐标，本题是求不规则四边形的面积，要引导学生根据组合图形面积来进行计算。‎ 方法一：过点P作x轴的垂线，将按四边形PQOB的面积分为直角梯形和三角形的面积；‎ 方法二：四边形PQOB的面积分为△ABP面积减去△AOQ的面积。‎ 答案：‎ ‎（此环节设计时间在30-40分钟）‎ 例题1：直线过点A(﹣1，5) 且平行于.‎ ‎（1）求这条直线的解析式；‎ ‎（2）若点(，﹣5) 在这条直线上，为坐标原点，求的值及△的面积.‎ 解：（1）由题意，得 解得.‎ ‎∴这条直线的解析式为. ‎ ‎（2）把代入，得. ‎ ‎∴点. ‎ 直线与轴的交点记为点， ∴点. ‎ 作，垂足分别是点. ‎ 教法说明：第2问求△AOB的面积要引导学生通过组合图形来计算，本题还需要学生通过以x轴进行组合。‎ 例题2：如图，在平面直角坐标系中，直线AB与直线BC相交于点，直线AB与轴相交于点，直线BC与轴、轴分别相交于点、点C。‎ ‎（1）求直线AB的解析式；‎ ‎（2）过点A作BC的平行线交轴于点E，求点E的坐标；‎ ‎（3）求△ABC面积。‎ 答案：（1） （2）； （3）6‎ 此环节设计时间在60分钟左右（40分钟练习+20分钟互动讲解）。‎ 一、填空题（本大题共10题，每题4分，满分40分）‎ ‎1．下列函数中：，，，，是一次函数的 有 （填序号）．‎ ‎2．已知直线是一次函数，则的取值范围是 ．‎ ‎3．直线的截距是 ．‎ ‎4．已知函数，随着的增大而 ．‎ ‎5．若直线向下平移个单位后，所得的直线在轴上的截距是，则的值是___________．‎ ‎6．已知直线图像经过第一、三、四象限，则的取值范围是_________．‎ ‎7．已知点A （，2），B （，4）在直线上，则、的大小关系是 ．‎ ‎8．某市为鼓励市民节约用水和加强对节水的管理，制订了以下每月每户用水的收费标准：（1）用水量不超过8时，每立方米收费1元；（2）超出8时，在（1）的基础上，超过8的部分，每立方米收费2元.设某户一个月的用水量为，应交水费元. 则当＞8时，关于的函数解析式是 ．‎ ‎9．与直线平行，且过（0，﹣2）的一次函数的解析式为_____ ______．‎ ‎10．如图，在矩形中，动点从点出发，沿运动至点停止，设点运动的路程为，△的面积为，如果关于的函数关系如图所示，则此矩形的面积是_ ．‎ 二、选择题（本大题共6题，每题4分，满分24分）‎ ‎11．已知直线，在此直线上且位于轴的上方的点，它们的横坐标的取值范围是（ ）‎ ‎ （A）； （B）； （C）； （D）.‎ ‎12．已知一次函数的图像不经过三象限，则、的符号是（ ）‎ ‎ （A）<0，0； （B）<0，0； （C）<0，>0； （D）<0，<0.‎ ‎13．已知一次函数，若函数值随着自变量值的增大而增大，则该函数的图像经过（ ）‎ ‎（A）第一、二、三象限； （B）第一、二、四象限； ‎ ‎（C）第二、三、四象限； （D）第一、三、四象限．‎ ‎14．函数和在同一直线坐标系中的大致图像是（　　　）‎ A B C D ‎15．若直线向下平移个单位后所得的直线在轴上的截距是－2，则的值是（　　　）‎ ‎ A．1 B．‎2 ‎ C．3 D．4‎ ‎16．如图，当x取何值时，函数的图象在第四象限（　 　）‎ ‎ A．‎ ‎ B．‎ ‎ C．‎ ‎ D．‎ 三、解答题：（本大题共4题，每题9分，满分36分） ‎ ‎17．已知一次函数的图像平行于直线，且经过点（2，﹣3）.‎ ‎（1）求这个一次函数的解析式； （2）当=6时，求的值．‎ ‎18．已知一次函数图像经过点A（﹣2，﹣2）、B（0，﹣4）．‎ ‎（1）求、的值；（2）求这个一次函数与两坐标轴所围成的面积．‎ ‎19．若直线分别交轴、轴于A、C两点，点P是该直线上在第一象限内的一点，PB⊥轴，B为垂足，且S⊿ABC= 6．‎ ‎（1）求点B和P的坐标．（2）过点B画出直线BQ∥AP，交轴于点Q，并直接写出点Q的坐标．‎ ‎20．某人因需要经常去复印资料，甲复印社按A4纸每10页2元计费，乙复印社则按A4纸每10页1元计费，但需按月付一定数额的承包费. 两复印社每月收费情况如图所示，根据图中提供的信息解答下列问题：‎ ‎（1）乙复印社要求客户每月支付的承包费是 元．‎ ‎（2）当每月复印 页时，两复印社实际收费相同．‎ ‎（3）如果每月复印页在250页左右时，应选择哪一个复印社？请简单说明理由．‎ 答案：‎ 一、填空题 ‎1． （1），（3）； 2．； 3．﹣4； 4．减小； 5．4； 6．； ‎ ‎7．＜； 8．； 9．； 10．20 .‎ 二、选择题 ‎11．C； 12．A； 13．B； 14．B； 15．C； 16．D；‎ 三、简答题 ‎17．（1） （2）‎ ‎18．（1） （2）8‎ ‎19．（1）A（﹣4，0），C（0，2） 由题意 设点P的坐标为（）且>0‎ ‎∵PB⊥x轴 ∴B（，0） ∴AB=+4‎ ‎∵S⊿ABC=6 ∴‎ ‎∴B（2，0）， P（2，3）‎ ‎（2）图略； ‎ ‎20．（1） 18； （2） 150；‎ ‎（3） 选择乙．当复印页超过150页时，乙的收费较低. ‎ 补充类试题：‎ ‎1．小明申请使用了某移动通信公司的手机来电畅听，这个公司推出的来电畅听业务规定：‎ 用户每月交费16元，可免费接听来电；而打出电话每分钟收费0.13元．‎ ‎（1）小明一个月手机的通话费（包括接听电话和打出电话）y（元）与打出电话时间x（分钟）的解析式为： ；定义域是： ；‎ ‎（2）如果小明某个月的通话费是42元，试求小明该月打出电话的时间．‎ 解：（1）根据题意，得 y = 0.13 x +16，x ≥ 0．‎ ‎ （2）根据题意，得 0.13 x +16 = 42． ‎ ‎ 解得 x = 200．‎ ‎ 答：小明该月打出电话的时间为200分钟．‎ ‎2．如图，与分别是根据步行与骑自行车在同一路上行驶的路程与时间的关系式所作出的图像 ‎（1）出发时与相距_______千米；骑了一段路后，自行车发生故障，进行修理，所用的时间是________小时；从起点出发后_________小时与相遇；‎ ‎（2）写出行走的路程与时间的函数关系式 （不写定义域）；‎ ‎（3）假设的自行车没有发生故障，保持出发时的速度前进，________小时与相遇，相遇点离的出发点__________千米 答案：（1）10，1，3； （2）； （3），‎ ‎3．已知直线y=x+3的图像与x轴、y轴分别交于A、B两点，直线l经过原点，与线段AB交于点C，把△AOB的面积分为2：1两部分，求直线l的解析式．‎ 解：由题意： ∴‎ ‎∴ ∴‎ 代入得，‎ 设直线l的解析式：‎ 代入得 ∴直线l的解析式 同理：,∴直线l的解析式 ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 对本节课的错题进行整理：‎