八年级数学下册知能提升作业二十五第20章平行四边形的判定20

八年级数学下册知能提升作业二十五第20章平行四边形的判定20

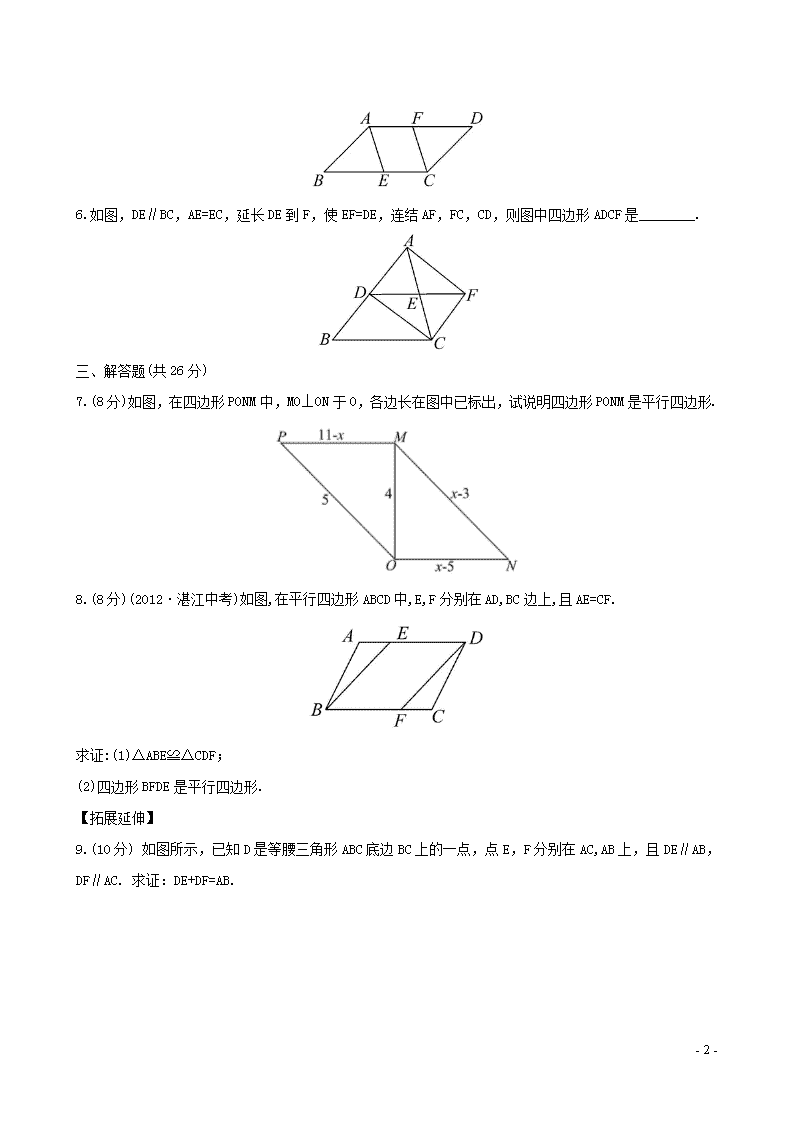
知能提升作业（二十五）‎ 第20章平行四边形的判定20.1平行四边形的判定 ‎ 一、选择题(每小题4分,共12分)‎ ‎1.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )‎ ‎(A)88°,108°,88° (B)88°,104°,108°‎ ‎(C)88°,92°,92° (D)88°,92°,88°‎ ‎2.(2012·巴中中考)不能判定一个四边形是平行四边形的条件是( )‎ ‎(A)两组对边分别平行 ‎(B)一组对边平行，另一组对边相等 ‎(C)一组对边平行且相等的 ‎(D)两组对边分别相等 ‎3.在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，那么 还不能判定四边形ABCD为平行四边形，给出的以下四个说法中，正确的说法 有( )‎ ‎(1)如果再加上条件“AD∥BC”，那么四边形ABCD一定是平行四边形；‎ ‎(2)如果再加上条件“AB=CD”，那么四边形ABCD一定是平行四边形；‎ ‎(3)如果再加上条件“∠DAB=∠DCB”,那么四边形ABCD一定是平行四边形；‎ ‎(4)如果再加上条件“AO=CO”，那么四边形ABCD一定是平行四边形.‎ ‎(A)4个 (B)3个 ‎ ‎(C)2个 (D)1个 二、填空题(每小题4分,共12分)‎ ‎4.如图，在□ABCD中，E,G是AD的三等分点，F,H是BC的三等分点，则图中的平行四边形共有______个.‎ ‎5.(2012·龙东中考)如图,在平行四边形ABCD中,点E,F分别在BC,AD上,请添加一个条件_______使四边形AECF是平行四边形(只填一个即可).‎ - 4 -‎ ‎6.如图，DE∥BC，AE=EC，延长DE到F，使EF=DE，连结AF，FC，CD，则图中四边形ADCF是________.‎ 三、解答题(共26分)‎ ‎7.(8分)如图，在四边形PONM中，MO⊥ON于O，各边长在图中已标出，试说明四边形PONM是平行四边形.‎ ‎8.(8分)(2012·湛江中考)如图,在平行四边形ABCD中,E,F分别在AD,BC边上,且AE=CF.‎ 求证:(1)△ABE≌△CDF；‎ ‎(2)四边形BFDE是平行四边形.‎ ‎【拓展延伸】‎ ‎9.(10分) 如图所示，已知D是等腰三角形ABC底边BC上的一点，点E，F分别在AC,AB上，且DE∥AB，DF∥AC. 求证：DE+DF=AB.‎ - 4 -‎ ‎.‎ 答案解析 ‎1.【解析】选D.当四边形的三个内角度数依次为88°,92°,88°时,第四个角的度数为92°.由同旁内角互补,两直线平行,得四边形的两组对边分别平行,四边形为平行四边形.‎ ‎2.【解析】选B.A,C,D选项都是正确的,B选项不一定是平行四边形.‎ ‎3.【解析】选A.根据平行四边形的判定方法知，①②正确.对于③，∵AB∥CD,∴∠DAB+∠ADC=180°，∠DCB+∠ABC=180°,又∵∠DAB=∠DCB,‎ ‎∴∠ADC=∠ABC,∴四边形ABCD为平行四边形，故③正确.对于④，‎ ‎∵AB∥CD,∴∠BAO=∠DCO,∠ABO=∠CDO,又AO=CO，∴△ABO≌△CDO，‎ ‎∴OB=OD，∴四边形ABCD为平行四边形，故④正确.‎ ‎4.【解析】∵四边形ABCD为平行四边形 ‎∴ADBC,又E,G和F,H分别为AD,BC的三等分点,∴AE=EG=GD=BF=FH=HC，故此题中的四边形全部为平行四边形，故平行四边形有□ABFE,□ABHG，□ABCD，‎ ‎□EFHG，□EFCD和□GHCD共六个.‎ 答案：6‎ ‎5【解析】答案不唯一,如添加的条件是AF=CE.理由是:‎ ‎∵四边形ABCD是平行四边形,‎ - 4 -‎ ‎∴AD∥BC,∴AF∥CE,‎ ‎∵AF=CE,∴四边形AECF是平行四边形.‎ 答案：AF=CE(或E,F分别是BC,AD的中点或AE∥CF，答案不唯一)‎ ‎6.【解析】∵AE=EC，EF=DE,∴四边形ADCF为平行四边形.‎ 答案：平行四边形 ‎7.【解析】在Rt△MON中，由勾股定理，得42+(x-5)2=(x-3)2，解得x=8，所以11-x=3，x-5=3，x-3=5，所以PM=ON，PO=MN，所以四边形PONM是平行四边形.‎ ‎8.【证明】(1)∵四边形ABCD是平行四边形,‎ ‎∴∠A=∠C,AB=CD,‎ 在△ABE和△CDF中,‎ ‎∵∴△ABE≌△CDF(S.A.S.).‎ ‎(2)∵四边形ABCD是平行四边形,‎ ‎∴AD∥BC,AD=BC,‎ ‎∵AE=CF,∴AD-AE=BC-CF,‎ 即DE=BF,∴四边形BFDE是平行四边形.‎ ‎9.【证明】∵DE∥AB，DF∥AC,‎ ‎∴四边形AEDF是平行四边形，‎ ‎∴DF=AE.‎ 又∵DE∥AB，∴∠B=∠EDC，‎ 又∵AB=AC,∴∠B=∠C，‎ ‎∴∠C=∠EDC，∴DE=CE，‎ ‎∴DF+DE=AE+CE=AC=AB.‎ - 4 -‎