初中数学8年级教案：第10讲 平行四边形的判定

初中数学8年级教案：第10讲 平行四边形的判定

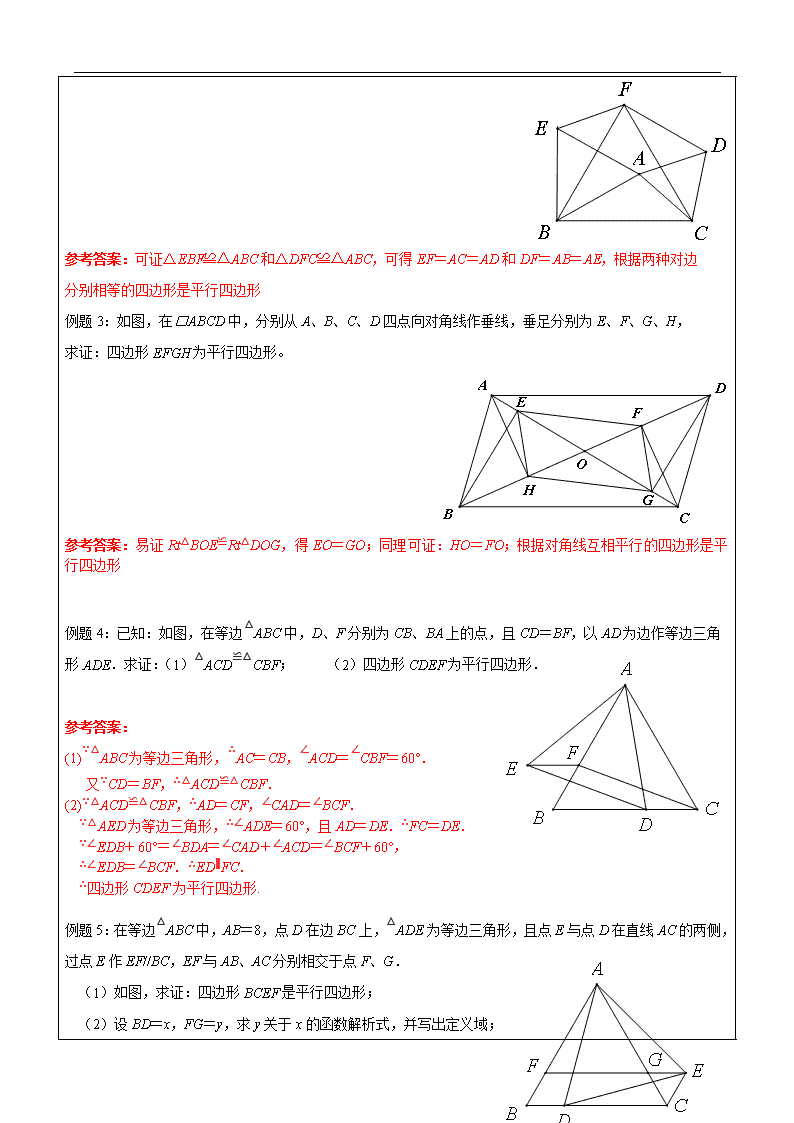
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目：‎ 授课日期 ‎××年××月××日 时 间 A / B / C / D / E / F段 主 题 平行四边形的判定 教学内容 ‎1．掌握平行四边形判定定理； ‎ ‎2．会应用平行四边形的性质定理和判定定理解决相关的几何证明和计算问题．‎ ‎（此环节设计时间在10-15分钟）‎ 教法说明：首先回顾上次课的预习思考内容，归纳总结平行四边形的判定．‎ 回顾平行四边形的判定 ‎ 平行四边形判定定理 边 ‎（1）两组对边分别平行 ‎（2）两组对边分别相等 ‎（3）一组对边平行且相等 角 ‎（4）两组对角分别相等 对角线 ‎（5）对角线互相平分 ‎1．能判定四边形ABCD是平行四边形的条件是：∠A∶∠B∶∠C∶∠D的值为（ ）．‎ A、1∶2∶3∶4 B、1∶4∶2∶3‎ C、1∶2∶2∶1 D、1∶2∶1∶2‎ ‎2．如图，E、F分别是□ABCD的边AB、CD的中点，则图中平行四边形的个数共有（ ）．‎ A、2个 B、3个 C、4个 D、5个 ‎3．已知：四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下四种说法：‎ ‎①如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；‎ ‎②如果再加上条件“∠BAD＝∠BCD”，那么四边形ABCD一定是平行四边形；‎ ‎③如果再加上条件“OA＝OC”，那么四边形ABCD一定是平行四边形；‎ ‎④如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形．其中正确的说法是（ ）．‎ A、①② B、①③④ C、②③ D、②③④‎ ‎4．在四边形ABCD中，AB∥CD，如果要使这个四边形成为平行四边形，那么还需添加一个条件，这个条件可以是 ．‎ 参考答案：1．D； 2．C； 3．C； 4． AB＝CD（答案不唯一）‎ ‎（此环节设计时间在50-60分钟）‎ 例题1：已知：如图，□ABCD中，平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N，交 BA﹑BC于点P、Q，求证：MP＝NQ 参考答案：可证四边形ACQM和四边形ACNP为平行四边形，可得MQ＝AC＝NP 例题2：如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．‎ 求证：四边形ADFE为平行四边形；‎ 参考答案：可证△EBF≌△ABC和△DFC≌△ABC，可得EF＝AC＝AD和DF＝AB＝AE，根据两种对边分别相等的四边形是平行四边形 例题3：如图，在□ABCD中，分别从A、B、C、D四点向对角线作垂线，垂足分别为E、F、G、H，‎ 求证：四边形EFGH为平行四边形。‎ 参考答案：易证Rt△BOE≌Rt△DOG，得EO＝GO；同理可证：HO＝FO；根据对角线互相平行的四边形是平行四边形 例题4：已知：如图，在等边△ABC中，D、F分别为CB、BA上的点，且CD＝BF，以AD为边作等边三角 形ADE．求证：（1）△ACD≌△CBF； （2）四边形CDEF为平行四边形．‎ 参考答案：‎ ‎(1)∵△ABC为等边三角形，∴AC＝CB，∠ACD＝∠CBF＝60°．‎ 又∵CD＝BF，∴△ACD≌△CBF．‎ ‎(2)∵△ACD≌△CBF，∴AD＝CF，∠CAD＝∠BCF．‎ ‎∵△AED为等边三角形，∴∠ADE＝60°，且AD＝DE．∴FC＝DE．‎ ‎∵∠EDB＋60°＝∠BDA＝∠CAD＋∠ACD＝∠BCF＋60°，‎ ‎∴∠EDB＝∠BCF．∴ED∥FC．‎ ‎∴四边形CDEF为平行四边形.‎ 例题5：在等边△ABC中，AB＝8，点D在边BC上，△ADE为等边三角形，且点E与点D在直线AC的两侧，过点E作EF//BC，EF与AB、AC分别相交于点F、G．‎ ‎（1）如图，求证：四边形BCEF是平行四边形；‎ ‎（2）设BD＝x，FG＝y，求y关于x的函数解析式，并写出定义域；‎ ‎※（3）如果AD的长为7时，求线段FG的长．‎ 参考答案：（1）证明：∵△ABC和△ADE是等边三角形，‎ ‎∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60º．‎ ‎∴∠BAD＝∠CAE．∴△BAD≌△CAE．‎ ‎∵∠B＝∠ACB＝60º，∴∠ACE＝∠B＝60º，∠BCE＝120º．‎ ‎∴∠B＋∠BCE＝180º，∴BF//CE．‎ ‎∵EF//BC，∴四边形BCEF是平行四边形． ‎ ‎（2）解：∵四边形BCEF是平行四边形，△BAD≌△CAE，∴BF＝CE＝BD＝x，‎ ‎∵EF//BC，∴∠AGF＝∠ACB＝60º＝∠FAG，‎ ‎∴FG＝AF＝8—x，‎ ‎∴y关于x的函数解析式为，定义域为．‎ ‎ （3）解：过点A作AH⊥BC，垂足为H， BH＝BC＝8， ∴，‎ DH＝．‎ 当时，FG＝8—3＝5．‎ 当时，FG＝8—5＝3．‎ 此环节设计时间在30分钟左右（20分钟练习＋10分钟互动讲解）。‎ ‎1．已知：如图，□OCDE和□ABCD；其中点O是□ABCD的对角线AC与BD的交点；‎ 求证：OE与AD互相平分．‎ 参考答案：联结AE，证四边形AODE为平行四边形（一组对边平行且相等）‎ ‎2．已知：如图，点E、G在平行四边形ABCD的边AD上，EG＝ED，延长CE到点F，使得EF＝EC．‎ 求证：AF∥BG．‎ 参考答案：联结FG，GC，FD，分别证明四边形CDFG和ABGF为平行四边形即可．‎ ‎3．如图，在□中，、交于点，、的中点分别是、．‎ 求证：四边形是平行四边形．‎ 参考答案：根据对角线互相平分即可证明．‎ ‎4．如图，在□ABCD中，∠DAB＝60°，点E、F分别在CD、AB的延长线上，且AE＝AD，CF＝CB．‎ ‎（1）求证：四边形AFCE是平行四边形；‎ ‎（2）若去掉已知条件的“∠DAB＝60°”，上述的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由 参考答案：（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴DC∥AB，∠DCB＝∠DAB＝60°．‎ ‎∴∠ADE＝∠CBF＝60°． ∵AE＝AD，CF＝CB，‎ ‎∴△AED，△CFB是正三角形．‎ ‎∴∠AEC＝∠BFC＝60°，∠EAF＝∠FCE＝120°．‎ ‎∴四边形AFCE是平行四边形．‎ ‎（2）解：上述结论还成立．‎ 证明：∵四边形ABCD是平行四边形，‎ ‎∴DC∥AB，∠CDA＝∠CBA，∠DCB＝∠DAB，AD＝BC，DC＝AB．‎ ‎∴∠ADE＝∠CBF． ∵AE＝AD，CF＝CB，‎ ‎∴∠AED＝∠ADE，∠CFB＝∠CBF． ∴∠AED＝∠CFB．‎ 又∵AD＝BC， ‎ 在△ADE和△CBF中．∠ADE＝∠CBF，∠AED＝∠CFB，AD＝BC ‎∴△ADE≌△CBF（AAS）．‎ ‎∴∠AED＝∠BFC，∠EAD＝∠FCB．‎ 又∵∠DAB＝∠BCD，‎ ‎∴∠EAF＝∠FCE．∴四边形EAFC是平行四边形．‎ ‎（此环节设计时间在5-10分钟内）‎ 让学生回顾本节课所学的重点知识，以学生自我总结为主，学科教师引导为辅，为本次课做一个总结回顾 ‎【巩固练习】‎ ‎1．如图，在平行四边形ABCD中，E、F分别在CD、AB上，且AF＝CE，FG⊥AD于G，EH⊥BC于H．‎ 求证：四边形EGFH为平行四边形．（运用两种以上的方法证明）‎ 参考答案：‎ 方法1：先证△AGF≌△CHE得FG＝EH，AG＝CH，再证△GDE≌△HBF得GE＝FH，从而四边形EGFH为平行四边形 方法2：延长GF交BC于M，可证GF∥EH，再证△AGF≌△CHE得FG＝EH，从而四边形EGFH为平行四边形 ‎2．如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别是E、F.求证：四边形AECF是平行四边形.‎ 参考答案：由已知证得AE∥CF；由△ABE≌△DCF证得AE＝CF ‎3．如图在Rt△ABC中，∠C＝90°，M是AB中点，AM＝AN，MN∥AC，求证：MN＝AC 参考答案：联结CM，证明四边形ACMN为平行四边形 ‎4．已知：如图，oABCD中，．求证： EN∥MF．‎ ‎ ‎ 参考答案：证明四边形EMFN为平行四边形（一组对边平行且相等）‎ ‎【预习思考】‎ ‎1．回顾矩形和菱形除了具备平行四边形的性质以外的特殊性质，完成下表；‎ 边 角 对角线 对称性 矩形 菱形 ‎2.总结一下矩形和菱形的判定，完成下表；‎ 矩形的判定 菱形的判定 四边形矩形 四边形菱形 平行四边形矩形 平行四边形菱形