北师大版八年级下册数学同步练习课件-第6章-4 多边形的内角和与外角和（二）

北师大版八年级下册数学同步练习课件-第6章-4 多边形的内角和与外角和（二）

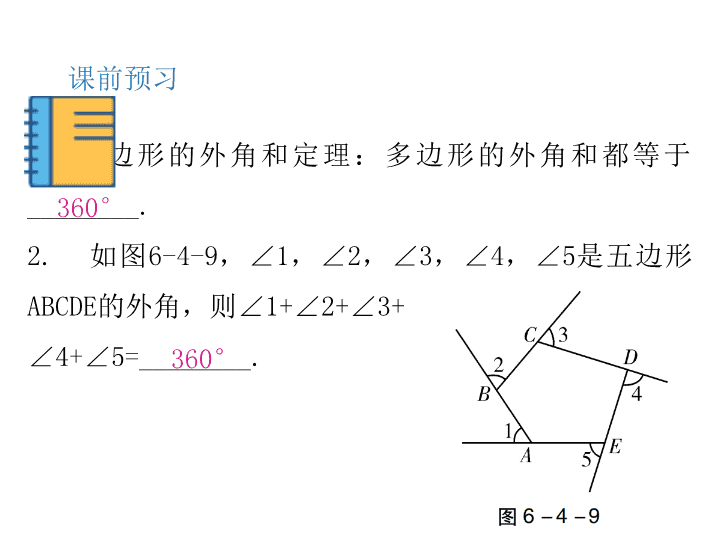
中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源中小学精品教学资源 4多边形的内角和与外角和第六章平行四边形第2课时多边形的内角和与外角和（二） 课前预习1.多边形的外角和定理：多边形的外角和都等于________.2.如图6-4-9，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，则∠1+∠2+∠3+∠4+∠5=________.360°360° 3.若一个多边形的内角和是外角和的3倍，则这个多边形的边数是（）A.10B.9C.8D.64.若一个正多边形的每一个外角为30°，那么这个正多边形的边数是（）A.6B.8C.10D.12CD 课堂讲练典型例题新知：多边形的外角和定理【例1】八边形的外角和为（）A.180°B.360°C.1080°D.1440°B 模拟演练1.正十边形的每个外角的度数是（）A.360°B.36°C.30°D.135°B 典型例题【例2】一个多边形的每个内角都相等，并且它的一个外角与一个内角的比为1∶3，则这个多边形为（）A．三角形B．四边形C．六边形D．八边形D 模拟演练2.若一个多边形的每个外角都等于它的相邻内角的14，则这个多边形的边数是（）A.12B.10C.8D.6B 【例3】如图6-4-10，在五边形ABCDE中，若∠D=100°，则∠1+∠2+∠3+∠4=_________.典型例题280° 3.如图6-4-11，在五边形ABCDE中，AB∥CD，∠1，∠2，∠3是五边形的外角，则∠1+∠2+∠3等于________.模拟演练180° 【例4】在各个内角都相等的多边形中，一个内角是与它相邻的一个外角的3倍，求这个多边形的每一个外角的度数及这个多边形的边数.典型例题解:每一个外角的度数是180°÷4=45°.360°÷45°=8，则这个多边形是八边形. 4.一个多边形，它的内角和比外角和的4倍多180°，求这个多边形的边数及内角和的度数.模拟演练解：设多边形的边数为n.根据题意，得（n-2）·180=360×4+180,即（n-2）·180=1620.解得n=11.答：这个多边形的边数是11，内角和是1620°. 分层训练1.一个正多边形的内角和为540°，则这个正多边形的每个外角的度数等于（）A.60°B.72°C.90°D.108°2.正n边形的每一个外角都不大于40°，则满足条件的多边形边数最少为（）A.7B.8C.9D.10BC 3.下列内角和与外角和相等的多边形是（）4.已知一个多边形的内角和与外角和的差是1260°，则这个多边形的边数是______.C11 5.内角和与外角和之比是5∶1的多边形是_______边形.6.一个n边形的所有内角与所有外角的和是900°，那么n=______.十二5 7.当多边形每增加一条边时，它的（）A．外角和与内角和都增加180°B．外角和与内角和都增大180°C．外角和增大180°，内角和不变D．外角和不变，内角和增大180°D 8.设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（）A.a＞bB.a=bC.a＜bD.b=a+180°B 9.如图6-4-12，一个六边形ABCDEF的六个内角都是120°，连续四边的长依次为AB=1，BC=3，CD=3，DE=2，那么这个六边形ABCDEF的周长是（）A．12B．13C．14D．15D 10.在计算一个多边形的内角和时，粗心的小明没有将其中一个内角加上去，而是加上了这个内角所对应的外角，这样计算出来的结果是600°，则小明计算的这个多边形的边数为__________．5或6 C组11.如图6-4-13，求∠A+∠B+∠C+∠D+∠E+∠F的度数.解：∵∠BPO是△PDC的外角，∴∠BPO=∠C+∠D.∵∠POA是△OEF的外角，∴∠POA=∠E+∠F.∵∠A+∠B+∠BPO+∠POA=360°，∴∠A+∠B+∠C+∠D+∠E+∠F=360°. 12.在一个多边形中，一个内角相邻的外角与其他各内角的和为600°.（1）如果这个多边形是五边形，请求出这个外角的度数；（2）是否存在符合题意的其他多边形？如果存在，请求出边数及这个外角的度数；如果不存在，请说明理由. 解：（1）设这个外角的度数是x°.依题意，得（5-2）×180-（180-x）+x=600.解得x=120.答：这个外角的度数是120°. （2）存在.设边数为n，这个外角的度数是x°.依题意，得（n-2）×180-（180-x）+x=600.整理，得x=570-90n.∵0＜x＜180，即0＜570-90n＜180，并且n为正整数，∴n=5或n=6.∴n=6,x=570-90×6=30.答：这个多边形的边数是6，这个外角的度数为30°.