七年级下册数学同步练习第五章 相交线与平行线周周测7（5-4） 人教版

七年级下册数学同步练习第五章 相交线与平行线周周测7（5-4） 人教版

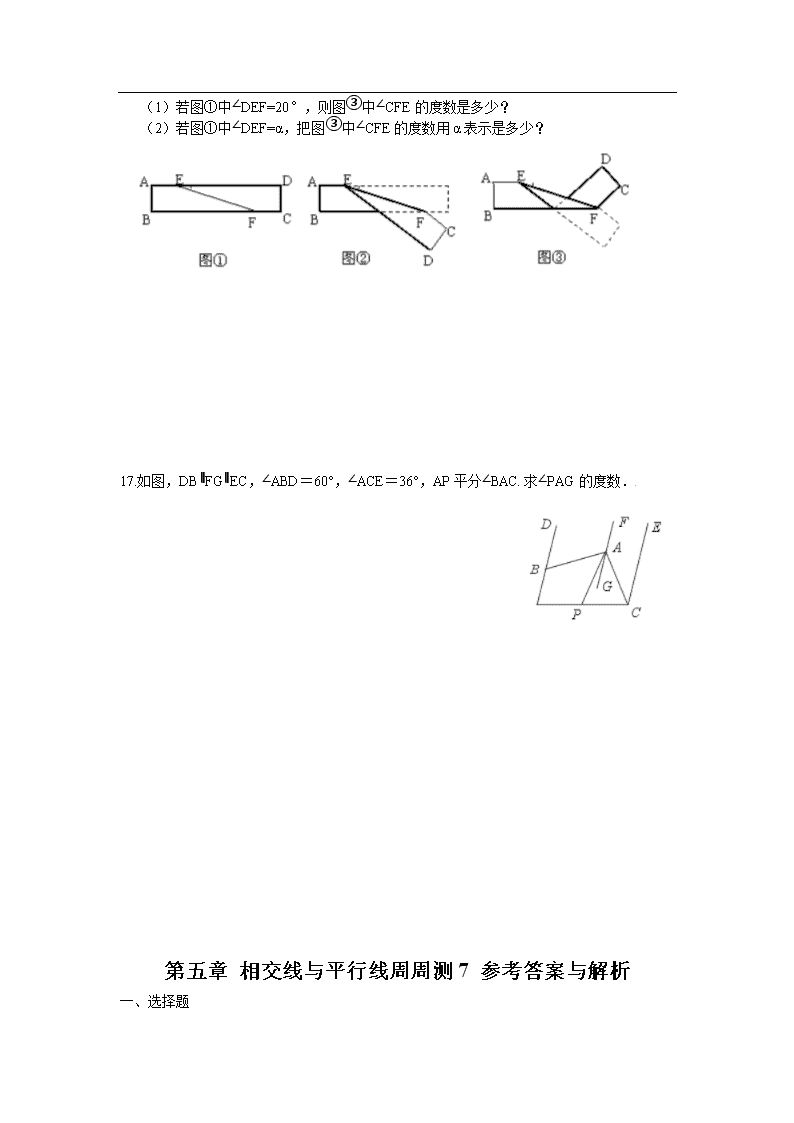
第五章 相交线与平行线周周测7‎ 一 选择题 ‎1.将图①所示的图案通过平移后可以得到的图案是（   ）‎ ‎ A B C D 图①‎ ‎2.在5×5方格纸中将图①中的图形N平移后的位置如图②所示，那么下面平移中正确的是（   ）‎ ‎    A. 先向下移动1格，再向左移动1格  B. 先向下移动1格，再向左移动2格 ‎    C. 先向下移动2格，再向左移动1格  D. 先向下移动2格，再向左移动2格 ‎ ‎ ‎ 第2题图 第3题图 ‎ ‎3.如图，已知三角形ABC的面积为8，将三角形ABC沿BC的方向平移到三角形A’B’C’的位置，使B’和C重合，连结AC’交A’C于D，则三角形CAC’的面积为 （ ）‎ ‎ A．4　            B．6            C．8           D． 16 ‎ ‎4.四根火柴棒形成如图所示的“口”字，平移火柴棒后，原图形能变成的汉字是(   )‎ ‎ ‎ ‎5.如图，面积为12cm²的三角形ABC沿BC方向平移至三角形DEF的位置，平移的距离是边BC的2倍，则图中四边形ACFD的面积为（    ）‎ ‎ A．24cm²              B．36cm²                    C．48cm²                  D．60cm²‎ ‎ [来源:学科网ZXXK]‎ ‎ 第5题图 第6题图 ‎6.如图，小明从家到学校有①②③三条路可走，每条路的长分别为a，b，c，则（      ）‎ ‎ A.              B.              C.              D.‎ ‎7.从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积是（    ）‎ ‎ A．20            B．22             C．24               D．26 ‎ ‎ [来源:学科网]‎ 第7题图 第8题图 ‎8.如图，将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形，至少需要移动（　 ）‎ ‎ Ａ.8格        Ｂ.9格         Ｃ.11格         Ｄ.12格 二 填空题 ‎9.如图，将三角形ABC沿BC方向平移2cm得到三角形DEF，若三角形ABC周长为16cm，则四边形ABFD周长为 ．‎ ‎ ‎ ‎ 第9题图 第10题图 第11题图 ‎10.如图，将三角形ABC沿射线AC平移得到三角形DEF.若AF=17，DC=7，则AD= .‎ ‎11.如图，边长为8cm的正方形ABCD先向上平移4cm，再向右平移2cm，得到正方形A′B′C′D′，此时阴影部分的面积为_________.‎ ‎12.某小区的一块长26米，宽15米的草坪内要修一条如图所示宽度相同的通道.当通道的宽度为2米时，剩下的草坪面积是通道面积的 倍．                                     ‎ ‎ ‎ ‎ 第12题图 第13题图 第14题图 ‎13. 鑫都大酒店在装修时，准备在主楼梯（如图）上铺上红地毯，已知这种地毯每平方米售价35元.楼梯宽2米，则购买这种地毯至少需 元.‎ ‎14.如图，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG=24cm，WG=8cm，WC=6cm，求阴影部分的面积为　　　　　　cm2．‎ 三 解答题 ‎15.如图，已知，AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠AEF，∠1＝40°，求∠2的度数．‎ ‎16.如图①是长方形纸带，将纸带沿EF折叠成图②，再沿BF折叠成图③.‎ ‎ （1）若图①中∠DEF=20°，则图③中∠CFE的度数是多少？‎ ‎      （2）若图①中∠DEF=α，把图③中∠CFE的度数用α表示是多少？‎ ‎[来源:Zxxk.Com]‎ ‎17.如图，DB∥FG∥EC，∠ABD＝60°，∠ACE＝36°，AP平分∠BAC.求∠PAG的度数．‎ ‎[来源:Zxxk.Com]‎ 第五章 相交线与平行线周周测7 参考答案与解析 一、选择题 ‎1.A 2.C 3.C 4.B 5.C 6.C 7.C 8.A ‎ 二、填空题 ‎9.20 10.5 11.24cm² 12.4 13.630 14.168 ‎ 三、解答题 ‎15.解：∵AB∥CD，∠1＝40°，∴∠AEG=∠1=40°. ‎ ‎∵EG平分∠AEF，，∴∠AEF=2∠AEG=80°，∴∠2=180°-∠AEF=180°-80°=100°.‎ ‎[来源:Zxxk.Com]‎ ‎16.解：图①中，∵AD∥BC，∴∠DEF=∠BFE，∴∠CFE=180°-∠DEF.‎ 图②中，由折叠得∠CEF=180°-∠DEF，∴∠CFB=∠CEF-∠BFE=180°-2∠DEF.‎ 图③中，由折叠得∠CFB=180°-2∠DEF，∴∠CFE=∠CFB-∠BFE=180°-3∠DEF.‎ ‎（1）若图①中∠DEF=20°，则图③中∠CFE=180°-3×20°=120°.‎ ‎（2）若图①中∠DEF=α，则图③中∠CFE=180°-3α.‎ ‎17.解：∵DB∥FG∥EC，∠ABD＝60°，∠ACE＝36°，∴∠BAG=∠ABD＝60°，∠CAG=∠ACE＝36°，∴∠BAC=∠BAG+∠CAG=60°+36°=96°.‎ ‎∵AP平分∠BAC，∴∠PAC=∠BAC=×96°=48°，∴∠PAG=∠PAC-∠CAG=48°-36°=12°.‎