探索三角形全等的条件教案(1)(2)

探索三角形全等的条件教案(1)(2)

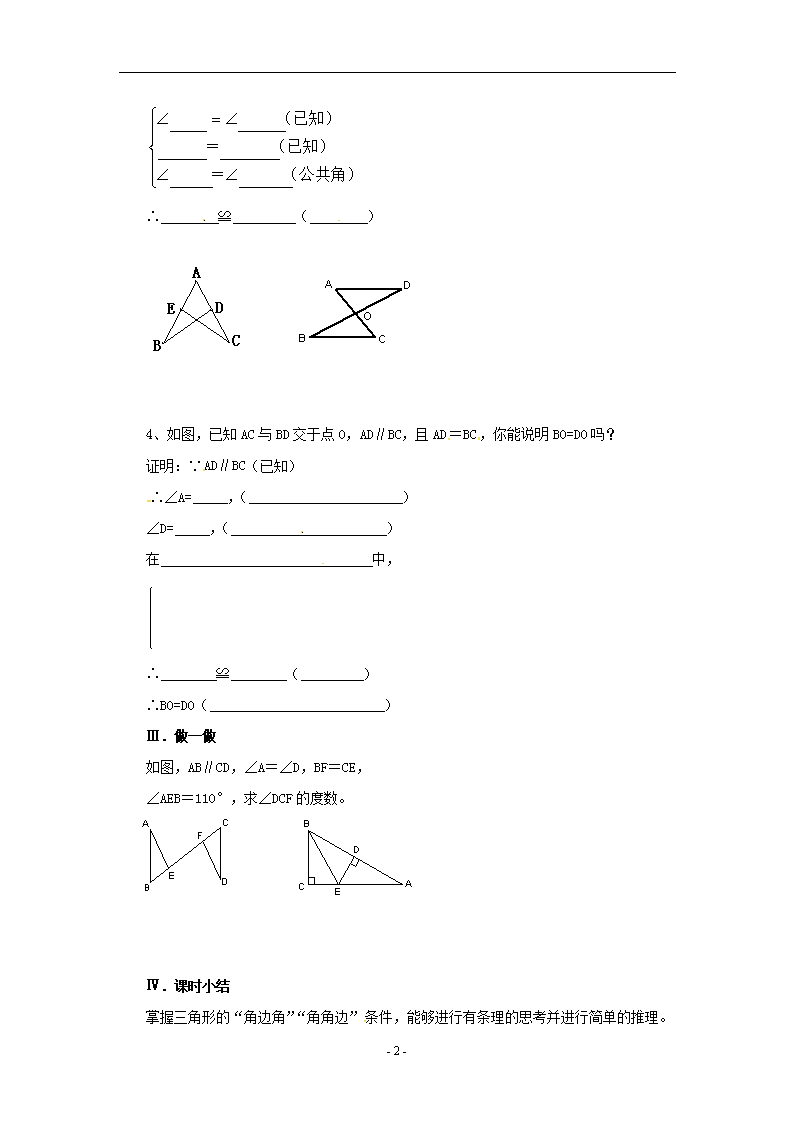
‎ ‎ 探索三角形全等的条件（2）‎ ‎〖教学目的：〗‎ ‎〖知识与技能目标：〗‎ ‎1．经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；‎ ‎2．掌握三角形的“角边角”“角角边”条件，了解三角形的稳定性。‎ ‎〖过程与方法：〗‎ 在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理。‎ ‎〖情感态度与价值观：〗‎ 通过动手作图，让学生接触事物、感之事物，获得请、亲身体验和直接经验，从中发现问题。‎ ‎〖教学重点、难点：〗‎ 重点：三角形“角边角”“角角边”的全等条件。‎ 难点：用三角形“角边角”“角角边”的条件进行有条理的思考并进行简单的推理。‎ ‎〖授课时间：〗‎ Ⅰ.创设现实情景，引入新课 ‎1．如果“两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60°和80°，它们所夹的边为2cm，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？‎ ‎2．如果“两角及一边”条件中的边是其中一角的对边，比如三角形两个内角分别是60°和45°，一条边长为3cm。你画的三角形与同伴画的一定全等吗？‎ Ⅱ．根据现实情景，讲授新课 一．结论：‎ 两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”‎ 两角和其中一角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”‎ 二．巩固练习：‎ ‎1、两角和它们的夹边对应相等的两个三角形全等，简写成 或 ‎ ‎2、两角和其中一角的对边对应相等的两个三角形全等，简写成 或 ‎ ‎3、如图，AB＝AC，∠B＝∠C，你能证明△ABD≌△ACE吗？‎ 证明： △ABD和△ACE中 - 3 -‎ ‎ ‎ ‎∴ ≌ （ ）‎ ‎4、如图，已知AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO=DO吗？‎ 证明：∵AD∥BC（已知）‎ ‎∴∠A= ，（ ）‎ ‎∠D= ，（ ）‎ 在 中，‎ ‎∴ ≌ （ ）‎ ‎∴BO=DO（ ）‎ Ⅲ．做一做 如图，AB∥CD，∠A＝∠D，BF＝CE，‎ ‎∠AEB＝110°，求∠DCF的度数。‎ Ⅳ．课时小结 掌握三角形的“角边角”“角角边”条件，能够进行有条理的思考并进行简单的推理。‎ - 3 -‎ ‎ ‎ Ⅴ．课后作业 P164 习题5．8‎ ‎〖板书设计：〗‎ 探索三角形全等的条件（2）‎ 两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”‎ 两角和其中一角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”‎ VI．教学后记 - 3 -‎