- 2021-10-21 发布 |
- 37.5 KB |
- 10页


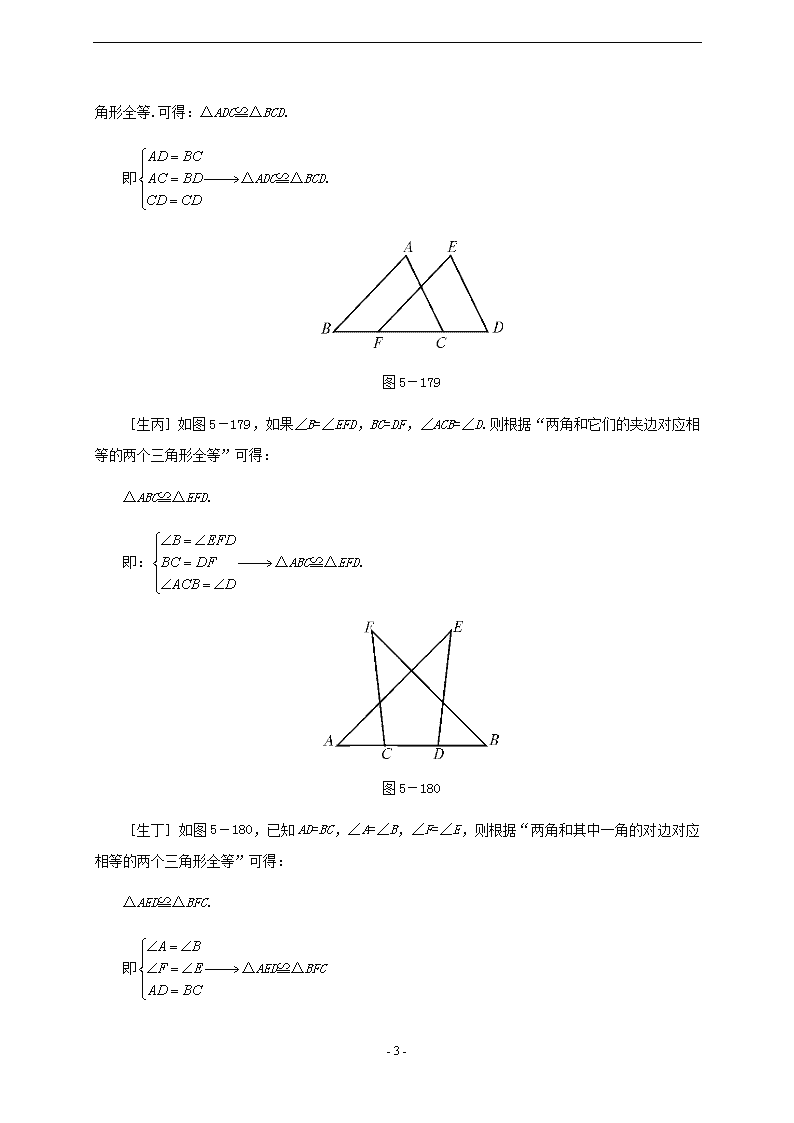
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第五章 三角形 复习教案
北师版七下《第3章 三角形》教案 ●教学目标 (一)教学知识点 1.判断三角形全等的条件. 2.判断两个直角三角形全等的条件. 3.利用尺规作一个三角形与已知三角形全等. 4.全等图形及其他在生活中的应用. (二)能力训练要求 1.使学生进一步了解图形的全等,能利用全等图形进行简单的图案设计. 2.通过回顾使学生掌握两个三角形全等的条件,能应用三角形的全等解决一些实际问题. 3.在分别给出两角夹边,两边夹角和三边的条件下,能够利用尺规作出三角形. 4.尝试用图形(案)表达自己的想法,发展基本的创新意识和能力. (三)情感与价值观要求 1.通过回顾的活动,进一步发展学生的空间观念,使其积累数学活动经验. 2.在活动过程中,使学生进一步体会数学与现实的密切联系. ●教学重点 三角形全等的条件及其应用. 直角三角形全等的条件及其应用. 尺规作图. ●教学难点 两个三角形全等的应用. 两个直角三角形全等的应用. - 10 - ●教学方法 分组讨论法 学生在教师的指导下分组讨论、归纳、梳理本章的知识体系,从而使学生顺利掌握本章内容. ●教具准备 投影片两张 第一张:问题串(记作投影片“回顾与思考(二)”A) 第二张:知识框架图(记作投影片“回顾与思考(二)”B) ●教学过程 Ⅰ.巧设现实情景,引入新课 [师]通过上节课的回顾复习,我们进一步了解了三角形的有关概念及三边、三角之间的关系,那么两个三角形之间又如何呢?这节课我们共同来复习三角形的全等. Ⅱ.讲授新课 [师]下面我们通过问题形式,来回顾三角形全等这部分内容(出示投影片“回顾与思考(二)”A) 1.举出生活中包含全等图形的例子. 2.举例说明怎样判断两个三角形全等?怎样判断两个直角三角形全等? 3.举例说明三角形全等在生活中的应用. 4.利用尺规,你能用几种方法作一个三角形与已知三角形全等? [师]大家分组讨论后,回答问题. [生甲]一栋楼房的所有窗户是全等图形.它的阳台也是全等图形. …… 图5-178 [生乙]如图5-178,如果AD=BC,AC=BD,则由于CD - 10 - 是公共边,根据三边对应相等的两个三角形全等.可得:△ADC≌△BCD. 即△ADC≌△BCD. 图5-179 [生丙]如图5-179,如果∠B=∠EFD,BC=DF,∠ACB=∠D.则根据“两角和它们的夹边对应相等的两个三角形全等”可得: △ABC≌△EFD. 即:△ABC≌△EFD. 图5-180 [生丁]如图5-180,已知AD=BC,∠A=∠B,∠F=∠E,则根据“两角和其中一角的对边对应相等的两个三角形全等”可得: △AED≌△BFC. 即△AED≌△BFC - 10 - 图5-181 [生戊]如图5-181,如果已知AB=AE,AC=AD,则由于∠A是公共角,可根据“两边和它们的夹角对应相等的两个三角形全等”得:△ABC≌△AED. 即△ABC≌△AED. [生子]要判断两个直角三角形全等,除应用一般三角形的判定方法外,还可用“斜边、直角边”.即:斜边和一条直角边对应相等的两个直角三角形全等. 图5-182 如图5-182,已知:在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AC=A′C′,AB=A′B′则可得出:Rt△ABC≌Rt△A′B′C′ [师]同学们总结得真棒,由以上方法可以判断两个三角形全等.这些方法要灵活应用. 在生活中经常会遇到一些问题需要利用三角形全等来解决,你能举出一些例子吗? [生]如:测量河宽时,需要构造三角形全等来解决. …… [师]很好,大家举出许多的例子说明三角形全等在生活中的应用.你能用尺规作一个三角形与已知三角形全等吗? - 10 - [生甲]能,可以利用两角夹边、两边夹角、三边、直角边和斜边等方法来作一个三角形与已知三角形全等. [生乙]只有作直角三角形时,才能用“直角边和斜边”,一般三角形不能. [师]很好,接下来我们分组讨论,梳理本章的知识框架. [师生共析]下面我们共同来建立本章的知识框架(出示投影片“回顾与思考”(二)B) [师]好,接下来我们通过练习进一步巩固本章的内容. Ⅲ.课堂练习 课本P157复习题A组 4、5、6、7、8 4.如图5-183,△ADB≌△EDB,△BDE≌△CDE,B、E、C在一条直线上. (1)BD是∠ABE的平分线吗?为什么? (2)DE⊥BC吗?为什么? (3)点E平分线段BC吗?为什么? 图5-183 答:(1)BD是∠ABE的平分线.因为△ADB≌△EDB根据“全等三角形的对应角相等”可得: - 10 - ∠ABD=∠DBE.由角平分线的定义可知:BD平分∠ABE,即:BD是∠ABE的平分线. (2)DE垂直BC,因为△BDE≌△CDE.由“全等三角形的对应角相等”可知:∠BED=∠DEC.又因为B、E、C在一条直线上,所以∠DEB+∠DEC=180°.因此∠DEB=∠DEC=90°,即:DE⊥BC. (3)点E平分线段BC,因为△BDE≌△CDE所以由“全等三角形的对应边相等”可得:BE=EC,即:点E是BC的中点. 图5-184 5.如图5-184,BE⊥AE,CF⊥AE,垂足分别是E、F,D是EF的中点,△BED与△CFD全等吗?为什么? 解:△BED与△CFD全等.因为: △CFD≌△BED. 6.尺规作图,已知线段a和∠α. 图5-185 (1)作一个三角形ABC,使AB=3a,BC=4a,AC=5a. - 10 - (2)作一个三角形,使BC=a,AC=2a,∠BAC=∠α. 作法:(1): 图5-186 ①作一条线段AC=5a. ②分别以A、C为圆心,以3a,4a为半径画弧,两弧交于B点. ③连接AB、BC. 则:△ABC就是所求作的三角形. (2) 图5-187 ①作一条线段AC=2a. ②以点C为顶点,以AC为一边,作角∠DCA=∠α. ③在射线CD上截取CB=a. ④连接AB. 则△ABC就是所求作的三角形. 7.工人师傅经常利用角尺平分一个任意角,如图5-188所示,∠AOB是一个任意角,在边OA,边OB上分别取OD=OE,移动角度,使角尺两边相同的刻度分别与D、E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线,你能先说明△OPE与△OPD全等,再说明OP平分∠AOB吗? - 10 - 图5-188 答:因为OD=OE,PE=PD,OP=OP,所以根据“三边对应相等的两个三角形全等”可得:△OPE≌△OPD.从而由“全等三角形的对应角相等”可得:∠BOP=∠AOP.即: OP平分∠AOB. Ⅳ.课时小结 这节课我们主要回顾了三角形全等的条件及其应用. 大家在判定两个三角形全等或应用全等三角形性质时,应注意找到它们的对应元素;再就是应学会分析. Ⅴ.课后作业 (一)课本P159复习题B组1~4 C组1、2. (二)用自己的语言梳理本章内容,即:写一份小结. Ⅵ.活动与探究 - 10 - 图5-189 如图5-189,△ABC中,AF是∠EAC的平分线,D是这条平分线上任意一点,试确定AB+AC和BD+DC之间的大小关系,并说明理由. 分析:让学生讨论、分析,知道要探求线段大小关系往往把这些线段归结到同一个三角形中,利用三角形三条边的关系求得.这个题可根据角平分线条件构造全等三角形.即在射线AE上截取AC′=AC,连接C′D,可得△AC′D≌△ACD(SAS)从而得:C′D=CD.于是就把这四条线段放入一个三角形中,它们的大小即可求得. 结果:AB+AC小于BD+DC. 图5-190 如图所示5-190:在射线AE上截取AC′=AC,连接C′D. AF是∠EAC的平分线 ●板书设计 回顾与思考(二) 一、问题串 二、知识框架图 - 10 - 三、课堂练习 四、课时小结 - 10 -查看更多