初中数学7年级教案：第14讲 等边三角形

初中数学7年级教案：第14讲 等边三角形

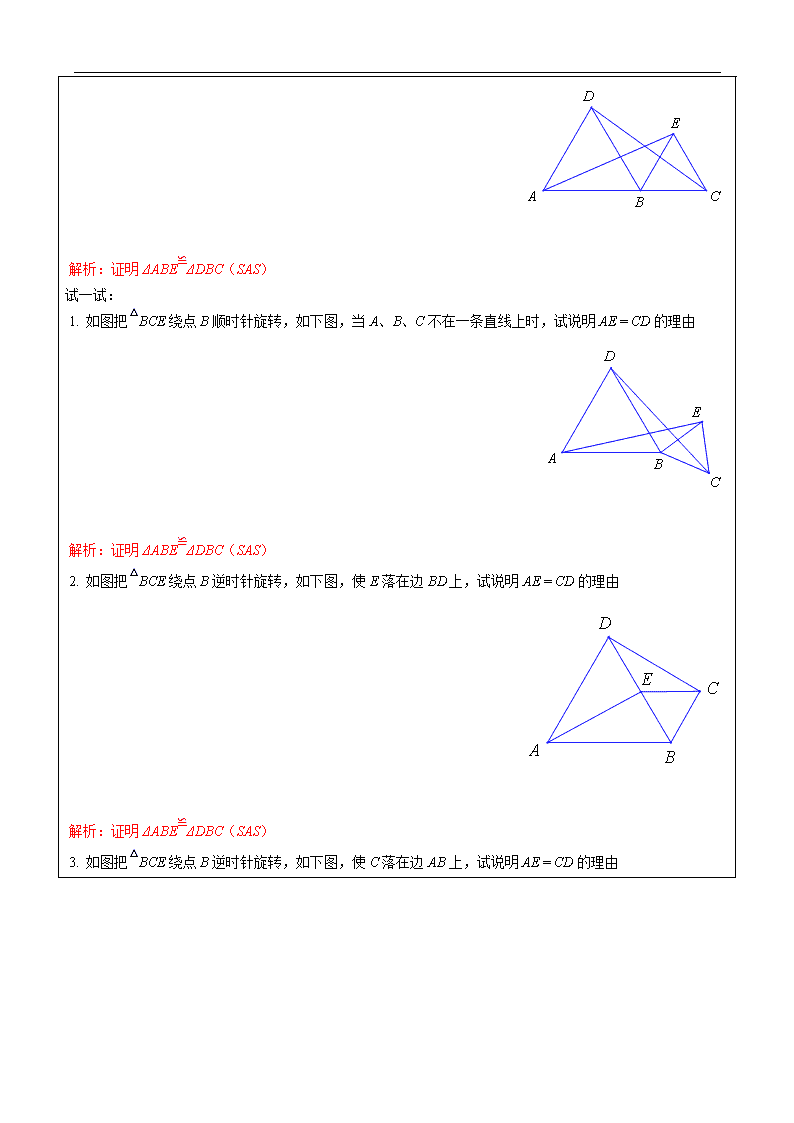
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 等边三角形 教学内容 ‎1．理解等边三角形是特殊的等腰三角形，是轴对称性图形；‎ ‎2．掌握等边三角形的性质，能够较熟练地利用“等边对等角”及有关特征解决相关问题；‎ ‎（以提问的形式回顾）‎ ‎1. 等边三角形性质有哪些？‎ ‎（1）具备等腰三角形的左右性质 ‎（2）等边三角形的三条边都相等，三个内角都等于60°‎ ‎2. 等边三角形的判定：‎ ‎（1）三条边相等的三角形是等边三角形 ‎（2）三个内角相等的三角形是等边三角形 ‎（3）有一个内角是60°的等腰三角形是等边三角形 小练习 ‎1．延长等边ΔABC的边BC到D，使CD = BC，那么ΔABD是 ( )‎ ‎ A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形 ‎2．如图，在ΔABC中，∠C = 120°，∠A = 45°，D在BC上，直线AD将这个三角形分成两个等腰三角形，则∠CDA的度数是 ( )‎ ‎ A、20° B、30°‎ ‎ C、45° D、15°‎ ‎3．下列说法中错误的是 ( )‎ A、等腰三角形是锐角三角形 B、等腰直角三角形是直角三角形 C、等边三角形是等腰三角形 D、等边三角形是锐角三角形 ‎4．D是等边ΔABC边AC上一点，∠ACE = ∠ABD，CE = BD，则ΔADE是 ( )‎ ‎ A、钝角三角形 B、直角三角形 C、任意等腰三角形 D、等边三角形 ‎5．如图，ΔABC和ΔCDE均为等边三角形，A、E、D在同一直线上，且∠EBD = 62°，则∠AEB的度数是 ( )‎ A、112° B、122° C、132° D、128°‎ 参考答案：1、A； 2、B； 3、A； 4、D； 5、B ‎（采用教师引导，学生轮流回答的形式）‎ 例1. 如图，A、B、C三点在一直线上，分别以AB、BC为边在AC同侧作等边ΔABD和等边ΔBCE，联结AE，CD。‎ 问题1：试说明AE = CD的理由。‎ 解析：证明ΔABE≌ΔDBC（SAS）‎ 试一试：‎ ‎1. 如图把△BCE绕点B顺时针旋转，如下图，当A、B、C不在一条直线上时，试说明AE = CD的理由 解析：证明ΔABE≌ΔDBC（SAS）‎ ‎2. 如图把△BCE绕点B逆时针旋转，如下图，使E落在边BD上，试说明AE = CD的理由 解析：证明ΔABE≌ΔDBC（SAS）‎ ‎3. 如图把△BCE绕点B逆时针旋转，如下图，使C落在边AB上，试说明AE = CD的理由 解析：证明ΔABE≌ΔDBC（SAS）‎ 问题5：如下图，A、B、C三点在一直线上，分别以AB、BC为边在AC同侧作等边ΔABD和等边ΔBCE，联结AE，CD，MN，判定△MBN的形状以及MN和AC的位置关系。‎ 解析：先证明ΔABE≌ΔDBC（SAS）得到∠BAE=∠BDC，‎ 再证明ΔABM≌ΔDBN（ASA）得到BM=BN，所以△MBN为等边三角形，‎ MN∥AC 例2. 如图，在△中，已知，点、、分别在边、、上，且，．‎ ‎（1）说明△与△全等的理由．‎ ‎（2）如果△是等边三角形，那么△是等边三角形吗？试说明理由．‎ 解 ：（1）记，．‎ 因为（三角形的一个外角等于与它不相邻的两个内角和），‎ 即．‎ ‎ 又因为（已知），‎ 所以（等式性质）．‎ 因为（已知），‎ 所以（等边对等角）．‎ ‎ 在△和△中，‎ ‎ ‎ ‎ 所以△≌△（AAS），‎ ‎（2）因为△≌△，‎ ‎ 所以（全等三角形的对应边相等）．‎ 因为△是等边三角形（已知），‎ ‎ 所以（等边三角形的每个内角等于60°）． ‎ ‎ 因为（已知），‎ ‎ 所以（等量代换）．‎ ‎ 所以△是等边三角形（有一个内角等于的等腰三角形是等边三角形）．‎ 例3. 如图，D为等边ΔABC内一点，DB=DA，BE=AB，∠DBE=∠DBC，求∠BED的度数。‎ 解析：联结DC，先证明ΔACD≌ΔBCD（SSS） 得到∠ACD=∠BCD=30°‎ 再证明ΔEBD≌ΔCBD（SAS）得到∠BED=∠BCD=30°‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ ‎1．如图，已知△ABC中，AB=AC，分别以AB、AC为边作等边△ABE、等边△ACD，且∠DAE=∠BCD，求∠BAC的度数．‎ 答案：∠BAC=20°‎ ‎2．如图，在等边△ABC边AC上取一点D，使BD=CE，∠ABD=∠ACE， 求证：△ADE是等边三角形．‎ 解析：ΔABD≌ΔACE（SAS）即可 ‎3．如图，在等边ΔABC的AC、BC边上各取一点E、F，使AE = CF，AF与BE交于点O，‎ 求∠BOF的度数。‎ 答案：∠BOF=60°，证明ΔABE≌ΔACF（SAS）‎ ‎4．如图，等边△中，点在边上，CE∥AB，且CE＝AD，‎ ‎（1）△是什么特殊三角形，请说明理由．‎ ‎（2）如果点在边的中点处，那么线段与有怎样的位置关系，请说明理由．‎ ‎ ‎ 解： （1）△是等边三角形． ‎ 说理如下：‎ 记，， ‎ 因为△是等边三角形（已知），‎ 所以（等边三角形的三边都相等），‎ ‎（等边三角形的每个内角都等于）．‎ 因为（已知），‎ 所以（两直线平行，内错角相等）．‎ 所以（等量代换）‎ 在△和△中， ‎ ‎ ‎ ‎ 所以△≌△（SAS），‎ 得（全等三角形的对应角相等），‎ ‎ （全等三角形的对应边相等）‎ 又因为 所以 即 所以△是等边三角形（有一个内角等于的等腰三角形是等边三角形）‎ ‎（2）线段与的位置关系是：‎ 说理如下：‎ 因为，‎ 所以（等腰三角形的三线合一）‎ 因为 所以 又因为 所以（等腰三角形的三线合一）‎ ‎ ‎ 本节课主要知识点：等边三角形的判定与性质，等边三角形与全等三角形综合 ‎【巩固练习】‎ 1． 如图，ΔABC和ΔDEC均为等边三角形，∠EAB = 40°，∠ACE = 25°，‎ 求∠BDC的度数 解析：∠BEC=135°，证明ΔACE≌ΔBCD，得到∠AEC=∠BDC ‎2．如图，D是等边ΔABC的边AB上的一点，以CD为边作等边ΔCDE，联结AE，‎ 求证：AE∥BC 解析：证明ΔBCD≌ΔACE，得到∠DBC=∠EAC=60°即可 ‎3．如图，在△ABC三边作三个等边三角形△ACD、△ABE、△BCF．‎ 证明：AE = D F 解析：证明ΔABC≌ΔDFC，得到DF=AB即可 ‎【预习思考】‎ ‎1. 平行线的性质与判定：‎ ‎2. 全等三角形的性质：‎ ‎3. 三角形全等的判定定理：‎