江苏省苏州市2019-2020高一数学下学期学业质量调研试题（Word版附答案）

江苏省苏州市2019-2020高一数学下学期学业质量调研试题（Word版附答案）

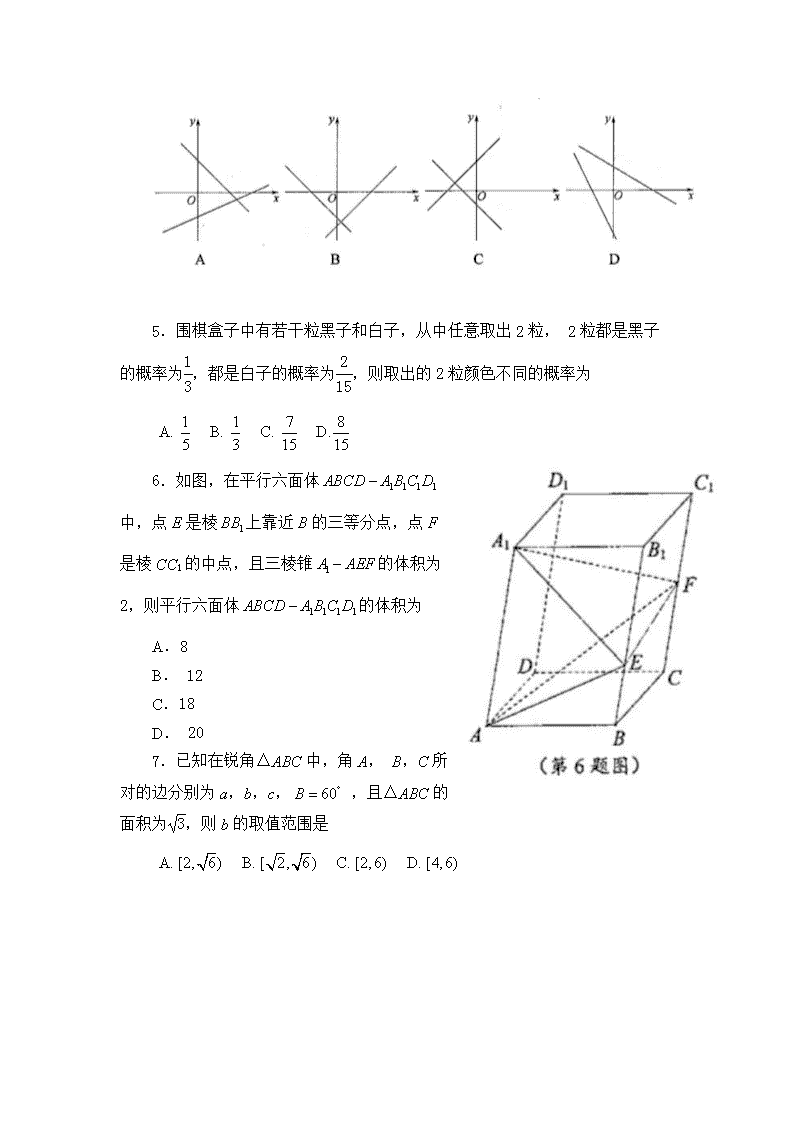
苏州市 2019—2020 学年第二学期学业质量阳光指标调研卷 高一数学 2020．7 注意事项 学生在答题前请认真阅读本注意事项及各题答题要求： 1．本卷共 6 页，包含单项选择题（第 1 题——第 8 题）、多项选择题（第 9 题—第 12 题）、填空题（第 13 题——第 16 题）、解答题（第 17 题——第 22 题），本卷满分 150 分，答题时问为 120 分钟，答题结束后，请将答题卡交回． 2．答题前，请您务必将自己的姓名、调研序列号用 0．5 毫米黑色墨水的签 字笔填写在答题卡的规定位置． 3．请在答题卡上按照顺序在对应的容题区域内作答，在其他位置作答一律 无效，作答必须用 0．5 毫米黑色墨水的签字笔，请注意字体工整，笔迹清楚． 一、单项选择题：本大题共 8 小题，每小题 5 分，共计 40 分，每小题给出 的四个选项中，只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位 置上． 1．已知圆锥的底面半径为 4，母线长为 5，则该圆锥的侧面积为 16 B. 20 D C.. 40 36 .A     2．苏州市 6 月 1 日起正式实施的《生活垃圾分类管理条例》将城市生活垃 圾分为“可回收物”、“有害垃圾”、“厨余垃吸”和“其他垃圾”四人类．某社区为了 分析不同年龄段的人群对垃圾分类知识的了解情况，对辖区内的居民进行分层抽 样调查．已知该社区的青年人、中年人和老年人分别有 800 人、900 人、700 人， 若在老年人中的抽样人数是 35，则在青年人中的抽样人数是 A．20 B．40 C． 60 D． 80 3．从 1，2，3，4，5 这五个数中任取两个数，则这两个数之和等于 5 的概 率为 1 1 1 2. B. C. D. 20 10 5 5A 4．在同一平面直角坐标系中，两直线 1x y m n   与 1x y n m   的图象可能是 5．围棋盒子中有若干粒黑子和白子，从中任意取出 2 粒， 2 粒都是黑子的 概率为1 3 ，都是白子的概率为 2 15 ，则取出的 2 粒颜色不同的概率为 1 1 7 8 A. B. C. 5 D3 1 .5 5 1 6．如图，在平行六面体 1 1 1 1ABCD A B C D 中， 点 E 是棱 1BB 上靠近 B 的三等分点，点 F 是棱 CC1 的中点，且三棱锥 1A AEF 的体积为 2，则 平行六面体 1 1 1 1ABCD A B C D 的体积为 A．8 B． 12 C．18 D． 20 7．已知在锐角△ABC 中，角 A， B，C 所 对的边分别为 a，b，c， 60B  ，且△ABC 的 面积为 3，则 b 的取值范围是 A. [2, 6) B. [ 2, 6) C. [2,6) D. [4,6) 8．在平面立角坐标系 xOy 中，两圆 1 2,O O 均过点（3，0） ，它们的圆心分 别为 1 2( ,0),( ,0)x x ，满足 1 2 1 1 2 3x x   ，若两圆与 y 轴正半轴分别交于 1 2(0, ),(0, )y y ， 则 1 2y y 的值为 A．2 B．6 C． 9 D．与 1 2,x x 的取值有关 二、多项选择题：本大题共 4 小题，每小题 5 分，共计 20 分，每小题给出 的四个选项中，都有多个选项是正确的，全部选对的得 5 分，选对但不全的得 3 分，选错或不答的得 0 分、请把正确的选项填涂在答题卡相应的位置上． 9．党的十九大为新时代农业农村改节发展明确了重点、指明了方向，报告 中提出了“实施乡村振兴战略”．某地区农村经过三年的乡村振兴建设，农村的经 济收入增加了一倍。为更好地了解该地区农村的经济收入变化情况，统计了该地 区实施乡村振兴建设前后农村的经济收入构成比例，得到如下饼图： 则下面结论中正确的有 A．乡村振兴建设后，种植收入减少 B．乡村振兴建设后，其他收入增加了倍以上 C．乡村振兴建设后，养殖收入增加了一倍 D．乡村振兴建设后，养殖收入与第三产业收入的总和超过了经济收入的一 半 10．已知函数 ( ) sin(2 )6f x x   在区间[ ,0]a 上单调递增，则实数 a 的可能 值为 3 A. B. C. D. 8 4 8 2     11．在△ABC 中，角 A，B，C 所对的边分别为 a，b，c．已知 2 3, 3b B    ， 若添加下列条件来解三角形，则其中三角形只有一解的是 7 9 A. 3 B. C. 4 D. 2 2c c c c    12．如图，点 E 是正方体 1 1 1 1ABCD A B C D 的棱 DD1 的中点，点 M 在线段 BD1 上运动，则下列结论正确的是 A．直线 AD 与直线 C1M 始终是异而直线 B．仔在点 M，使得 B1M⊥AE C．四面体 EMAC 的体积为定值 D．当 1 2D M MB 时，平面 EAC⊥平面 MAC 三、填空题：本大题共 4 小题，每小题 5 分，共计 20 分，请把答案填写在答题卡相应位置上． 13．为抗击新型冠状病毒，普 及防护知识，某校开展了“疫情防 护”网络知识竞赛活动，现从参 加该活动的学生中随机抽取了 100 名学生，将 他们的比赛成绩 （满分为 100 分）分为 5 组： [50， 60) ， [60，70) ， [70， 80) ， [80 ，90) ，[90 ， 100]， 得到如图所示的频率分布直方图， 则该100名学生中成绩在 80分（含 80 分）以上的人数为________ 14．在△ABC 中，角 A，B， C 所对的边分别为 a，b，c，若 13, 2,cos 3a b C   ，则△ABC 的面积为________ 15．已知 A， B 两点分别在两条互相垂立的直线 2x－y＝0 和 x＋ay＝5 上， 且线段 AB 的中点为 P(0，5)，则|AB|＝________ 16．已知在球 O 的内接长方体 1 1 1 1ABCD A B C D 中， 1 2, 3AB AA AD   ， 则球 O 的表面积为________，若 P 为线段 AD 的中点，则过点 P 的平面截球 O 所得截面面积的最小值为________． （本小题第一空 2 分，第二空 3 分） 四、解答题：本大题共 6 小题，共计 70 分，请在答题卡指定区域内作答， 解答时应写出文字说明、证明过程或演算步骤． 17． （本小题满分 10 分） 如图，在斜三棱柱 1 1 1ABC A B C 中，已知 AB AC ， M，N 分别为 BC， AC 的中点，侧面 1 1A ACC 是菱形， 1 60A AC   （1）求证： AB∥平面 A1MN； (2)求证：平面 1 1A ACC ⊥平面 A1MN． 18． （本小题满分 12 分） 已知圆 C 经过两点 (1, 1), ( 1,1)P Q  ，且圆心 C 在直线 x＋y－2－0 上． （1）求圆 C 的方程； （2）过点 M（0，3）的直线 l 与圆 C 相交于 A，B 两点，且| | 2 3AB  求直 线 l 的方程． 19． （本小题满分 12 分） 随着我国中医学的发展，药用昆虫的需求愈米愈多．每年春暖花开后，昆虫 大量繁殖．研究发现某类药用昆虫的个体产则数 y（单位：个）与温度 x（单位：℃） 有关，科研人员随机挑选了 3 月份中的 5 天进行研究，收集了 5 组观测数据如下 表： 科研人员确定的研究方案是：先用前三组数据建立 y 关于 x 的线性回归方程， 再用后两组数据进行检验． （1）求 y 关于 x 的线性回归方程； （2）若由线性回归方程行到后两组的估计数据与实际观测数据的误差均不 超过 2 个，则认为线性同归方程足可靠的，试问（1）中所得的线性回归方程是 否可靠？ （附：回归直线的斜率和截距的公式分别为 1 2 1 ( )( ) ˆ ˆˆ, ( ) n i i i n i i x x y y b a y bx x x           20． （本小题满分 12 分） 在① cos 0b A c  ， @ cos cosa B b A ， ③ cos 0a C b  这三个条件中选 择符合题意的一个条件，补充在下面的问题中，并求解。 在△ABC 中，角 A，B，C 的对边分别为 a．b，c．已知 2, 4b c  ，满足 ________ （1）请写出你的选择，并求出角 A 的值； （2）在（1）的结论下，已知点 D 在线段 BC 上，且 3 4ADB   ，求 CD 长． 21． （本小题满分 12 分） 如图所示，等边三角形 ABC 的边长为 3，点 D，E 分别是边 AB， AC 上的 点，满足 AD＝1， DE⊥AB．将△ADE 沿 DE 折起到△A1DE 的位置，使二面 1A DE B  为二面角，连接 1 1,A B AC ． （1）求二面角 1C A B D  的余弦值； （2）线段 A1E 上是否存在点 P，使得直线 CP 与平面 A1BC 所成的角为 60°？ 若存在，求出 A1P 的长；若不存在，请说明理由． 22． （本小题满分 12 分） 如图，点 0 0( , )P x y 是圆 2 2: 9O x y  上一动点，过点 P 作圆 0 的切线 l 与圆 2 2 1 :( ) ( 4) 100( 0)O x a y a     交于 A，B 两点，已知当直线 l 过圆心O1时， 1| | 4O P  (1)求 a 的值； （2）当线段 AB 最短时，求直线 l 的方程； (3)问：满足条件! | | 1 | | 3 AP BP  的点 P 有几个?请说明理由．