- 2021-06-23 发布 |
- 37.5 KB |
- 7页

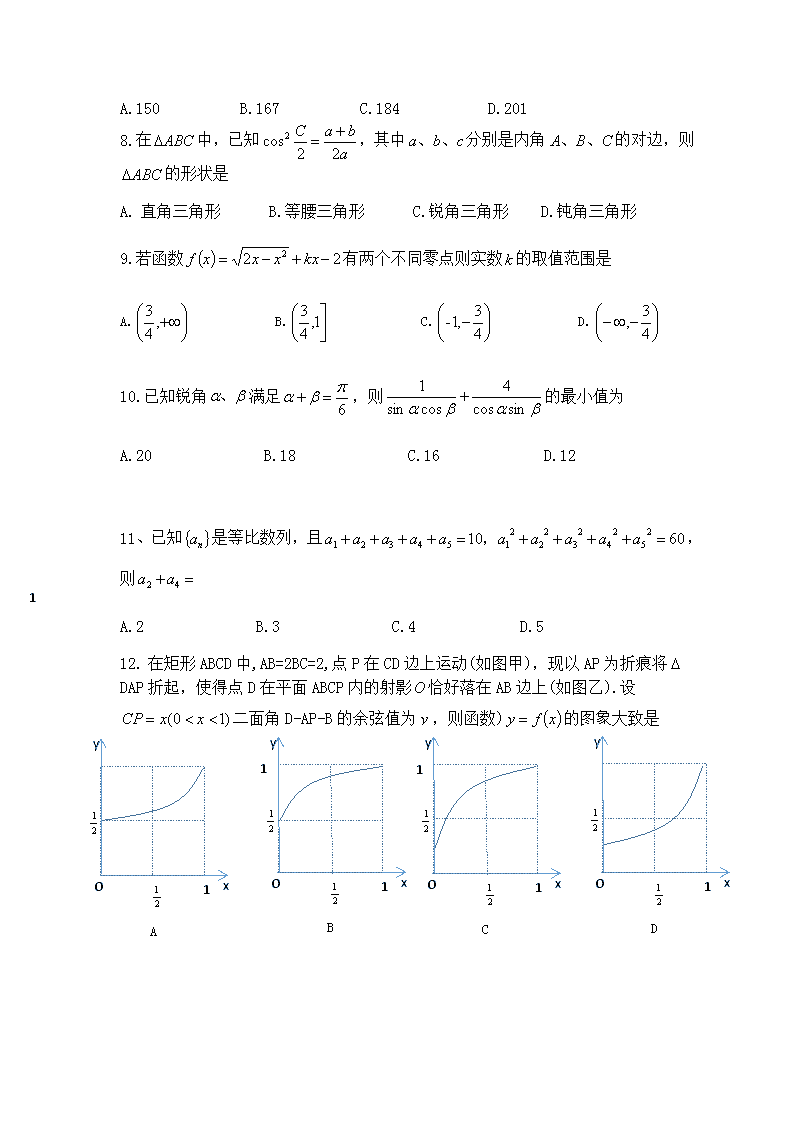

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
四川省成都市第七中学2019-2020高一数学下学期期末试题(Word版附答案)
成都七中期末高一下期末考试 1.设 ba ,则下列不等式一定成立的是 A. ba B. ba 11 C. 22 ba D. ba 22 2.直线 1 62 yx 的倾斜角大小为 A. 6 B. 3 C. 3 2 D. 6 5 3.设 、、 是三个不同平面,l 是一条直线,下列各组条件中可以推出 // 的有 ① ll , ② //,// ll ∥ ③ //,// ④ , A.①③ B.①④ C.②③ D.②④ 4.已知 2,0 ,且 2sin6sin5 ,则 2tan A. 3 4 B. 4 3 C. 4 3 D. 3 4 5.已知直线 02 2 1 ayaxl: 与直线 0112 ayxal : 互相平行,则实数 a 的值为 A.-1 B.0 C.1 D.2 6.若存在实数 yx, 满足 ayx yx yx yx 2 13 1 3 ,则实数 a 的取值范围是 A. 2,1 B. 3,1 C. 4,1 D. 4,2 7.在我国明代数学家“珠算之父”程大位(1533-1606)所著的《算 法统宗》中,有许多用诗歌形式表达的数学问题,如八子分棉 歌:“九百九十六斤棉,赠分八子做盘缠,次第每人多十七,要将 第八数来言,务要分明依次第,孝和休惹外人传.”则此问题(第八 数)的答案为(单位:斤) A.150 B.167 C.184 D.201 8.在 ABC 中,已知 a baC 22cos2 ,其中 cba 、、 分别是内角 CBA 、、 的对边,则 ABC 的形状是 A. 直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形 9.若函数 22 2 kxxxxf 有两个不同零点则实数k 的取值范围是 A. ,4 3 B. 1,4 3 C. 4 3,1- D. 4 3, 10.已知锐角 、 满足 6 ,则 sincos 4 cossin 1 的最小值为 A.20 B.18 C.16 D.12 11、已知 na 是等比数列,且 6010 2 5 2 4 2 3 2 2 2 154321 aaaaaaaaaa , , 则 42 aa A.2 B.3 C.4 D.5 12. 在矩形 ABCD 中,AB=2BC=2,点 P 在 CD 边上运动(如图甲),现以 AP 为折痕将 DAP 折起,使得点 D 在平面 ABCP 内的射影O恰好落在 AB 边上(如图乙).设 )10( xxCP 二面角 D-AP-B 的余弦值为 y ,则函数) xfy 的图象大致是 1 2 1 y x1 2 1O A 2 1 y x1 2 1O B 1 2 1 y x1 2 1O C 1 2 1 y x1 2 1O D 二、填空题:本题共 4 小题,每小题 5 分,共 20 分. 13.已知 245tan ,则 2tan ________. 14.已知 Nn ,若数列 na 的前 n 项和 2nS ,则 n ________. 15.长方体 1111 DCBAABCD 中, BCAB 2 ,设 E 为 AB 的中 点,直线 ED1 与底面 ABCD成 45 角,则异面直线 ED1 与 BC 所成角的 大小为________. 16. 在平面直角坐标系 xOy 中,已知圆 RyxC 2sincos 22: . ①圆C 与圆 1: 22 yxO 的位置关系是________; (选填:相离,外切,相交,内切或内含) ②记圆 C 与直线 02:02: 21 yxlyxl 和 分别交于 CA、 和 DB、 四点,当 变化时, 凸四边形 ABCD面积的最大值是________.(第①问:2 分,第②问:3 分) 三、解答题:本题共 6 小题,70 分.解答应写出文字说明、证明过程或演算步骤. 17.(10 分)已知函数 2,2,,2sincos Rxxxxf 其中 (1)若 02 f ,求角 的大小; (2)当 3 时,求 xf 的最大值. P 图甲 D C A B D P C BA O 图乙 18.(12 分)如图,在四棱锥 ABCDP 中,已知底面 ABCD是菱形. (1)若 PDPB ,求证:平面 PACPBD 面 ; (2)设 E 为 BC 的中点,且 MPDM 2 ,求证: //PB 平面 MAE ,并求 平面 MAE 与棱 PC 的交点 N 的位置. 19、如图,海面上一走私船正以每小时 15 海里的速度沿方位 角 120º方向航行,距离走私船 18 海里处的缉私艇测得该走私 船当前的方位角为 60º,并即刻以每小时 21 海里的速度径 直追赶. (1)求缉私艇追上走私船所需的最短时间; (2)求缉私艇用时最短的追赶方向(方位角 )的余弦值 20、已知定义在 R 上的函数 kxxxf 2)( ,其中k 为常数。 (1)求解关于 x 的不等式 kxxf )( 的解集; (2)若 2f 是 af 与 bf 的等差中项,求 ba 的取值范围。 21.已知数列 na 的前 n 项和 nS 满足 NnaS nn 132 (1)求数列 na 的通项公式; (2)设点列 nnn baP , 都在函数 xy 3log 的图像上,依次连结 1321 nPPPP 、、 形成 折线 L 。记折线 L 对应的函数为 xfy ,求不等式组 xfy axa n 0 11 所表示的平面区 域的面积 22.(12 分)已知圆C 经过坐标原点O 和点 2,2G ,且圆心C 在直线 02 yx 上. (1)求圆C 的方程; (2)设 PBPA、 是圆C 的两条切线,其中 BA、 为切点. ①若点 P 在直线 02 yx 上运动,求证:直线 AB 经过定点; ②若点 P 在曲线 44 1 2 xxy 其中 上运动,记直线 PBPA、 与 x 轴的交点分别为 NM、 , 求 PMN 面积的最小值. 一、选择题 D C A D B CCABB AD 二、填空题 13、 4 3 ; 14、99; 15、60º; 16、①相交; (2 分) ②3. (3 分) 三、解答题 17、1) 6 (2) 2max xf 18、略 19、(2)2 小时 (2) 7 1 20、(1)略 (2) 4,2ba 21、(2) n na 3 (2) 13 n n nT 22、(1) 0422 yyx (2)直线 AB 经过定点 1,1 ; PMN 面积的最小值 32查看更多