2005年浙江省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

2005年浙江省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】

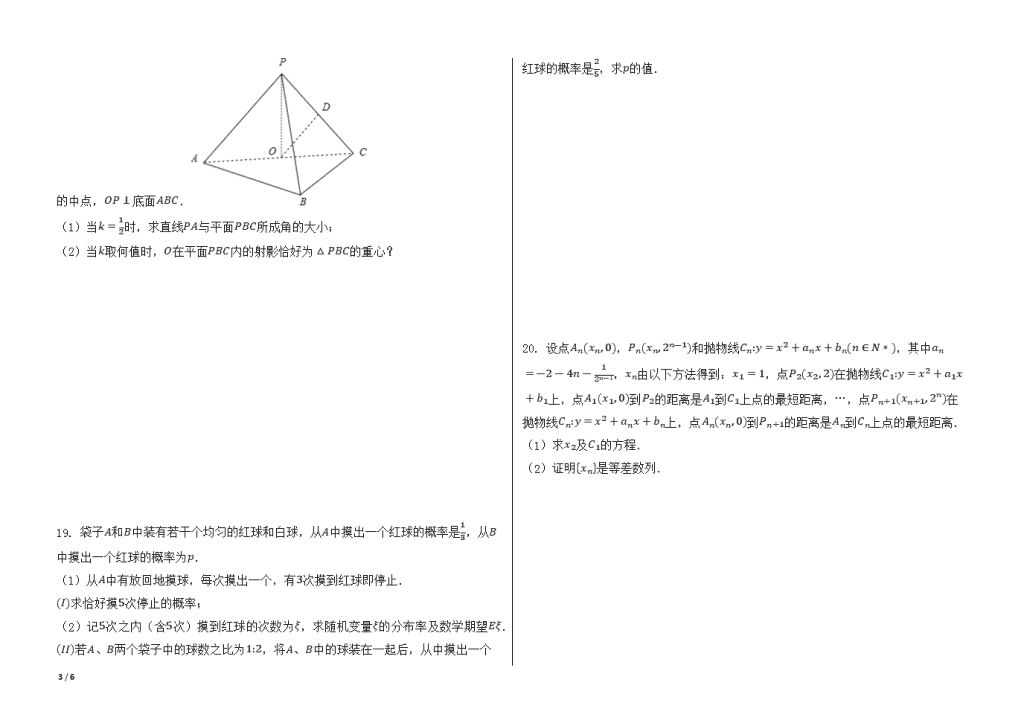
1 / 6 2005 年浙江省高考数学试卷（理科） 一、选择题（共 10 小题，每小题 5 分，满分 50 分） 1. lim 푛→∞ 1 + 2 + 3 + … + 푛 푛2 = ( ) A.2 B.4 C.1 2 D.0 2. 点(1,  ― 1)到直线푥 ― 푦 +1＝0的距离是（ ） A.1 2 B.3 2 C. 2 2 D.3 2 2 3. 设푓(푥) = {|푥 ― 1| ― 2，|푥| ≤ 1， 1 1 + 푥2，|푥| > 1， 则푓[푓(1 2)] = ( ) A.1 2 B. 4 13 C. ― 9 5 D.25 41 4. 在复平面内，复数 푖 1 + 푖 +(1 + 3푖)2对应的点位于（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 5. 在(1 ― 푥)5 +(1 ― 푥)6 +(1 ― 푥)7 +(1 ― 푥)8的展开式中，含푥3的项的系数是（ ） A.74 B.121 C. ― 74 D. ― 121 6. 设훼，훽为两个不同的平面，푙，푚为两条不同的直线，且푙 ⊂ 훼，푚 ⊂ 훽，有如下的 两个命题：①若훼 // 훽，则푙 // 푚；②若푙 ⊥ 푚，则훼 ⊥ 훽.那么（ ） A.①是真命题，②是假命题 B.①是假命题，②是真命题 C.①②都是真命题 D.①②都是假命题 7. 设集合퐴 = {(푥, 푦)|푥, 푦, 1 ― 푥 ― 푦是三角形的三边长}，则퐴所表示的平面区域（不 含边界的阴影部分）是( ) A. B. C. D. 8. 已知푘 < ―4，则函数푦 = cos2푥 + 푘(cos푥 ― 1)的最小值是（ ） A.1 B. ― 1 C.2푘 +1 D. ― 2푘 +1 9. 设푓(푛) = 2푛 +1(푛 ∈ 푁)，푃 = {1, 2, 3, 4, 5}，푄 = {3, 4, 5, 6, 7}，记푃 = {푛 ∈ 푁|푓(푛 ) ∈ 푃}，푄 = {푛 ∈ 푁|푓(푛) ∈ 푄}，则(푃 ∩ 퐶푁푄) ∪ (푄 ∩ 퐶푁푃) = ( ) A.{0, 3} B.{1, 2} C.{3, 4, 5} D.{1, 2, 6, 7} 10. 已知向量 → 푎 ≠ → 푒，| → 푒| = 1，对任意푡 ∈ 푅，恒有| → 푎 ― 푡 → 푒| ≥ | → 푎 ― → 푒|，则（ ） A. → 푎 ⊥ → 푒 B. → 푎 ⊥ ( → 푎 ― → 푒) C. → 푒 ⊥ ( → 푎 ― → 푒) D.( → 푎 + → 푒) ⊥ ( → 푎 ― → 푒) 二、填空题（共 4 小题，每小题 4 分，满分 16 分） 11. 函数푦 = 푥 푥 + 2(푥 ∈ 푅，且푥 ≠ ―2)的反函数是________． 12. 设푀、푁是直角梯形퐴퐵퐶퐷两腰的中点，퐷퐸 ⊥ 퐴퐵于퐸（如图）、现将 △ 퐴퐷퐸沿퐷퐸 折起，使二面角퐴 ― 퐷퐸 ― 퐵为45∘，此时点퐴在平面퐵퐶퐷퐸内的射影恰为点퐵，则푀、푁 的连线与퐴퐸所成角的大小等于________． 13. 过双曲线푥2 푎2 ― 푦2 푏2 = 1(푎 > 0, 푏 > 0)的左焦点且垂直于푥轴的直线与双曲线相交于푀、 푁两点，以푀푁为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于________． 2 / 6 14. 从集合{푂, 푃, 푄, 푅, 푆}与{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}中各任取2个元素排成一排（字母和 数字均不能重复）．每排中字母푂，푄和数字0至多只能出现一个的不同排法种数是 ________．（用数字作答）． 三、解答题（共 6 小题，每题 14 分，满分 84 分） 15. 已知函数푓(푥) = ― 3sin2푥 + sin푥cos푥． (퐼)求푓(25휋 6 )的值； (퐼퐼)设훼 ∈ (0, 휋)，푓(훼 2) = 1 4 ― 3 2 ，求sin훼的值． 16. 已知函数푓(푥)和푔(푥)的图象关于原点对称，且푓(푥) = 푥2 +2푥． （1）求函数푔(푥)的解析式； （2）解不等式푔(푥) ≥ 푓(푥) ― |푥 ― 1|． 17. 如图，已知椭圆的中心在坐标原点，焦点퐹1，퐹2在푥轴上，长轴퐴1퐴2的长为4，左 准线푙与푥轴的交点为푀，|푀퐴1|:|퐴1퐹1| = 2:1． （1）求椭圆的方程； （2）若直线푙1:푥 = 푚(|푚| > 1)，푃为푙1上的动点，使∠퐹1푃퐹2最大的点푃记为푄，求点푄 的坐标（用푚表示）． 18. 如图，在三棱锥푃 ― 퐴퐵퐶中，퐴퐵 ⊥ 퐵퐶，퐴퐵 = 퐵퐶 = 푘푃퐴，点푂、퐷分别是퐴퐶、푃퐶 3 / 6 的中点，푂푃 ⊥ 底面퐴퐵퐶． （1）当푘 = 1 2时，求直线푃퐴与平面푃퐵퐶所成角的大小； （2）当푘取何值时，푂在平面푃퐵퐶内的射影恰好为 △ 푃퐵퐶的重心？ 19. 袋子퐴和퐵中装有若干个均匀的红球和白球，从퐴中摸出一个红球的概率是1 3，从퐵 中摸出一个红球的概率为푝． （1）从퐴中有放回地摸球，每次摸出一个，有3次摸到红球即停止． (퐼)求恰好摸5次停止的概率； （2）记5次之内（含5次）摸到红球的次数为휉，求随机变量휉的分布率及数学期望퐸휉． (퐼퐼)若퐴、퐵两个袋子中的球数之比为1:2，将퐴、퐵中的球装在一起后，从中摸出一个 红球的概率是2 5，求푝的值． 20. 设点퐴푛(푥푛, 0)，푃푛(푥푛, 2푛―1)和抛物线퐶푛:푦 = 푥2 + 푎푛푥 + 푏푛(푛 ∈ 푁 ∗ )，其中푎푛 = ―2 ― 4푛 ― 1 2푛―1，푥푛由以下方法得到：푥1 = 1，点푃2(푥2, 2)在抛物线퐶1:푦 = 푥2 + 푎1푥 + 푏1上，点퐴1(푥1, 0)到푃2的距离是퐴1到퐶1上点的最短距离，…，点푃푛+1(푥푛+1, 2푛)在抛 物线퐶푛:푦 = 푥2 + 푎푛푥 + 푏푛上，点퐴푛(푥푛, 0)到푃푛+1的距离是퐴푛到퐶푛上点的最短距离． （1）求푥2及퐶1的方程． （2）证明{푥푛}是等差数列． 4 / 6 参考答案与试题解析 2005 年浙江省高考数学试卷（理科） 一、选择题（共 10 小题，每小题 5 分，满分 50 分） 1.C 2.D 3.B 4.B 5.D 6.D 7.A 8.A 9.A 10.C 二、填空题（共 4 小题，每小题 4 分，满分 16 分） 11.푦 = 2푥 1 ― 푥(푥 ∈ 푅，且푥 ≠ 1) 12.90∘ 13.2 14.8424 三、解答题（共 6 小题，每题 14 分，满分 84 分） 15.解：(1)∵ sin25휋 6 = 1 2，cos25휋 6 = 3 2 ，∴ 푓(25휋 6 ) = ― 3sin225휋 6 + sin25휋 6 cos25휋 6 = 0． (2)푓(푥) = 3 2 cos2푥 ― 3 2 + 1 2sin2푥． ∴ 푓(훼 2) = 3 2 cos훼 + 1 2sin훼 ― 3 2 = 1 4 ― 3 2 16sin2훼 ― 4sin훼 ― 11 = 0， 解得sin훼 = 1 ± 3 5 8 ∵ 훼 ∈ (0, 휋)，∴ sin훼 > 0 故sin훼 = 1 + 3 5 8 ． 16.解：（1）设函数푦 = 푓(푥)的图象上任意一点푄(푥0, 푦0)关于原点的对称点为푃(푥, 푦)， 则 {푥0 + 푥 2 = 0 푦0 + 푦 2 = 0 ，即{푥0 = ―푥 푦0 = ―푦． ∵ 点푄(푥0, 푦0)在函数푦 = 푓(푥)的图象上， ∴ ― 푦 = 푥2 ― 2푥，即푦 = ― 푥2 +2푥，∴ 푔(푥) = ― 푥2 +2푥． （2）由푔(푥) ≥ 푓(푥) ― |푥 ― 1|，可得2푥2 ― |푥 ― 1| ≤ 0． 当푥 ≥ 1时，2푥2 ― 푥 +1 ≤ 0，此时不等式无解； 当푥 < 1时，2푥2 + 푥 ― 1 ≤ 0，解得 ― 1 ≤ 푥 ≤ 1 2． ∴ 原不等式的解集为[ ―1,1 2]． 17.解：（1）设椭圆方程为푥2 푎2 + 푦2 푏2 = 1(푎 > 푏 > 0)，半焦距为푐，则|푀퐴1| = 푎2 푐 ― 푎，|퐴1 퐹1| = 푎 ― 푐． 由题意，得{푎2 푐 ― 푎 = 2(푎 ― 푐) 2푎 = 4 푎2 = 푏2 + 푐2 ∴ 푎 = 2，푏 = 3，푐 = 1．故椭圆方程为푥2 4 + 푦2 3 = 1． （2）设푃(푚, 푦0)，|푚| > 1， 当푦0 = 0时，∠퐹1푃퐹2 = 0； 当푦0 ≠ 0时，0 < ∠퐹1푃퐹2 < 푃퐹1푀 < 휋 2， ∴ 只需求tan∠퐹2푃퐹2的最大值即可． 设直线푃퐹1的斜率푘1 = 푦0 푚 + 1，直线푃퐹2的斜率푘2 = 푦0 푚 ― 1， ∴ tan∠퐹1푃퐹2 = | 푘2 ― 푘1 1 + 푘1푘2 | = 2|푦0| 푚2 ― 1 + 푦20 ≤ 2|푦0| 2 푚2 ― 1 ⋅ |푦0| = 1 푚2 ― 1 当且仅当 푚2 ― 1 = |푦0|时，∠퐹1푃퐹2最大，∴ 푄(푚,  ± 푚2 ― 1)|푚| > 1． 18.解：方法一：（1）∵ 퐴퐵 ⊥ 퐵퐶，푂퐴 = 푂퐶，∴ 푂퐴 = 푂퐵 = 푂퐶，又∵ 푂푃 5 / 6 ⊥ 平面퐴퐵퐶，∴ 푃퐴 = 푃퐵 = 푃퐶．取퐵퐶中点퐸，连接푃퐸，则퐵퐶 ⊥ 平面푃푂퐸作푂퐹 ⊥ 푃퐸于퐹，连接퐷퐹，则푂퐹 ⊥ 平面푃퐵퐶∴ ∠푂퐷퐹是푂퐷与平面푃퐵퐶所成的角． 又푂퐷 // 푃퐴，∴ 푃퐴与平面푃퐵퐶所成的角的大小等于∠푂퐷퐹，在푅푡 △ 푂퐷퐺中，sin∠ 푂퐷퐹 = 푂퐹 푂퐷 = 210 30 ， ∴ 푃퐴与平面푃퐵퐶所成角为arcsin 210 30 ． （2）由（1）知，푂퐹 ⊥ 平面푃퐵퐶，∴ 퐹是푂在平面푃퐵퐶内的射影． ∵ 퐷是푃퐶的中点， 若点퐹是 △ 푃퐵퐶的重心，则퐵，퐹，퐷三点共线， ∴ 直线푂퐵在平面푃퐵퐶内的射影为直线퐵퐷，∵ 푂퐵 ⊥ 푃퐶，∴ 푃퐶 ⊥ 퐵퐷，∴ 푃퐵 = 퐵퐶，即푘 = 1． 反之，当푘 = 1时，三棱锥푂 ― 푃퐵퐶为正三棱锥， ∴ 푂在平面푃퐵퐶内的射影为 △ 푃퐵퐶的重心． 方法二：∵ 푂푃 ⊥ 平面퐴퐵퐶，푂퐴 = 푂퐶，퐴퐵 = 퐵퐶，∴ 푂퐴 ⊥ 푂퐵，푂퐴 ⊥ 푂푃，푂퐵 ⊥ 푂푃． 以푂为原点，射线푂푃为非负푧轴，建立空间直角坐标系푂 ― 푥푦푧（如图）． 设퐴퐵 = 푎，则퐴( 2 2 푎, 0, 0)，퐵(0,  2 2 푎, 0)，퐶( ― 2 2 푎, 0, 0)， 设푂푃 = ℎ，则푃(0, 0, ℎ) （1）∵ 푘 = 1 2，即푃퐴 = 2푎，∴ ℎ = 7 2푎，∴ → 푃퐴 = ( 2 2 푎, 0,  ― 7 2푎)， 可求得平面푃퐵퐶的法向量 → 푛 = (1． ― 1,  ― 1 7)，∴ cos < → 푃퐴， → 푛 >= ˙ | → 푃퐴| ⋅ | → 푛| = 210 30 ， 设푃퐴与平面푃퐵퐶所成的角为휃，则sin휃 = cos < → 푃퐴， → 푛 >= 210 30 ， (2) △ 푃퐵퐶的重心퐺( ― 2 6 푎,  2 6 푎, 1 3ℎ)，∴ → 푂퐺 = ( ― 2 6 푎,  2 6 푎, 1 3ℎ)， ∵ 푂퐺 ⊥ 平面푃퐵퐶，∴ → 푂퐺 ⊥ → 푃퐵， 又 → 푃퐵 = (0,  2 2 푎,  ― ℎ)，∴ → 푂퐺 ⋅ → 푃퐵 = 1 6푎2 ― 1 3ℎ2 = 0，∴ 푃퐴 = 푂퐴2 + ℎ2 = 푎，即푘 = 1， 反之，当푘 = 1时，三棱锥푂 ― 푃퐵퐶为正三棱锥． ∴ 푂在平面푃퐵퐶内的射影为 △ 푃퐵퐶的重心． 19.解：(1)(퐼)由题意知本题是在相同的条件下进行的试验，且事件发生的概率相同， 可以看作独立重复试验，恰好摸5次停止表示第五次一定摸到红球，前四次有两次摸 到红球，根据独立重复试验公式得到 휉 0 1 2 3 푃 32 243 80 243 80 243 17 243 퐶24 × (1 3)2 × (2 3)2 × 1 3 = 8 81． （2）由题意知从퐴中有放回地摸球，每次摸出一个，有3次摸到红球即停止 6 / 6 ∴ 随机变量휉的取值为0，1，2，3； 由푛次独立重复试验概率公式푃푛(푘) = 퐶푘푛푝푘(1 ― 푝)푛―푘，得 푃(휉 = 0) = 퐶05 × (1 ― 1 3)5 = 32 243； 푃(휉 = 1) = 퐶15 × 1 3 × (1 ― 1 3)4 = 80 243； 푃(휉 = 2) = 퐶25 × (1 3)2 × (1 ― 1 3)3 = 80 243； 푃(휉 = 3) = 퐶33(1 3)3 + 퐶23 ⋅ (1 3)2 ⋅ 2 3 ⋅ 1 3 + 퐶24(1 3)2(2 3)2 ⋅ 1 3 = 17 81． 随机变量휉的分布列是 ∴ 휉的数学期望是퐸휉 = 32 243 × 0 + 80 243 × 1 + 80 243 × 2 + 51 243 × 3 = 131 81 ． （2）由题意知本题是一个古典概型， 设袋子퐴中有푚个球，则袋子퐵中有2푚个球． 试验发生的所有事件是3푚， 而满足条件的是1 3푚 +2푚푝， 根据古典概型公式得到 1 3푚 + 2푚푝 3푚 = 2 5， ∴ 푝 = 13 30． 20.解：（1）由题意得퐴1(1, 0)，퐶1:푦 = 푥2 ― 7푥 + 푏1， 设点푃(푥, 푦)是퐶1上任意一点， 则|퐴1푃| = (푥 ― 1)2 + 푦2 = (푥 ― 1)2 + (푥2 ― 7푥 + 푏1)2 令푓(푥) = (푥 ― 1)2 +(푥2 ― 7푥 + 푏1)2 则푓′(푥) = 2(푥 ― 1) + 2(푥2 ― 7푥 + 푏1)(2푥 ― 7) 由题意得푓′(푥2) = 0， 即2(푥2 ― 1) + 2(푥22 ― 7푥 + 푏1)(2푥2 ― 7) = 0 又푃2(푥2, 2)在퐶1上，∴ 2 = 푥22 ― 7푥2 + 푏1 解得푥2 = 3，푏1 = 14 故퐶1的方程为푦 = 푥2 ― 7푥 +14 （2）设点푃(푥, 푦)是퐶푛上任意一点， 则|퐴푛푃| = (푥 ― 푥푛)2 + 푦2 = (푥 ― 푥푛)2 + (푥2 + 푎푛푥 + 푏푛)2 令푔(푥) = (푥 ― 푥푛)2 +(푥2 + 푎푛푥 + 푏푛)2 则푔′(푥) = 2(푥 ― 푥푛) + 2(푥2 + 푎푛푥 + 푏푛)(2푥 + 푎푛) 由题意得푔′(푥푛+1) = 0 即2(푥푛+1 ― 푥푛) + 2(푥2푛+1 + 푎푛푥 + 푏푛)(2푥푛+1 + 푎푛) = 0 又∵ 2푛 = 푥푛+1，∴ (푥푛+1 ― 푥푛) + 2푛(2푥푛+1 + 푎푛) = 0(푛 ≥ 1)， 即(1 + 2푛+1)푥푛+1 ― 푥푛 + 2푛푎푛 = 0( ∗ ) 下面用数学归纳法证明푥푛 = 2푛 ― 1， ①当푛 = 1时，푥1 = 1，等式成立； ②假设当푛 = 푘时，等式成立，即푥푘 = 2푘 ― 1， 则当푛 = 푘 +1时，由( ∗ )知(1 + 2푘+1)푥푘+1 ― 푥푘 + 2푘푎푘 = 0， 又푎푘 = 2 ― 4푘 ― 1 2푘―1，∴ 푥푘+1 = 푥푘 ― 2푘푎푘 1 + 2푘+1 = 2푘 +1， 即푛 = 푘 +1时，等式成立． 由①②知，等式对푛 ∈ 푁∗成立， 故{푥푛}是等差数列．