2020届高考文科数学二轮专题复习课件：专题6 概率与统计2-6-解答题 2

2020届高考文科数学二轮专题复习课件：专题6 概率与统计2-6-解答题 2

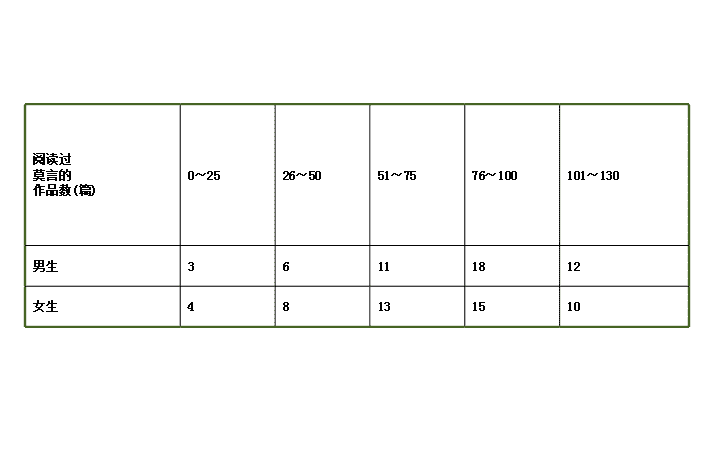
第 2 课时　　 概率与统计案例的综合应用 考向一　概率与独立性检验 【例 1 】 大家知道 , 莫言是中国首位获得诺贝尔奖的文学家 , 国人欢欣鼓舞 . 某高校文学社从男女生中各抽取 50 名同学调查他们对莫言作品的了解程度 , 结果如下 : 阅读过 莫言的 作品数 ( 篇 ) 0 ～ 25 26 ～ 50 51 ～ 75 76 ～ 100 101 ～ 130 男生 3 6 11 18 12 女生 4 8 13 15 10 (1) 试估计该校学生阅读莫言作品 超过 50 篇的概率 . ① (2) 对莫言作品阅读超过 75 篇的则称为“对莫言作品非常了解” , 否则为“一般了解” . 根据题意完成下表 , 并 判断能否有 75% 的把握 ② 认为对莫言作品非常了解与性别有关 ? 非常了解 一般了解 总计 男生 女生 总计 附 :K 2 = 【题眼直击 】 题眼 思维导引 ① 想到利用古典概型概率公式求概率 ② 想到利用 K 2 的计算公式求解 【解析 】 (1) 由抽样调查得阅读莫言作品在 50 篇以上的 频率为 , 据此估计该校学生阅 读莫言作品超过 50 篇的概率约为 . (2) 非常了解 一般了解 总计 男生 30 20 50 女生 25 25 50 总计 55 45 100 根据列联表数据得 K 2 的观测值 k= ≈1.010<1.323, 所以没有 75% 的把握认为对莫言作品非 常了解与性别有关 . 【拓展提升 】 　独立性检验的步骤 (1) 根据样本数据制成 2×2 列联表 . (2) 计算 K 2 的观测值 k. (3) 比较临界值的大小关系作统计判断 . 　 【变式训练】　 国内某知名大学有男生 14 000 人 , 女生 10 000 人 , 该校体育学院想了解本校学生的运动状况 , 根据性别采取分层抽样的方法从全校学生中抽取 120 人 , 统计他们平均每天运动的时间 , 如表 .( 平均每天运动的时间单位 : 小时 , 该校学生平均每天运动的时间范围是 [0,3]) 男生平均每天运动的时间分布情况 : 平均每天 运动的时间 [0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5) [2.5,3] 人数 2 12 23 18 10 x 女生平均每天运动的时间分布情况 : 平均每天 运动的时间 [0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5) [2.5,3] 人数 5 12 18 10 3 y (1) 请根据样本估算该校男生平均每天运动的时间 ( 结果精确到 0.1). (2) 若规定平均每天运动的时间不少于 2 小时的学生为“运动达人” , 低于 2 小时的学生为“非运动达人” . ① 请根据样本估算该校“运动达人”的数量 ; ② 请根据上述表格中的统计数据填写下面 2×2 列联表 , 并通过计算判断能否在犯错误的概率不超过 0.05 的前提下认为“运动达人”与性别有关 ? 运动达人 非运动达人 总计 男生 女生 总计 参考公式 :K 2 = , 其中 n=a+b+c+d . 参考数据 : P(K 2 ≥k 0 ) 0.10 0.05 0.025 k 0 2.706 3.841 5.024 【解析 】 (1) 由分层抽样可知 , 抽取的男生人数为 120× =70, 抽取的女生人数为 120-70=50, 故 x=5,y=2. 则该校男生平均每天运动的时间为 : ≈1.5, 故该校男生平均每天运动的时间约为 1.5 小时 . (2)① 样本中“运动达人”所占比例是 , 故估计 该校“运动达人”有 ×(14 000+10 000)= 4 000( 人 ). ② 完成 2×2 列联表如下 : 运动达人 非运动达人 总计 男生 15 55 70 女生 5 45 50 总计 20 100 120 由列联表可得 K 2 的观测值 k= ≈2.743<3.841, 所以不能在犯错误的概率不超过 0.05 的前提下认为 “运动达人”与性别有关 . 考向二　概率与回归分析 【例 2 】 随着人民生活水平的日益提高 , 某小区居民拥有私家车的数量与日俱增 . 由于该小区建成时间较早 , 没有配套建造地下停车场 , 小区内无序停放的车辆造成了交通的拥堵 . 该小区的物业公司统计了近五年小区登 记在册的私家车数量 ( 累计值 , 如 124 表示 2016 年小区登记在册的所有车辆数 , 其余意义相同 ), 得到如下数据 : 编号 x 1 2 3 4 5 年份 2014 2015 2016 2017 2018 数量 y( 单位 : 辆 ) 34 95 124 181 216 (1) 若私家车的数量 y 与编号 x 满足 线性相关关系 ① , 求 y 关于 x 的线性回归方程 , 并预测 2020 年该小区的私家车数量 . (2) 小区于 2018 年底完成了基础设施改造 , 划设了 120 个 停车位 . 为解决小区车辆乱停乱放的问题 , 加强小区管 理 , 物业公司决定禁止无车位的车辆进入小区 . 由于车 位有限 , 物业公司决定在 2019 年度采用网络竞拍的方式 将车位对业主出租 , 租期一年 , 竞拍方案如下 :① 截至 2018 年已登记在册的私家车业主拥有竞拍资格 ;② 每车 至多申请一个车位 , 由车主在竞拍网站上提出申请并给 出自己的报价 ;③ 根据物价部门的规定 , 竞价不得超过 1 200 元 ;④ 申请阶段截止后 , 将所有申请的业主报价自 高到低排列 , 排在前 120 位的业主以其报价成交 ;⑤ 若最 后出现并列的报价 , 则以提出申请的时间在前的业主成交 . 为预测本次竞拍的成交最低价 , 物业公司随机抽取了有竞拍资格的 40 位业主进行竞拍意向的调查 , 统计了他们的拟报竞价 , 得到如下频率分布直方图 : 世纪金榜导学号 (i) 求所抽取的业主中有意向竞拍报价不低于 1 000 元的人数 ; (ii) 如果所有符合条件的车主均参与竞拍 , 利用 样本估 计总体的思想 ② , 请你据此预测至少需要报价多少元才 能竞拍车位成功 ?( 精确到整数 ). 参考公式 : 对于一组数据 (x 1 ,y 1 ),(x 2 ,y 2 ), … ,(x n ,y n ), 其回归方程 的斜率和截距的最小二乘估计 分别为 : 【题眼直击 】 题眼 思维导引 ① 想到利用最小二乘法求线性回归方程 ② 想到结合频率分布直方图 , 利用样本估计总体 【解析 】 (1) 由表中数据 , 计算得 , ×(1+2+3+4+5)=3, ×(34+95+124+181+216)=130, =45, =130-45×3=-5, 故所求线性回归方程为 =45x-5, 令 x=7, 得 =310, 所以预测 2020 年该小区的私家车数量为 310 辆 . (2)(i) 由频率分布直方图可知 , 有意向竞拍报价不低于 1 000 元的频率为 (0.25+0.05)×1=0.3, 共抽取 40 位业主 , 则 40×0.3=12, 所以有意向竞拍报价不低于 1 000 元的人数为 12 人 . (ii) 由题意 , , 所以竞价自高到低排列位于前 比例的业主可以竞拍 成功 , 结合频率分布直方图 , 预测竞拍成功的最低报价为 1 000- ×100= ≈974( 元 ). 【拓展提升 】 　求回归直线方程的步骤 (1) 依据样本数据画出散点图 , 确定两个变量具有线性 相关关系 ( 有时可省略 ). (2) 计算出 的值 . (3) 计算回归系数 . (4) 写出回归直线方程 . 【变式训练 】 假设关于某设备的使用年限 x( 年 ) 和所支出的维修费用 y( 万元 ) 有如下表的统计资料 : 使用年限 x/( 年 ) 2 3 4 5 6 维修费用 y/( 万元 ) 2.2 3.8 5.5 6.5 7.0 若由资料可知 y 对 x 呈线性相关关系 , 试求 : (1) 线性回归方程 . (2) 根据线性回归方程 , 估计使用年限为 12 年时 , 维修费用是多少 ? 【解析 】 (1) 列表 i 1 2 3 4 5 总计 x i 2 3 4 5 6 20 y i 2.2 3.8 5.5 6.5 7.0 25 x i y i 4.4 11.4 22.0 32.5 42.0 112.3 4 9 16 25 36 90 = 于是 = - =5-1.23×4=0.08. 所以线性回归方程为 =1.23x+0.08. (2) 当 x=12 时 , =1.23×12+0.08=14.84( 万元 ), 即估计使用 12 年时 , 维修费用是 14.84 万元 .