【数学】2020届天津一轮复习通用版1-1 集合的概念及运算作业
专题一 集合与常用逻辑用语
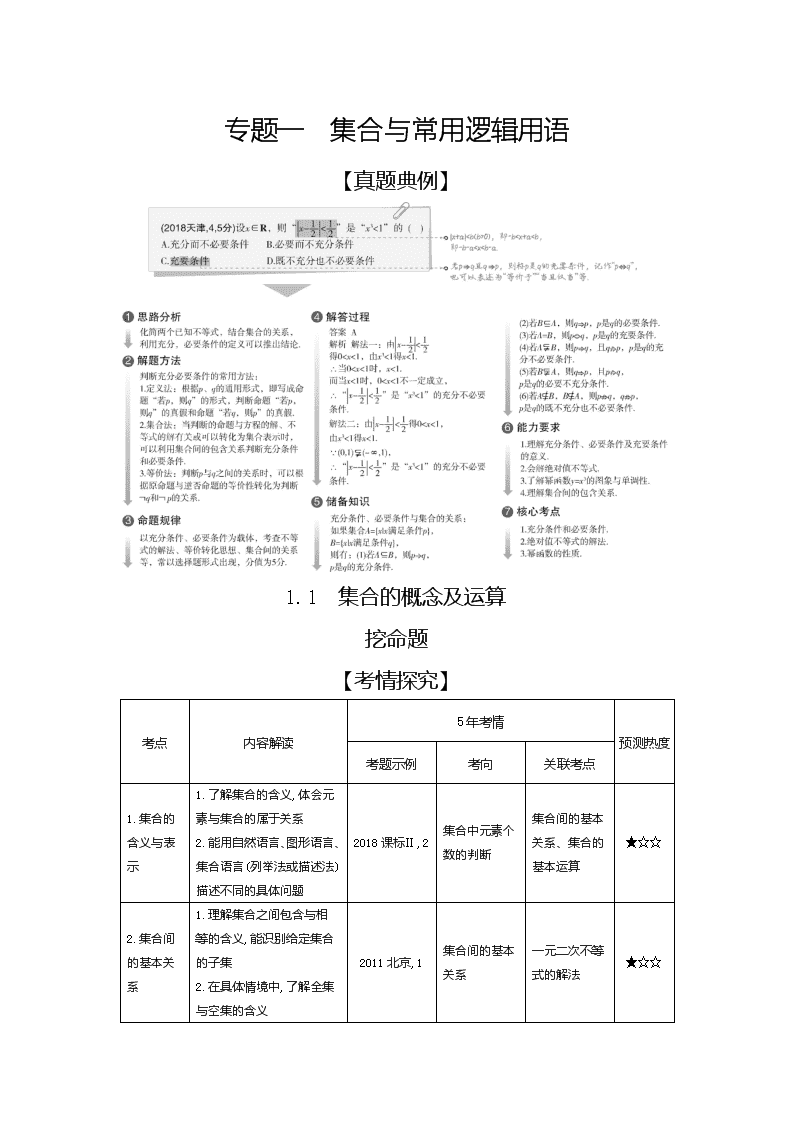
【真题典例】
1.1 集合的概念及运算
挖命题
【考情探究】
考点
内容解读
5年考情
预测热度
考题示例
考向
关联考点
1.集合的含义与表示
1.了解集合的含义,体会元素与集合的属于关系
2.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题
2018课标Ⅱ,2
集合中元素个数的判断
集合间的基本关系、集合的基本运算
★☆☆
2.集合间的基本关系
1.理解集合之间包含与相等的含义,能识别给定集合的子集
2.在具体情境中,了解全集与空集的含义
2011北京,1
集合间的基本关系
一元二次不等式的解法
★☆☆
3.集合的基本运算
1.理解两个集合的并集与交集的含义,
2018天津,1
2018天津文,1
集合的交、并、补运算
不等式和方程的解法
★★★
会求两个简单集合的并集与交集
2.理解在给定集合中一个子集的补集的含义,会求给定子集的补集
3.能使用韦恩(Venn)图表示集合间的关系及运算
2017天津,1
2016天津,1
分析解读 1.掌握集合的表示方法,能判断元素与集合的属于关系、集合与集合之间的包含关系.
2.深刻理解、掌握交、并、补集的概念,熟练掌握集合的交、并、补的运算和性质,能用韦恩(Venn)图表示集合的关系及运算.
3.本部分内容在高考试题中多以选择题的形式出现,以函数、不等式等知识为载体,以集合语言和符号语言为表现形式,考查数学思想方法.
4.本节内容在高考中分值约为5分,属中低档题.
破考点
【考点集训】
考点一 集合的含义与表示
1.(2018课标Ⅱ,2,5分)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
答案 A
2.(2012课标全国,1,5分)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所含元素的个数为( )
A.3 B.6 C.8 D.10
答案 D
考点二 集合间的基本关系
3.已知集合A={0,a},B={x|-1
2},则A∩B=( )
A.{x|-32} C.{x|21} D.A∩B=⌀
答案 A
3.(2017课标Ⅲ,1,5分)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为( )
A.3 B.2 C.1 D.0
答案 B
4.(2017课标Ⅱ,2,5分)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A.{1,-3} B.{1,0} C.{1,3} D.{1,5}
答案 C
5.(2016课标Ⅰ,1,5分)设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )
A.-3,-32 B.-3,32 C.1,32 D.32,3
答案 D
6.(2016课标Ⅱ,2,5分)已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=( )
A.{1} B.{1,2} C.{0,1,2,3} D.{-1,0,1,2,3}
答案 C
7.(2015课标Ⅱ,1,5分)已知集合A={-2,-1,0,1,2},B={x|(x-1)(x+2)<0},则A∩B=( )
A.{-1,0} B.{0,1} C.{-1,0,1} D.{0,1,2}
答案 A
8.(2014课标Ⅱ,1,5分)设集合M={0,1,2},N={x|x2-3x+2≤0},则M∩N=( )
A.{1} B.{2} C.{0,1} D.{1,2}
答案 D
9.(2014课标Ⅰ,1,5分)已知集合A={x|x2-2x-3≥0},B={x|-2≤x<2},则A∩B=( )
A.[-2,-1] B.[-1,2) C.[-1,1] D.[1,2)
答案 A
10.(2018北京,20,14分)设n为正整数,集合A={α|α=(t1,t2,…,tn),tk∈{0,1},k=1,2,…,n}.对于集合A中的任意元素α=(x1,x2,…,xn)和β=(y1,y2,…,yn),记
M(α,β)=12[(x1+y1-|x1-y1|)+(x2+y2-|x2-y2|)+…+(xn+yn-|xn-yn|)].
(1)当n=3时,若α=(1,1,0),β=(0,1,1),求M(α,α)和M(α,β)的值;
(2)当n=4时,设B是A的子集,且满足:对于B中的任意元素α,β,当α,β相同时,M(α,β)是奇数;当α,β不同时,M(α,β)是偶数.求集合B中元素个数的最大值;
(3)给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素α,β,M(α,β)=0.写出一个集合B,使其元素个数最多,并说明理由.
解析 (1)因为α=(1,1,0),β=(0,1,1),
所以M(α,α)=12[(1+1-|1-1|)+(1+1-|1-1|)+(0+0-|0-0|)]=2,
M(α,β)=12[(1+0-|1-0|)+(1+1-|1-1|)+(0+1-|0-1|)]=1.
(2)设α=(x1,x2,x3,x4)∈B,则M(α,α)=x1+x2+x3+x4.
由题意知x1,x2,x3,x4∈{0,1},且M(α,α)为奇数,
所以x1,x2,x3,x4中1的个数为1或3.所以
B⊆{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);(0,1,0,0),(1,1,0,1);(0,0,1,0),(1,0,1,1);(0,0,0,1),(0,1,1,1).
经验证,对于每组中两个元素α,β,均有M(α,β)=1.
所以每组中的两个元素不可能同时是集合B的元素.
所以集合B中元素的个数不超过4.
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,
所以集合B中元素个数的最大值为4.
(3)设Sk={(x1,x2,…,xn)|(x1,x2,…,xn)∈A,xk=1,x1=x2=…=xk-1=0}(k=1,2,…,n),
Sn+1={(x1,x2,…,xn)|x1=x2=…=xn=0},
所以A=S1∪S2∪…∪Sn+1.
对于Sk(k=1,2,…,n-1)中的不同元素α,β,
经验证,M(α,β)≥1.
所以Sk(k=1,2,…,n-1)中的两个元素不可能同时是集合B的元素.
所以B中元素的个数不超过n+1.
取ek=(x1,x2,…,xn)∈Sk且xk+1=…=xn=0(k=1,2,…,n-1).
令B={e1,e2,…,en-1}∪Sn∪Sn+1,则集合B的元素个数为n+1,且满足条件.
故B是一个满足条件且元素个数最多的集合.
C组 教师专用题组
1.(2018北京,1,5分)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )
A.{0,1} B.{-1,0,1} C.{-2,0,1,2} D.{-1,0,1,2}
答案 A
2.(2017北京,1,5分)若集合A={x|-23},则A∩B=( )
A.{x|-2
查看更多