2020_2021学年新教材高中数学第三章函数概念与性质3
第
1
课时 函数的单调性
必备知识
·
自主学习
1.
函数的单调性
(1)
定义
导思
1.
怎样描述函数的图象上升、下降的性质?
2.
什么是函数的单调区间?
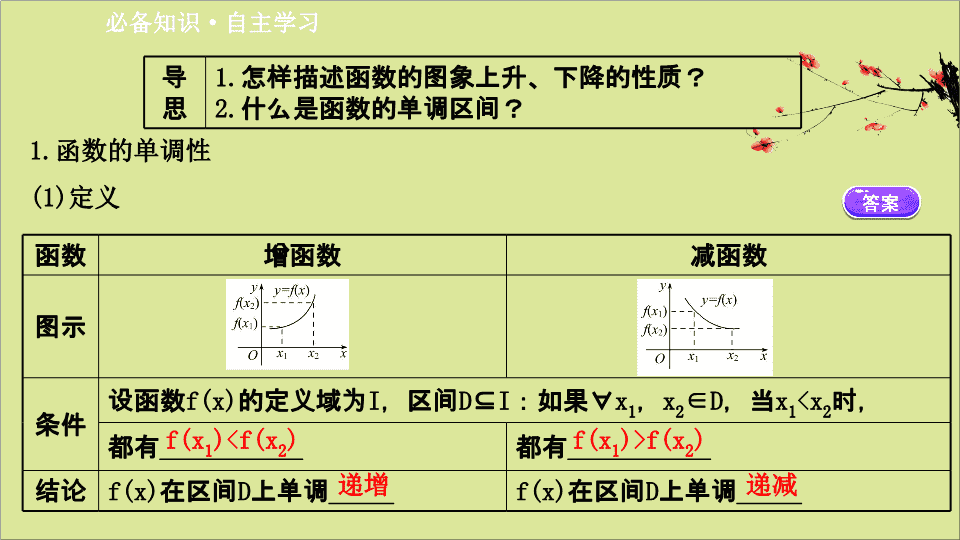
函数
增函数
减函数
图示
条件
设函数
f(x)
的定义域为
I
,区间
D⊆I
:如果∀
x
1
,
x
2
∈D
,当
x
1
f(x
2
)
递增
递减
(2)
本质:函数的单调性反映的是两个变量的对应变换规律,定量地刻画了函数在区间上图象的变化趋势,是函数诸多性质中最核心、最本质的性质
.
(3)
应用:证明函数的单调性、比较大小、解不等式、求参数范围等
.
【
思考
】
函数单调性的定义中,能否将“∀”改为“∃”?
提示:
不能,一些特殊的值满足并不能说明函数的单调性
.
2.
单调函数与函数的单调性
(1)
单调函数:当函数在它的定义域上单调递增
(
减
)
时,就称它是增
(
减
)
函
数;
(2)
单调性与单调区间:如果函数
y=f(x)
在区间
D
上单调递增或单调递减,那么
就说函数
y=f(x)
在这一区间具有
(
严格的
)_______
,区间
D
叫做
y=f(x)
的
_____
_____.
单调性
单调
区间
【
思考
】
函数
y=f(x)
在定义域内的每一个区间
D
1
,
D
2
,
…
上都单调递减,那么函数在定
义域上是减函数吗?你能举例说明吗?
提示:
不是
.
如函数
y=
在
(-∞
,
0)
,
(0
,
+∞)
上都单调递减,但在定义域上
不具有单调性
.
【
基础小测
】
1.
辨析记忆
(
对的打“√”,错的打“
×”)
(1)
函数
f(x)=x
2
,因为
-1<2
,且
f(-1)f(x
2
)⇨
函数在
(2
,
+∞)
上单调递减
四步
内容
书写
表达
因为
20
,
所以
f(x
1
)-f(x
2
)>0
,即
f(x
1
)>f(x
2
).
所以函数
f(x)=
在
(2
,
+∞)
上单调递减
.
注意书写的规范性:
①
x
1
,
x
2
取值任意且分大小;②变形是解题关键
.
题后
反思
利用定义法证明函数单调性的关键是作差之后的变形,且变形的结果是几个因式乘积的形式
.
【
解题策略
】
利用定义证明函数单调性的步骤
【
题组训练
】
(2020·
哈尔滨高一检测
)
求证:函数
f(x)=- -1
在区间
(-∞
,
0)
上单调递增
.
【
证明
】
∀x
1
,
x
2
∈(-∞
,
0)
,且
x
1
0
,
所以
f(x
1
)-f(x
2
)<0
,即
f(x
1
)0
时,函数
y=
与
y=f(x)
的单调性相反,对于
f(x)<0
也成立
.
(2)
在公共定义域内,两增函数的和仍为增函数,增函数减去一个减函数所得的函数为增函数
.
(3)
函数
f(x)
与
f(x)+c(c
为常数
)
具有相同的单调性
.
(4)
当
c>0
时,函数
f(x)
与
cf(x)
具有相同的单调性;
当
c<0
时,函数
f(x)
与
cf(x)
具有相反的单调性
.
2.
函数
y=x+ (a≠0)
的单调性
(1)
若
a>0
,函数
y=x+
的图象如图
1
所示,
则函数
y=x+
的单调增区间是
(-∞
,
- ]
和
[
,
+∞)
,单调减区间是
(-
,
0)
和
(0
,
).
(2)
若
a<0
,其图象如图
2
所示,
函数
y=x+
在
(-∞
,
0)
和
(0
,
+∞)
上均单调递增,即
y=x+
的单调增区间
为
(-∞
,
0)
和
(0
,
+∞).
【
拓展训练
】
(2020·
杭州高一检测
)
函数
y=2x+
的单调递增区间为
_______.
【
解析
】
y=2
,由对勾函数的图象可知,
单调递增区间为
(-∞
,
- )
和
(
,
+∞).
答案:
(-∞
,
- )
和
(
,
+∞)
类型三 函数单调性的简单应用
(
数学抽象、逻辑推理
)
角度
1
利用单调性解不等式
【
典例
】
(2020·
佛山高一检测
)
函数
f(x)
在
[0
,
+∞)
上单调递减,且
f(2)=
-1
,则满足
f(2x-4)>-1
的实数
x
的取值范围是
(
)
A.(3
,
+∞) B.(-∞
,
3)
C.[2
,
3) D.[0
,
3)
【
思路导引
】
从定义域,单调性两个方面列不等式求范围
.
【
解析
】
选
C.
因为
f(2)=-1
,
所以由
f(2x-4)>-1
得,
f(2x-4)>f(2)
,
且
f(x)
在
[0
,
+∞)
上单调递减,
所以
0≤2x-4<2
,解得
2≤x<3
,
所以满足
f(2x-4)>-1
的实数
x
的取值范围是
[2
,
3).
【
变式探究
】
本例的条件若改为“单调递增”,试求
x
的取值范围
.
【
解析
】
因为
f(2)=-1
,
所以由
f(2x-4)>-1
,得
f(2x-4)>f(2)
,
又
f(x)
在
[0
,
+∞)
上单调递增,
所以
2x-4>2
,解得
x>3.
角度
2
分段函数的单调性
【
典例
】
(2020·
宜春高一检测
)
已知函数
f(x)=
是增函数,则实数
a
的取值范围是
_______.
【
思路导引
】
分别考查
x≥1
,
x<1
,分界点三个方面的因素求范围
.
【
解析
】
因为函数
f(x)=
在
(-∞
,
+∞)
上单调递增,
又函数
y= ax
2
-ax-1
的对称轴为
x=1
,
所以 解得
- ≤a<0.
答案:
【
解题策略
】
1.
解抽象函数不等式问题的方法
利用函数的单调性解不等式主要依据函数单调性的定义和性质,将符号“
f ”
脱掉,列出关于未知量的不等式
(
组
)
,然后求解,要注意函数的定义域
.
2.
分段函数的单调性
首先分析每段上的单调性,其次是分界点处函数值的大小,如果是增函数,则分界点左侧值小于等于右侧值,如果是减函数,则分界点左侧值大于等于右侧值
.
【
题组训练
】
1.(2020·
沈阳高一检测
)f(x)=x|x|
,若
f(2m+1)+f(1-m)>0
,则
m
的取值范围是
(
)
A.(-∞
,
-1) B.(-∞
,
-2)
C.(-1
,
+∞) D.(-2
,
+∞)
【
解析
】
选
D.
因为
f(x)=x|x|=
所以
f(x)
在
R
上是增函数,且
f(-x)=-f(x)
,
所以由
f(2m+1)+f(1-m)>0
得,
f(2m+1)>f(m-1)
,所以
2m+1>m-1
,解得
m>-2
,
所以
m
的取值范围为
(-2
,
+∞).
2.
定义域在
R
上的函数
f(x)
满足对任意的
x
1
,
x
2
∈R
,且
x
1
≠x
2
,都有
(x
1
-x
2
)[f(x
1
)-f(x
2
)]>0
,则有
(
)
A.f(-2)0
,
当
x
1
x
2
时,
x
1
-x
2
>0
,则
f(x
1
)-f(x
2
)>0
,即
f(x
1
)>f(x
2
).
可得函数
f(x)
是在
R
上的增函数,
所以
f(-2)0
时,恒有
f(x)>1.
(1)
求证:
f(x)
是增函数
.
(2)
若
f(3)=4
,解不等式
f(a
2
+a-5)<2.
【
思路导引
】
(1)
按照单调性的定义,构造
f(x
2
)-f(x
1
)
,再判断符号
.
(2)
将
2
化为
f(x
0
)
的形式,再利用单调性解不等式
.
【
解析
】
(1)
设
x
1
,
x
2
∈R
,且
x
1
0
,
所以
f(x
2
-x
1
)>1
,
f(x
2
)-f(x
1
)=f((x
2
-x
1
)+x
1
)-f(x
1
)
=f(x
2
-x
1
)+f(x
1
)-1-f(x
1
)>0
,
即
f(x
2
)>f(x
1
)
,所以
f(x)
是
R
上的增函数
.
(2)
因为
m
,
n∈R
,不妨设
m=n=1
,
所以
f(1+1)=f(1)+f(1)-1
,即
f(2)=2f(1)-1
,
f(3)=f(2+1)=f(2)+f(1)-1=2f(1)-1+f(1)-1=3f(1)-2=4
,所以
f(1)=2.
所以
f(a
2
+a-5)0
,满足
f( )=f(x)-f(y).
(1)
证明函数
f(x)
是增函数
.
(2)
若
f(6)=1
,解不等式
f(x+3)-f( )<2.
【
解析
】
(1)
因为当
01 D.k<1
【
解析
】
选
D.k-1>0
时,
由
y=
可知,在区间
(-∞
,
0)
,
(0
,
+∞)
上单调递减,不合题意;
当
k-1<0
时,由
y=
可知,在区间
(-∞
,
0)
,
(0
,
+∞)
上单调递增,故
k<1.
4.
若
f(x)
是减函数,且
f(3x-2)3
,
解得
x> .
答案:
5.
函数
f(x)=2x
2
-3|x|
的单调递增区间是
_______.
【
解析
】
函数
f(x)=2x
2
-3|x|=
的图象如图所示,
故它的单调递增区间为
答案: