- 2021-06-30 发布 |
- 37.5 KB |
- 6页
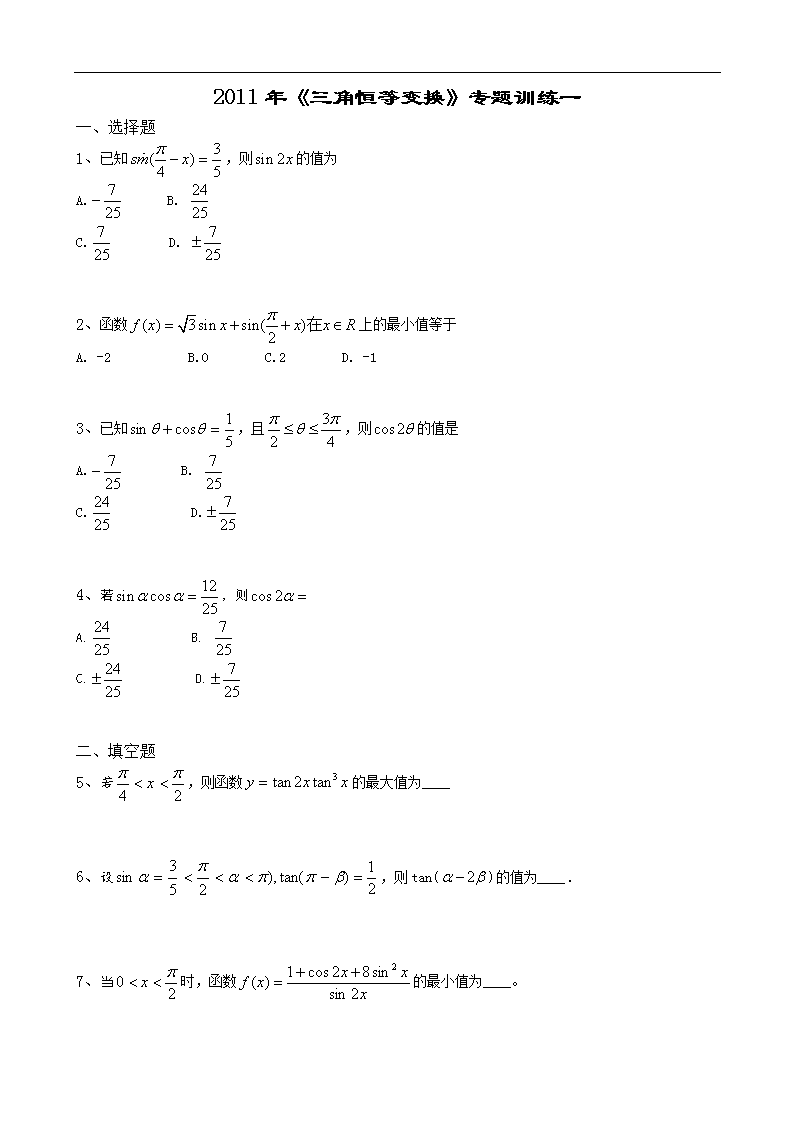


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011高考数学专题复习:《三角恒等变换》专题训练一
2011年《三角恒等变换》专题训练一 一、选择题 1、已知,则的值为 A. B. C. D. 2、函数上的最小值等于 A. -2 B.O C.2 D. -1 3、已知,且,则的值是 A. B. C. D. 4、若,则 A. B. C. D. 二、填空题 5、若,则函数的最大值为____ 6、设,则tan()的值为____. 7、当时,函数的最小值为____。 8、若,则=____. 9、如果.且,那么____. 10、已知函数,又,若的最小值为,则正数的值为____. 三、解答题 11、如图13 -1,,是单位圆O上的点,,分别是圆0与轴的两个交点,△为正三角形. (1)若点的坐标为求的值; (2)若,四边形的周长为,试将表示成的函数,并求出的最大值. 12、在△ABC中,,,分别是角,,的对边,,且//. (1)求角的大小; (2)求的值域. 13、已知锐角△ABC中,三个内角为,,,两向量 ,若与是共线向量. (1)求角的大小; (2)求函数取最大值时角的大小. 14、已知向量 (1)求的值; (2)若,且,求的值. 15、已知.且 (1)求的值; (2)求. 以下是答案 一、选择题 1、 解析 2、A 解析 由于, 故其最小值为-2。 3、解析。由于 即。又 ,于是 4、 解析: 二、填空题 5、-8 解析 6、 解析 由。得 ,故于是 7、4解析 当且仅当,即时,取=。 存在x.使,这时. 8、 解析 所以,因此 9、 解析 10、 解析 又由.且的最小值为.可知,于是 三、解答题 11、(1)设,由已知得, 12、(1)由得由正弦定理,得 由(1)得 13、 化简得, △ABC为锐角三角形, ,当B =60。时函数取得最大值2. 14、 解得 由,得由,得 15、(1)由 (2)由叉 由得,查看更多