2020届艺术生高考数学二轮复习课时训练：第二章 函数、导数及其应用 第8节

2020届艺术生高考数学二轮复习课时训练：第二章 函数、导数及其应用 第8节

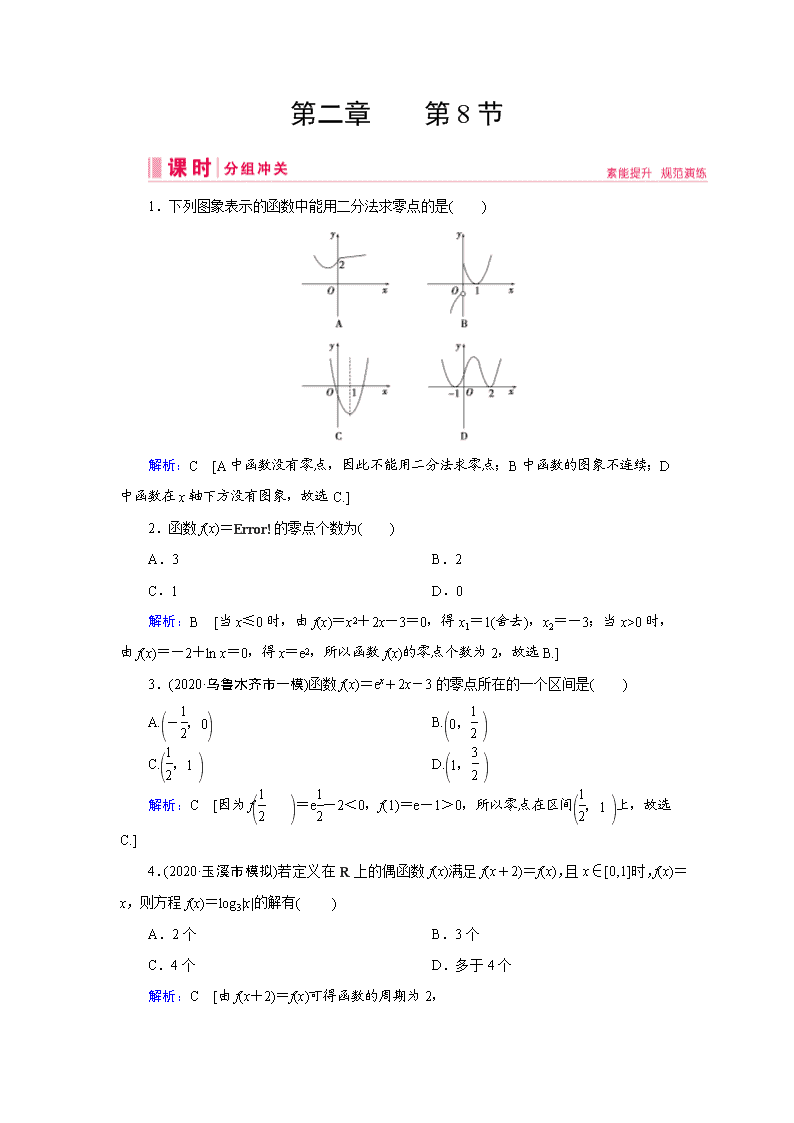
第二章 第8节 ‎1．下列图象表示的函数中能用二分法求零点的是(　　)‎ 解析：C　[A中函数没有零点，因此不能用二分法求零点；B中函数的图象不连续；D中函数在x轴下方没有图象，故选C.]‎ ‎2．函数f(x)＝的零点个数为(　　)‎ A．3　　　　　　　　　　 B．2 ‎ C．1 D．0‎ 解析：B　[当x≤0时，由f(x)＝x2＋2x－3＝0，得x1＝1(舍去)，x2＝－3；当x>0时，由f(x)＝－2＋ln x＝0，得x＝e2，所以函数f(x)的零点个数为2，故选B.]‎ ‎3．(2020·乌鲁木齐市一模)函数f(x)＝ex＋2x－3的零点所在的一个区间是(　　)‎ A. B. C. D. 解析：C　[因为f＝e－2＜0，f(1)＝e－1＞0，所以零点在区间上，故选C.]‎ ‎4．(2020·玉溪市模拟)若定义在R上的偶函数f(x)满足f(x＋2)＝f(x)，且x∈[0,1]时，f(x)＝x，则方程f(x)＝log3|x|的解有(　　 )‎ A．2个 B．3个 C．4个 D．多于4个 解析：C　[由f(x＋2)＝f(x)可得函数的周期为2，‎ 又函数为偶函数且当x∈[0,1]时，f(x)＝x，‎ 故可作出函数f(x)的图象．‎ ‎∴方程f(x)＝log3|x|的解个数等价于y＝f(x)与y＝log3|x|图象的交点个数，‎ 由图象可得它们有4个交点，故方程f(x)＝log3|x|的解的个数为4，故选C.]‎ ‎5．(2020·西宁市模拟)定义在R上的偶函数f(x)满足f(x＋1)＝－f(x)，当x∈[0,1]时，f(x)＝－2x＋1，设函数g(x)＝|x－1|(－1＜x＜3)，则函数f(x)与g(x)的图象所有交点的横坐标之和为(　　 )‎ A．2 B．4‎ C．6 D．8‎ 解析：B　[∵f(x＋1)＝－f(x)，‎ ‎∴f(x＋2)＝－f(x＋1)＝f(x)，‎ ‎∴f(x)的周期为2.‎ ‎∴f(1－x)＝f(x－1)＝f(x＋1)，‎ 故f(x)的图象关于直线x＝1对称．‎ 又g(x)＝|x－1|(－1＜x＜3)的图象关于直线x＝1对称，作出f(x)和g(x)的函数图象如图所示：‎ 由图象可知两函数图象在(－1,3)上共有4个交点，‎ ‎∴所有交点的横坐标之和为2×2＝4.故选B.]‎ ‎6．已知函数f(x)＝＋a的零点为1，则实数a的值为　________　.‎ 解析：由已知得f(1)＝0，即＋a＝0，‎ 解得a＝－.‎ 答案：－ ‎7．已知函数f(x)＝logax＋x－b(a>0，且a≠1)．当21，－1<3－b<0，‎ ‎∴f(3)>0，即f(2)f(3)<0，故x0∈(2,3)，即n＝2.‎ 答案：2‎ ‎8．已知函数f(x)＝则函数g(x)＝f(x)－的零点所构成的集合为　________　.‎ 解析：令g(x)＝0，得f(x)＝，所以或解得x＝－1或x＝或x＝，故函数g(x)＝f(x)－的零点所构成的集合为.‎ 答案： ‎9．设函数f(x)＝ax2＋bx＋b－1(a≠0)．‎ ‎(1)当a＝1，b＝－2时，求函数f(x)的零点；‎ ‎(2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．‎ 解：(1)当a＝1，b＝－2时，f(x)＝x2－2x－3，‎ 令f(x)＝0，得x＝3或x＝－1.‎ ‎∴函数f(x)的零点为3或－1.‎ ‎(2)依题意，f(x)＝ax2＋bx＋b－1＝0有两个不同实根，‎ ‎∴b2－‎4a(b－1)>0恒成立，‎ 即对于任意b∈R，b2－4ab＋‎4a>0恒成立，‎ 所以有(－‎4a)2－4×(‎4a)<0⇒a2－a<0，解得00)．‎ ‎(1)作出函数f(x)的图象；‎ ‎(2)当0

查看更多