【数学】2020届一轮复习人教B版（理）第十二章60几何概型作业

【数学】2020届一轮复习人教B版（理）第十二章60几何概型作业

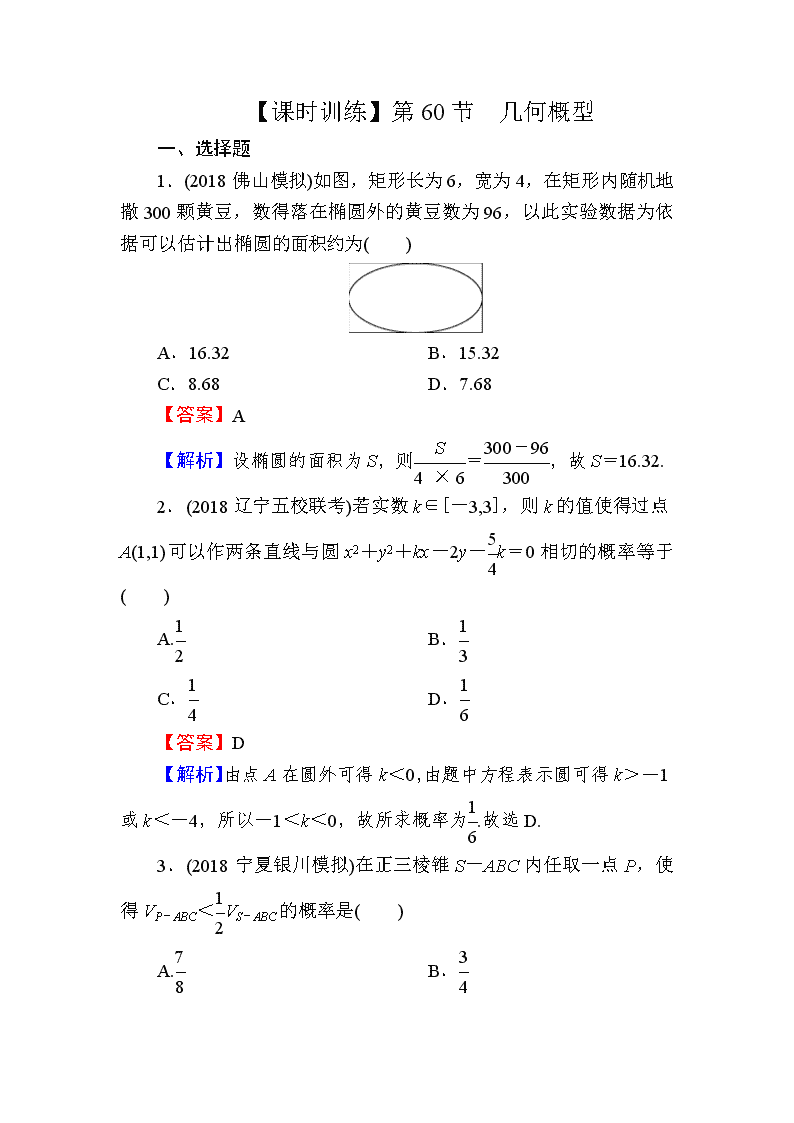
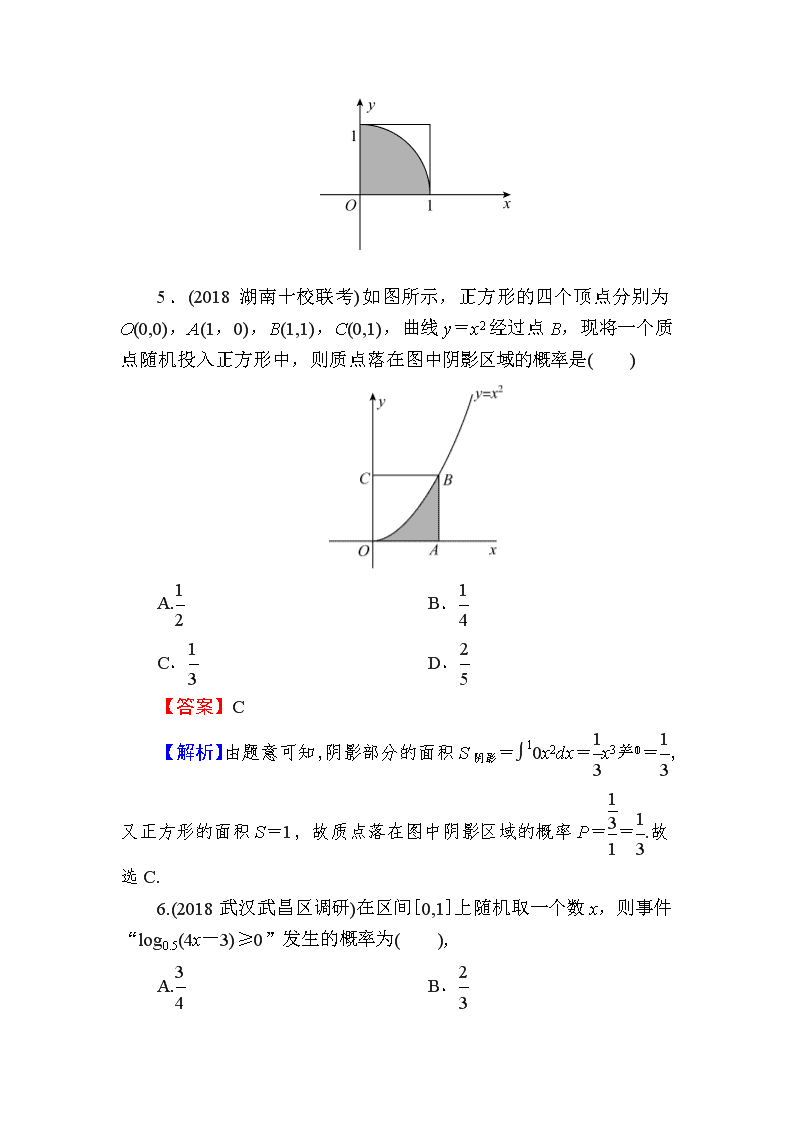
【课时训练】第 60 节　几何概型 一、选择题 1．(2018 佛山模拟)如图，矩形长为 6，宽为 4，在矩形内随机地 撒 300 颗黄豆，数得落在椭圆外的黄豆数为 96，以此实验数据为依 据可以估计出椭圆的面积约为(　　) A．16.32 B．15.32 C．8.68 D．7.68 【答案】A 【解析】设椭圆的面积为 S，则 S 4 × 6 ＝300－96 300 ，故 S＝16.32. 2．(2018 辽宁五校联考)若实数 k∈[－3,3]，则 k 的值使得过点 A(1,1)可以作两条直线与圆 x2＋y2＋kx－2y－ 5 4 k＝0 相切的概率等于 (　　) A.1 2 B．1 3 C．1 4 D．1 6 【答案】D 【解析】由点 A 在圆外可得 k＜0，由题中方程表示圆可得 k＞－ 1 或 k＜－4，所以－1＜k＜0，故所求概率为1 6 .故选 D. 3．(2018 宁夏银川模拟)在正三棱锥 S－ABC 内任取一点 P，使 得 VP－ABC＜1 2 VS－ABC 的概率是(　　) A.7 8 B．3 4 C．1 2 D．1 4 【答案】A 【解析】如图，分别取 D，E，F 为 SA，SB，SC 的中点，则满 足条件的点 P 应在棱台 DEF－ABC 内，而 S△DEF＝1 4 S△ABC，∴VS－DEF ＝1 8 VS－ABC. ∴P＝VDEF－ABC VS－ABC ＝7 8 .故选 A. 4．(2018 石家庄一模)在区间[0,1]上随意选择两个实数 x，y，则 使 x2＋y2≤1 成立的概率为(　　) A.π 2 B．π 4 C．π 3 D．π 5 【答案】B 【解析】如图所示，试验的全部结果构成正方形区域，使得 x2＋y2≤1 成立的平面区域为以坐标原点 O 为圆心，1 为半径的圆 的1 4 与 x 轴正半轴，y 轴正半轴围成的区域，由几何概型的概率计算公 式得，所求概率 P＝ π 4 1 ＝π 4 .故选 B. 5．(2018 湖南十校联考)如图所示，正方形的四个顶点分别为 O(0,0)，A(1，0)，B(1,1)，C(0,1)，曲线 y＝x2 经过点 B，现将一个质 点随机投入正方形中，则质点落在图中阴影区域的概率是(　　) A.1 2 　 B．1 4 C．1 3 D．2 5 【答案】C 【解析】由题意可知，阴影部分的面积 S阴影＝∫10x2dx＝1 3 x310＝ 1 3 ，又正方形的面积 S＝1，故质点落在图中阴影区域的概率 P＝ 1 3 1 ＝1 3 . 故选 C. 6.(2018 武汉武昌区调研)在区间[0,1]上随机取一个数 x，则事件 “log0.5(4x－3)≥0”发生的概率为(　　), A.3 4 B．2 3 C．1 3 D．1 4 , 【答案】D,【解析】因为 log0.5(4x－3)≥0，所以 0＜4x－3≤1， 即3 4 ＜x≤1，所以所求概率 P＝ 1－3 4 1－0 ＝1 4 .故选 D., 7．(2018 济南模拟)如图所示，在边长为 1 的正方形 OABC 内任 取一点 P(x，y)，则以 x，y,1 为边长能构成锐角三角形的概率为 (　　), A.1－π 4 B．1－π 6 C.1－π 3 D． π 12 【答案】A,【解析】连接 AC，首先由 x＋y＞1 得构成三角形的 点 P 在△ABC 内，若构成锐角三角形，则最大边 1 所对的角 α 必是 锐角，cos α＝x2＋y2－12 2xy ＞0，x2＋y2＞1，即点 P 在以原点为圆心，1 为半径的圆外．∴点 P 在边 AB，BC 及圆弧 AC 围成的区域内．∴所 求概率为 12－π 4 × 12 12 ＝1－π 4 .故选 A. 二、填空题 8.(2018 重庆检测)在不等式组Error!所表示的平面区域内随机 地取一点 P，则点 P 恰好落在第二象限的概率为________． 【答案】2 9 【解析】画出不等式组Error!表示的平面区域(如图中阴影部分 所示)，因为 S△ABC＝1 2 ×3×3 2 ＝9 4 ，S△AOD＝1 2 ×1×1＝1 2 ，所以点 P 恰 好落在第二象限的概率为S △ AOD S △ ABC ＝ 1 2 9 4 ＝2 9 . 9．(2018 邢台摸底考试)有一个底面半径为 1，高为 3 的圆柱， 点 O1，O2 分别为这个圆柱上底面和下底面的圆心，在这个圆柱内随 机 取 一 点 P ， 则 点 P 到 点 O1 ， O2 的 距 离 都 大 于 1 的 概 率 为 ________． 【答案】5 9 【解析】由题意知，所求的概率为 1－(4π 3 × 13)÷(π×12×3)＝ 5 9 . 10．(2018 沈阳模拟)某人家门前挂了两盏灯笼，这两盏灯笼发光 的时刻相互独立，且都在通电后的 5 秒内任意时刻等可能发生，则它 们通电后发光的时刻相差不超过 3 秒的概率是________． 【答案】21 25 【解析】设两盏灯笼通电后发光的时刻分别为 x，y，则由题意可 知 0≤x≤5,0≤y≤5，它们通电后发光的时刻相差不超过 3 秒，即|x－ y|≤3，做出图形如图所示，根据几何概型的概率计算公式可知，它们 通电后发光的时刻相差不超过 3 秒的概率 P＝1－ 2 × 1 2 × 2 × 2 5 × 5 ＝21 25 . 11．(2018 河南检测)若 m∈(0,3)，则直线(m＋2)x＋(3－m)y－3＝ 0 与 x 轴，y 轴围成的三角形的面积小于9 8 的概率为________． 【答案】2 3 【解析】对于直线方程(m＋2)x＋(3－m)y－3＝0，令 x＝0，得 y＝ 3 3－m ；令 y＝0，得 x＝ 3 m＋2 .由题意可得1 2 ·| 3 m＋2|·| 3 3－m|＜9 8 ，因为 m∈(0,3)，所以解得 0＜m＜2，由几何概型的概率计算公式可得，所 求事件的概率是2 3 . 12．(2018 云南昆明统测)在底和高等长度的锐角三角形中有一个 内接矩形 ABCD，矩形的一边 BC 在三角形的底边上，如图，在三角 形内任取一点，则该点取自矩形内的最大概率为________． 【答案】1 2 【解析】设 AD＝x，AB＝y，则由三角形相似可得x a ＝a－y a ，解得 y＝a－x，所以矩形的面积 S＝xy＝x(a－x)≤(x＋a－x 2 )2＝a2 4 ，当且仅 当 x＝a－x，即 x＝a 2 时，S 取得最大值a2 4 ，所以该点取自矩形内的最 大概率为 a2 4 1 2 × a × a ＝1 2 . 三、解答题 13．(2018 山东德州一模)设关于 x 的一元二次方程 x2＋2ax＋b2＝ 0.若 a 是从区间[0,3]任取的一个数，b 是从区间[0,2]任取的一个数， 求方程有实根的概率． 【解】设事件 A 为“方程 x2＋2ax＋b2＝0 有实根”．当 a≥0，b≥0 时，方程 x2＋2ax＋b2＝0 有实根的充要条件为 a≥b.试验的全部结果 所构成的区域为{(a，b)|0≤a≤3,0≤b≤2}，构成事件 A 的区域为{(a， b)|0≤a≤3,0≤b≤2，a≥b}，根据条件画出构成的区域(略)，可得所 求的概率为 P(A)＝ 3 × 2－1 2 × 22 3 × 2 ＝2 3 .