【数学】2020届一轮复习人教版(理)第7章第7讲立体几何中的向量方法作业
A组 基础关
1.如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )
A. B.
C. D.
答案 A
解析 不妨设CB=1,则B(0,0,1),A(2,0,0),C1(0,2,0),B1(0,2,1),∴=(0,2,-1),=(-2,2,1).cos〈,〉===.∴直线BC1与直线AB1夹角的余弦值为.
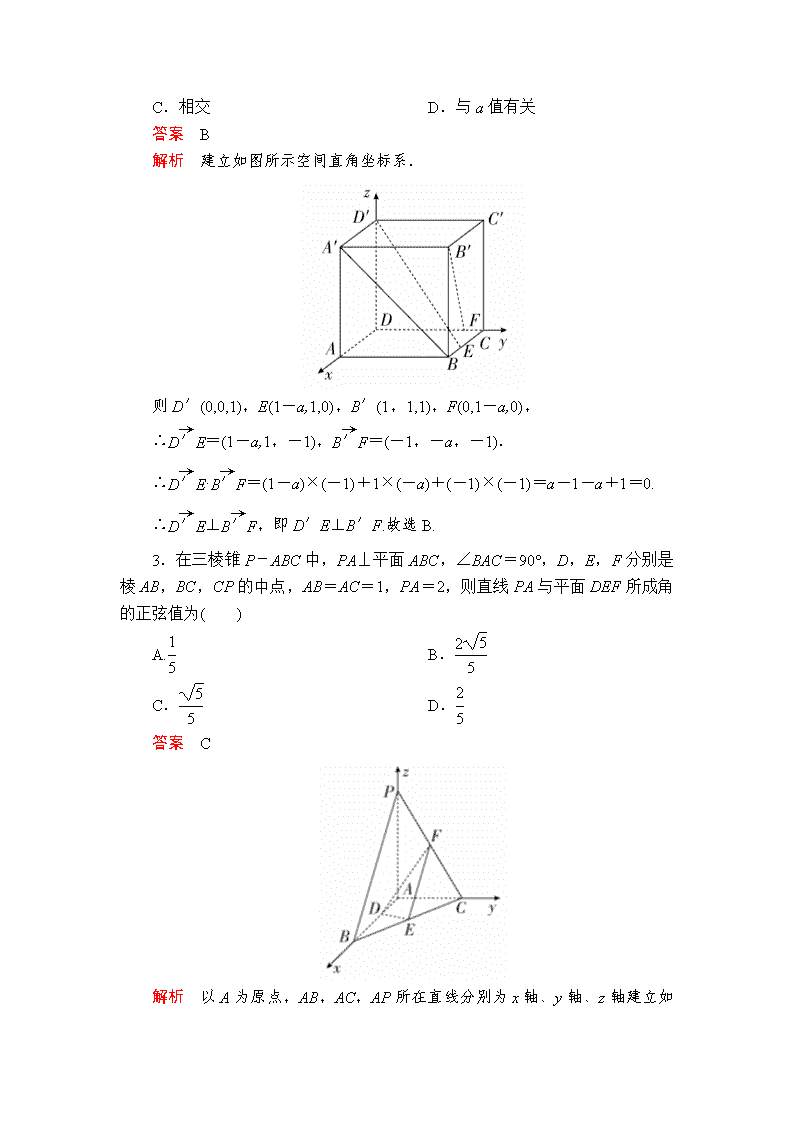
2.(2018·沧州模拟)如图所示,在正方体ABCD-A′B′C′D′中,棱长为1,E,F分别是BC,CD上的点,且BE=CF=a(0
0),则C(m,,0),A=(m,,0).
设n1=(x,y,z)为平面ACE的法向量,则即可取n1=.易知n2=(1,0,0)为平面DAE的一个法向量,由题设知|cos〈n1,n2〉|=,即=,解得m=.因为E为PD的中点,所以三棱锥E-ACD的高为.所以三棱锥E-ACD的体积V=××××=.
3.(2017·全国卷Ⅲ)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
答案 ②③
解析 依题意建立如图所示的空间直角坐标系.设等腰直角三角形ABC的直角边长为1.
由题意知点B在平面xOy中形成的轨迹是以C为圆心,1为半径的圆.
设直线a的方向向量为a=(0,1,0),直线b的方向向量为b=(1,0,0),以Ox轴为始边沿逆时针方向旋转的旋转角为θ,θ∈[0,2π),则B(cosθ,sinθ,0),
∴=(cosθ,sinθ,-1),||=.
设直线AB与a所成夹角为α,
则cosα==|sinθ|∈,
∴45°≤α≤90°,∴③正确,④错误.
设直线AB与b所成夹角为β,
则cosβ==|cosθ|.
当直线AB与a的夹角为60°,
即α=60°时,
则|sinθ|=cosα=cos60°=,
∴|cosθ|=.∴cosβ=|cosθ|=.
∵0°≤β≤90°,∴β=60°,即直线AB与b的夹角为60°.
∴②正确,①错误.
4.如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.已知BC=8,PO=4,AO=3,OD=2.
(1)证明:AP⊥BC;
(2)若点M是线段AP上一点,且AM=3.试证明平面AMC⊥平面BMC.
证明 如图所示,以O为坐标原点,以射线OP为z轴的正半轴建立空间直角坐标系Oxyz.则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0),P(0,0,4).
(1)∵=(0,3,4),=(-8,0,0),
∴·=(0,3,4)·(-8,0,0)=0,⊥,即AP⊥BC.
(2)由(1)知|AP|=5,
又|AM|=3,且点M在线段AP上,
∴==.
又=(-4,5,0),=(-4,-5,0),
∴=+=,
则A·B=(0,3,4)·=0,
∴⊥,即AP⊥BM,
又根据(1)的结论知AP⊥BC,BM∩BC=B,
∴AP⊥平面BMC,于是AM⊥平面BMC.
又AM⊂平面AMC,故平面AMC⊥平面BCM.
C组 素养关
1.在如图所示的多面体中,四边形ABCD是平行四边形,四边形BDEF是矩形,ED⊥平面ABCD,∠ABD=,AB=2AD.
(1)求证:平面BDEF⊥平面ADE;
(2)若ED=BD,求直线AF与平面AEC所成角的正弦值.
解 (1)证明:在△ABD中,
由正弦定理知=,
所以sin∠ADB===1,
所以∠ADB=90°,即BD⊥AD.
因为DE⊥平面ABCD,BD⊂平面ABCD,所以DE⊥BD.
又AD∩DE=D,所以BD⊥平面ADE.
因为BD⊂平面BDEF,所以平面BDEF⊥平面ADE.
(2)由(1)可得,在Rt△ABD中,∠BAD=,BD=AD,又由ED=BD,设AD=1,则BD=ED=.因为DE⊥平面ABCD,BD⊥AD,
所以可以点D为坐标原点,DA,DB,DE所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
则A(1,0,0),C(-1,,0),E(0,0,),F(0,,),
所以=(-1,0,),=(-2,,0).
设平面AEC的法向量为n=(x,y,z),则
即
令z=1,得n=(,2,1)为平面AEC的一个法向量.
因为=(-1,,),
所以cos〈n,〉==,
所以直线AF与平面AEC所成角的正弦值为.
2.如图,球O内接四面体ABCD,AB为球O的直径,平面BCD截球得圆O′,BD为圆O′的直径,C为圆O′上一点,AD⊥平面BCD,AD=2,BD=2,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(1)证明:PQ∥平面BCD;
(2)若二面角C-BM-D的大小为60°,求∠BDC的大小.
解 (1)证明:连接PO′,由中位线易知PO′∥AD,从而PO′⊥平面BCD.
如图,以O′为原点,O′D,O′P所在射线分别为y轴、z轴的正半轴,建立空间直角坐标系O′xyz.
由题意知A(0,,2),B(0,-,0),D(0,,0).
设点C的坐标为(x0,y0,0),因为=3,
所以Q.
因为M为AD的中点,故M(0,,1).
又P为BM的中点,
故P,所以=.
又平面BCD的一个法向量为u=(0,0,1),·u=0,
PQ⊄平面BCD,所以PQ∥平面BCD.
(2)设m=(x,y,z)为平面BMC的一个法向量.
由=(-x0,-y0,1),=(0,2,1),
可知
取y=-1,得m=.
又平面BDM的一个法向量为n=(1,0,0),于是
|cos〈m,n〉|===,
即2=3.①
又BC⊥CD,所以·=0,故(-x0,--y0,0)·(-x0,-y0,0)=0,即x+y=2.②
联立①②,结合点C在圆O′上且|y0|<,
解得
所以=,=,||=,||=,
所以tan∠BDC==.
又∠BDC是锐角,所以∠BDC=60°.