人教A高中数学必修三程序框图与算法的基本逻辑结构二导学案

人教A高中数学必修三程序框图与算法的基本逻辑结构二导学案

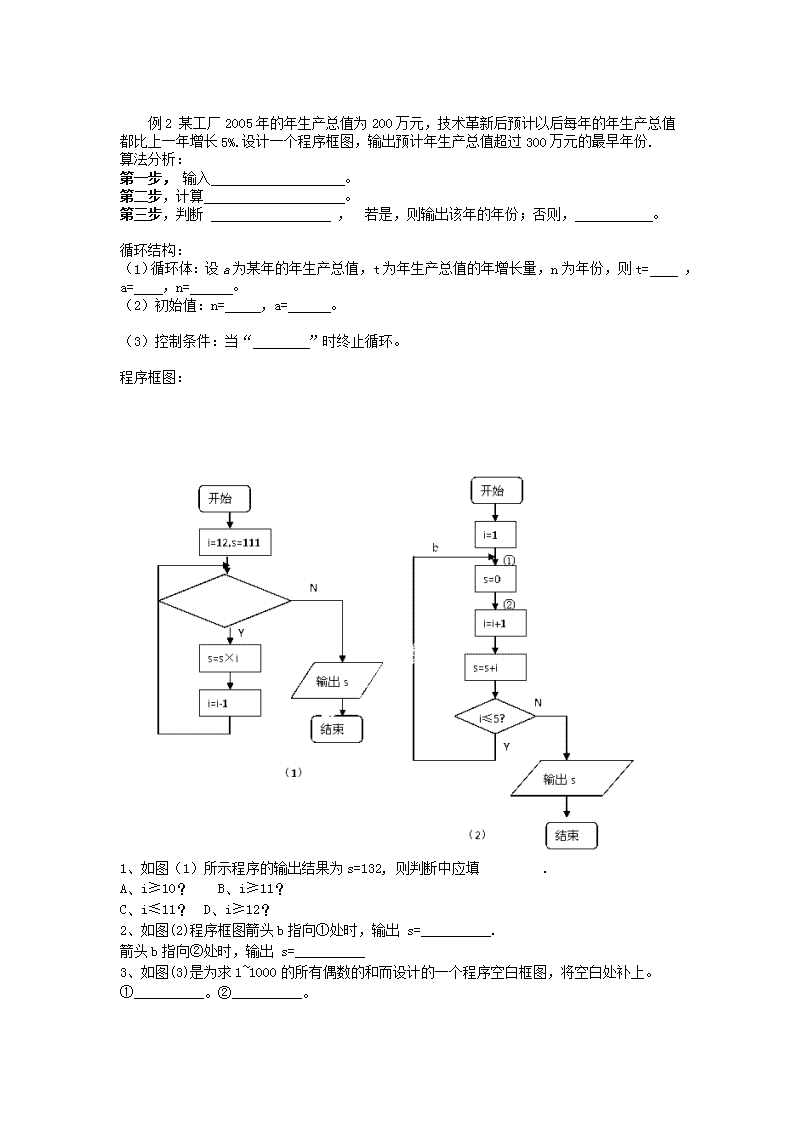
‎《‎1.1.2‎ 程序框图与算法的基本逻辑结构（二）》导学案 学习目标 ‎ ‎1、更进一步理解算法，‎ ‎2、掌握算法的条件结构和循环结构，‎ ‎3、掌握画程序框图的基本规则，能正确画出程序框图.学会灵活、正确地画程序框图。‎ 问题探究 知识探究（一）：算法的条件结构 思考1:在某些问题的算法中，有些步骤只有在一定条件下才会被执行，算法的流程因条件是否成立而变化.在算法的程序框图中，由若干个在一定条件下才会被执行的步骤组成的逻辑结构，称为 ，用程序框图可以表示为下面两种形式：‎ 你如何理解这两种程序框图的共性和个性？ ‎ 思考2:判断“以任意给定的3个正实数为三条边边长的三角形是否存在”的算法步骤如何设计？‎ 第一步，‎ 第二步， ‎ 思考3:你能画出这个算法的程序框图吗？ ‎ 知识探究（二）：算法的循环结构 思考1:在算法的程序框图中，由按照一定的条件反复执行的某些步骤组成的逻辑结构，称为 ，反复执行的步骤称为 ，那么循环结构中一定包含条件结构吗？ ‎ 思考2: 直到型循环结构用程序框图可以表示为： ‎ 你能指出直到型循环结构的特征吗？ ‎ 在 后，对条件进行判断，如果 ，就 ，直到 时终止循环。‎ 思考3:当型循环结构用程序框图可以表示为：‎ 你能指出当型循环结构的特征吗？‎ 在 前，对条件进行判断，如果 ，就 ，否则终止循环。‎ 思考4:计算1+2+3+…+100的值可按如下过程进行：‎ 第1步，0+1=1.‎ 第2步，1+2=3.‎ 第3步，3+3=6.‎ 第4步，6+4=10.‎ ‎ ……‎ 第100步，4950+100=5050. ‎ 我们用一个 变量S表示每一步的计算结果，即把S+i的结果仍记为S，从而把第i步表示为 ，其中S的初始值为 ，i依次取1，2，…，100，通过重复操作，上述问题的算法如何设计？‎ 第一步，令i=1，S=0.‎ 第二步，‎ 第三步， ‎ 第四步，‎ 思考5:用直到型循环结构和当型循环结构，程序框图中判断的条件分别为： ‎ i = i + 1‎ Sum=Sum + i i = i + 1‎ Sum=Sum + i 是 否 否 是 理论迁移 例1 设计一个求解一元二次方程ax2+bx+c=0的算法，并画出程序框图表示. ‎ 算法分析：‎ 第一步，输入三个系数a，b，c。‎ 第二步，计算 。‎ 第三步，判断 是否成立.若是，则计算 ；否则，输出“方程没有实数根”，结束算法。‎ 第四步，判断 是否成立。若是，则输出 ，否则，计算 ，并输出 。‎ 程序框图：‎ 例2 某工厂2005年的年生产总值为200万元，技术革新后预计以后每年的年生产总值都比上一年增长5%.设计一个程序框图，输出预计年生产总值超过300万元的最早年份.‎ 算法分析：‎ 第一步， 输入 。‎ 第二步，计算 。‎ 第三步，判断 ， 若是，则输出该年的年份；否则， 。‎ 循环结构：‎ ‎（1）循环体：设a为某年的年生产总值，t为年生产总值的年增长量，n为年份，则t= ，a= ，n= 。‎ ‎（2）初始值：n= ，a= 。‎ ‎（3）控制条件：当“ ”时终止循环。‎ 程序框图：‎ ‎1、如图（1）所示程序的输出结果为s=132, 则判断中应填 .‎ A、i≥10？ B、i≥11？ ‎ C、i≤11？ D、i≥12？‎ ‎2、如图(2)程序框图箭头b指向①处时，输出 s=__________.‎ 箭头b指向②处时，输出 s=__________‎ ‎3、如图(3)是为求1~1000的所有偶数的和而设计的一个程序空白框图，将空白处补上。‎ ‎①__________。②__________。‎ 总结反思 ‎1、条件结构：是根据指定打件选择执行不同指令的控制结构。根据给定的条件P是否成立而选择执行A框或B框。无论P条件是否成立，只能执行A框或B框之一，不可能同时执行A框和B框，也不可能A框、B框都不执行。‎ ‎2．循环结构要在某个条件下终止循环，这就需要条件结构来判断。因此，循环结构中一定包含条件结构。‎ ‎ 3．在循环结构中都有一个计数变量和累加变量。计数变量用于记录循环次数，累加变量用于输出结果。计数变量和累加变量一般是同步执行的，累加一次，计数一次。‎ ‎4．画循环结构流程图前：‎ ‎①确定循环变量和初始条件；②确定算法中反复执行的部分，即循环体；‎ ‎③确定循环的转向位置； ④确定循环的终止条件.‎