2013年全国统一高考数学试卷（文科）（新课标ⅱ）

2013年全国统一高考数学试卷（文科）（新课标ⅱ）

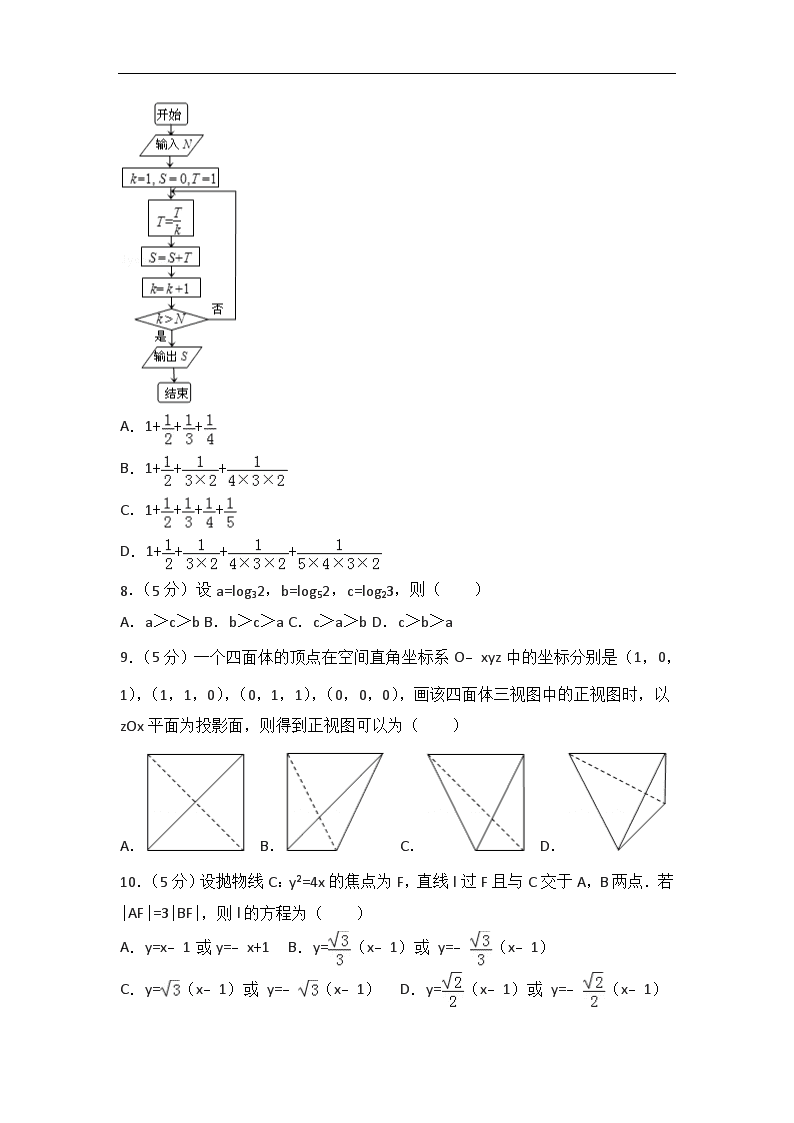
‎2013年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ ‎　‎ 一、选择题：本大题共12小题．每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的．‎ ‎1．（5分）已知集合M={x|﹣3＜x＜1，x∈R}，N={﹣3，﹣2，﹣1，0，1}，则M∩N=（　　）‎ A．{﹣2，﹣1，0，1} B．{﹣3，﹣2，﹣1，0} C．{﹣2，﹣1，0} D．{﹣3，﹣2，﹣1}‎ ‎2．（5分）=（　　）‎ A．2 B．2 C． D．1‎ ‎3．（5分）设x，y满足约束条件 ，则z=2x﹣3y的最小值是（　　）‎ A．﹣7 B．﹣6 C．﹣5 D．﹣3‎ ‎4．（5分）△ABC的内角A，B，C的对边分别为a，b，c，已知b=2，B=，C=，则△ABC的面积为（　　）‎ A．2+2 B． C．2﹣2 D．﹣1‎ ‎5．（5分）设椭圆C：=1（a＞b＞0）的左、右焦点分别为F1、F2，P是C上的点PF2⊥F1F2，∠PF1F2=30°，则C的离心率为（　　）‎ A． B． C． D．‎ ‎6．（5分）已知sin2α=，则cos2（α+）=（　　）‎ A． B． C． D．‎ ‎7．（5分）执行如图的程序框图，如果输入的N=4，那么输出的S=（　　）‎ A．1+++‎ B．1+++‎ C．1++++‎ D．1++++‎ ‎8．（5分）设a=log32，b=log52，c=log23，则（　　）‎ A．a＞c＞b B．b＞c＞a C．c＞a＞b D．c＞b＞a ‎9．（5分）一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（　　）‎ A． B． C． D．‎ ‎10．（5分）设抛物线C：y2=4x的焦点为F，直线l过F且与C交于A，B两点．若|AF|=3|BF|，则l的方程为（　　）‎ A．y=x﹣1或y=﹣x+1 B．y=（x﹣1）或 y=﹣（x﹣1）‎ C．y=（x﹣1）或 y=﹣（x﹣1） D．y=（x﹣1）或 y=﹣（x﹣1）‎ ‎11．（5分）已知函数f（x）=x3+ax2+bx+c，下列结论中错误的是（　　）‎ A．∃x0∈R，f（x0）=0‎ B．函数y=f（x）的图象是中心对称图形 C．若x0是f（x）的极小值点，则f（x ）在区间（﹣∞，x0）上单调递减 D．若x0是f（x）的极值点，则f′（x0 ）=0‎ ‎12．（5分）若存在正数x使2x（x﹣a）＜1成立，则a的取值范围是（　　）‎ A．（﹣∞，+∞） B．（﹣2，+∞） C．（0，+∞） D．（﹣1，+∞）‎ ‎　‎ 二、填空题：本大题共4小题，每小题4分．‎ ‎13．（4分）从1，2，3，4，5中任意取出两个不同的数，其和为5的概率是　 　．‎ ‎14．（4分）已知正方形ABCD的边长为2，E为CD的中点，则•=　 　．‎ ‎15．（4分）已知正四棱锥O﹣ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为　 　．‎ ‎16．（4分）函数y=cos（2x+φ）（﹣π≤φ＜π）的图象向右平移个单位后，与函数y=sin（2x+）的图象重合，则φ=　 　．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）已知等差数列{an}的公差不为零，a1=25，且a1，a11，a13成等比数列．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求a1+a4+a7+…+a3n﹣2．‎ ‎18．（12分）如图，直三棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点 ‎（Ⅰ）证明：BC1∥平面A1CD；‎ ‎（Ⅱ）AA1=AC=CB=2，AB=，求三棱锥C﹣A1DE的体积．‎ ‎19．（12分）经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以X（单位：t，100≤X≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．‎ ‎（Ⅰ）将T表示为X的函数；‎ ‎（Ⅱ）根据直方图估计利润T不少于57000元的概率．‎ ‎20．（12分）在平面直角坐标系xOy中，已知圆P在x轴上截得线段长为2，在y轴上截得线段长为2．‎ ‎（Ⅰ）求圆心P的轨迹方程；‎ ‎（Ⅱ）若P点到直线y=x的距离为，求圆P的方程．‎ ‎21．（12分）已知函数f（x）=x2e﹣x ‎（Ⅰ）求f（x）的极小值和极大值；‎ ‎（Ⅱ）当曲线y=f（x）的切线l的斜率为负数时，求l在x轴上截距的取值范围．‎ ‎　‎ 选做题．请考生在第22、23、24题中任选择一题作答，如果多做，则按所做的第一部分，作答时请写清题号．‎ ‎22．【选修4﹣1几何证明选讲】‎ 如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B、E、F、C四点共圆．‎ ‎（1）证明：CA是△ABC外接圆的直径；‎ ‎（2）若DB=BE=EA，求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值．‎ ‎23．已知动点P、Q都在曲线（β为参数）上，对应参数分别为β=α与β=2α（0＜α＜2π），M为PQ的中点．‎ ‎（1）求M的轨迹的参数方程；‎ ‎（2）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．‎ ‎24．（14分）【选修4﹣﹣5；不等式选讲】‎ 设a，b，c均为正数，且a+b+c=1，证明：‎ ‎（Ⅰ）‎ ‎（Ⅱ）．‎ ‎　‎ ‎2013年全国统一高考数学试卷（文科）（新课标Ⅱ）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题．每小题5分，在每个小题给出的四个选项中，只有一项是符合要求的．‎ ‎1．（5分）已知集合M={x|﹣3＜x＜1，x∈R}，N={﹣3，﹣2，﹣1，0，1}，则M∩N=（　　）‎ A．{﹣2，﹣1，0，1} B．{﹣3，﹣2，﹣1，0} C．{﹣2，﹣1，0} D．{﹣3，﹣2，﹣1}‎ ‎【分析】找出集合M与N的公共元素，即可求出两集合的交集．‎ ‎【解答】解：∵集合M={x|﹣3＜x＜1，x∈R}，N={﹣3，﹣2，﹣1，0，1}，‎ ‎∴M∩N={﹣2，﹣1，0}．‎ 故选：C．‎ ‎【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．‎ ‎　‎ ‎2．（5分）=（　　）‎ A．2 B．2 C． D．1‎ ‎【分析】通过复数的分子与分母同时求模即可得到结果．‎ ‎【解答】解：===．‎ 故选：C．‎ ‎【点评】本题考查复数的模的求法，考查计算能力．‎ ‎　‎ ‎3．（5分）设x，y满足约束条件 ，则z=2x﹣3y的最小值是（　　）‎ A．﹣7 B．﹣6 C．﹣5 D．﹣3‎ ‎【分析】先画出满足约束条件：，的平面区域，求出平面区域的各角点，然后将角点坐标代入目标函数，比较后，即可得到目标函数z=2x﹣3y的最小值．‎ ‎【解答】解：根据题意，画出可行域与目标函数线如下图所示，‎ 由得，‎ 由图可知目标函数在点A（3，4）取最小值z=2×3﹣3×4=﹣6．‎ 故选：B．‎ ‎【点评】用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．‎ ‎　‎ ‎4．（5分）△ABC的内角A，B，C的对边分别为a，b，c，已知b=2，B=，C=，则△ABC的面积为（　　）‎ A．2+2 B． C．2﹣2 D．﹣1‎ ‎【分析】‎ 由sinB，sinC及b的值，利用正弦定理求出c的值，再求出A的度数，由b，c及sinA的值，利用三角形的面积公式即可求出三角形ABC的面积．‎ ‎【解答】解：∵b=2，B=，C=，‎ ‎∴由正弦定理=得：c===2，A=，‎ ‎∴sinA=sin（+）=cos=，‎ 则S△ABC=bcsinA=×2×2×=+1．‎ 故选：B．‎ ‎【点评】此题考查了正弦定理，三角形的面积公式，以及两角和与差的余弦函数公式，熟练掌握正弦定理是解本题的关键．‎ ‎　‎ ‎5．（5分）设椭圆C：=1（a＞b＞0）的左、右焦点分别为F1、F2，P是C上的点PF2⊥F1F2，∠PF1F2=30°，则C的离心率为（　　）‎ A． B． C． D．‎ ‎【分析】设|PF2|=x，在直角三角形PF1F2中，依题意可求得|PF1|与|F1F2|，利用椭圆离心率的性质即可求得答案．‎ ‎【解答】解：|PF2|=x，∵PF2⊥F1F2，∠PF1F2=30°，‎ ‎∴|PF1|=2x，|F1F2|=x，‎ 又|PF1|+|PF2|=2a，|F1F2|=2c ‎∴2a=3x，2c=x，‎ ‎∴C的离心率为：e==．‎ 故选：D．‎ ‎【点评】本题考查椭圆的简单性质，求得|PF1|与|PF2|及|F1F2|是关键，考查理解与应用能力，属于中档题．‎ ‎　‎ ‎6．（5分）已知sin2α=，则cos2（α+）=（　　）‎ A． B． C． D．‎ ‎【分析】所求式子利用二倍角的余弦函数公式化简，再利用诱导公式变形，将已知等式代入计算即可求出值．‎ ‎【解答】解：∵sin2α=，‎ ‎∴cos2（α+）=[1+cos（2α+）]=（1﹣sin2α）=×（1﹣）=．‎ 故选：A．‎ ‎【点评】此题考查了二倍角的余弦函数公式，以及诱导公式的作用，熟练掌握公式是解本题的关键．‎ ‎　‎ ‎7．（5分）执行如图的程序框图，如果输入的N=4，那么输出的S=（　　）‎ A．1+++‎ B．1+++‎ C．1++++‎ D．1++++‎ ‎【分析】由程序中的变量、各语句的作用，结合流程图所给的顺序可知当条件满足时，用S+的值代替S得到新的S，并用k+1代替k，直到条件不能满足时输出最后算出的S值，由此即可得到本题答案．‎ ‎【解答】解：根据题意，可知该按以下步骤运行 第一次：S=1，‎ 第二次：S=1+，‎ 第三次：S=1++，‎ 第四次：S=1+++．‎ 此时k=5时，符合k＞N=4，输出S的值．‎ ‎∴S=1+++‎ 故选：B．‎ ‎【点评】本题主要考查了直到型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，以及表格法的运用，属于基础题．‎ ‎　‎ ‎8．（5分）设a=log32，b=log52，c=log23，则（　　）‎ A．a＞c＞b B．b＞c＞a C．c＞a＞b D．c＞b＞a ‎【分析】判断对数值的范围，然后利用换底公式比较对数式的大小即可．‎ ‎【解答】解：由题意可知：a=log32∈（0，1），b=log52∈（0，1），c=log23＞1，‎ 所以a=log32，b=log52=，‎ 所以c＞a＞b，‎ 故选：C．‎ ‎【点评】本题考查对数值的大小比较，换底公式的应用，基本知识的考查．‎ ‎　‎ ‎9．（5分）一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（　　）‎ A． B． C． D．‎ ‎【分析】由题意画出几何体的直观图，然后判断以zOx平面为投影面，则得到正视图即可．‎ ‎【解答】解：因为一个四面体的顶点在空间直角坐标系O﹣xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），几何体的直观图如图，是正方体的顶点为顶点的一个正四面体，所以以zOx平面为投影面，则得到正视图为：‎ 故选：A．‎ ‎【点评】本题考查几何体的三视图的判断，根据题意画出几何体的直观图是解题的关键，考查空间想象能力．‎ ‎　‎ ‎10．（5分）设抛物线C：y2=4x的焦点为F，直线l过F且与C交于A，B两点．若 ‎|AF|=3|BF|，则l的方程为（　　）‎ A．y=x﹣1或y=﹣x+1 B．y=（x﹣1）或 y=﹣（x﹣1）‎ C．y=（x﹣1）或 y=﹣（x﹣1） D．y=（x﹣1）或 y=﹣（x﹣1）‎ ‎【分析】根据题意，可得抛物线焦点为F（1，0），由此设直线l方程为y=k（x﹣1），与抛物线方程联解消去x，得﹣y﹣k=0．再设A（x1，y1），B（x2，y2），由根与系数的关系和|AF|=3|BF|，建立关于y1、y2和k的方程组，解之可得k值，从而得到直线l的方程．‎ ‎【解答】解：∵抛物线C方程为y2=4x，可得它的焦点为F（1，0），‎ ‎∴设直线l方程为y=k（x﹣1）‎ 由消去x，得﹣y﹣k=0‎ 设A（x1，y1），B（x2，y2），‎ 可得y1+y2=，y1y2=﹣4…（*）‎ ‎∵|AF|=3|BF|，‎ ‎∴y1+3y2=0，可得y1=﹣3y2，代入（*）得﹣2y2=且﹣3y22=﹣4，‎ 消去y2得k2=3，解之得k=‎ ‎∴直线l方程为y=（x﹣1）或y=﹣（x﹣1）‎ 故选：C．‎ ‎【点评】‎ 本题给出抛物线的焦点弦AB被焦点F分成1：3的两部分，求直线AB的方程，着重考查了抛物线的标准方程、简单几何性质和直线与圆锥曲线的位置关系等知识，属于中档题．‎ ‎　‎ ‎11．（5分）已知函数f（x）=x3+ax2+bx+c，下列结论中错误的是（　　）‎ A．∃x0∈R，f（x0）=0‎ B．函数y=f（x）的图象是中心对称图形 C．若x0是f（x）的极小值点，则f（x ）在区间（﹣∞，x0）上单调递减 D．若x0是f（x）的极值点，则f′（x0 ）=0‎ ‎【分析】对于A，对于三次函数f（x ）=x3+ax2+bx+c，由于当x→﹣∞时，y→﹣∞，当x→+∞时，y→+∞，故在区间（﹣∞，+∞）肯定存在零点；‎ 对于B，根据对称变换法则，求出对应中心坐标，可以判断；‎ 对于C：采用取特殊函数的方法，若取a=﹣1，b=﹣1，c=0，则f（x）=x3﹣x2﹣x，利用导数研究其极值和单调性进行判断；‎ D：若x0是f（x）的极值点，根据导数的意义，则f′（x0 ）=0，正确．‎ ‎【解答】解：‎ A、对于三次函数f （x ）=x3+ax2+bx+c，‎ A：由于当x→﹣∞时，y→﹣∞，当x→+∞时，y→+∞，‎ 故∃x0∈R，f（x0）=0，故A正确；‎ B、∵f（﹣﹣x）+f（x）=（﹣﹣x）3+a（﹣﹣x）2+b（﹣﹣x）+c+x3+ax2+bx+c=﹣+2c，‎ f（﹣）=（﹣）3+a（﹣）2+b（﹣）+c=﹣+c，‎ ‎∵f（﹣﹣x）+f（x）=2f（﹣），‎ ‎∴点P（﹣，f（﹣））为对称中心，故B正确．‎ C、若取a=﹣1，b=﹣1，c=0，则f（x）=x3﹣x2﹣x，‎ 对于f（x）=x3﹣x2﹣x，∵f′（x）=3x2﹣2x﹣1‎ ‎∴由f′（x）=3x2﹣2x﹣1＞0得x∈（﹣∞，﹣）∪（1，+∞）‎ 由f′（x）=3x2﹣2x﹣1＜0得x∈（﹣，1）‎ ‎∴函数f（x）的单调增区间为：（﹣∞，﹣），（1，+∞），减区间为：（﹣，1），‎ 故1是f（x）的极小值点，但f（x ）在区间（﹣∞，1）不是单调递减，故C错误；‎ D：若x0是f（x）的极值点，根据导数的意义，则f′（x0 ）=0，故D正确．‎ 由于该题选择错误的，故选：C．‎ ‎【点评】本题考查了导数在求函数极值中的应用，利用导数求函数的单调区间，及导数的运算．‎ ‎　‎ ‎12．（5分）若存在正数x使2x（x﹣a）＜1成立，则a的取值范围是（　　）‎ A．（﹣∞，+∞） B．（﹣2，+∞） C．（0，+∞） D．（﹣1，+∞）‎ ‎【分析】转化不等式为，利用x是正数，通过函数的单调性，求出a的范围即可．‎ ‎【解答】解：因为2x（x﹣a）＜1，所以，‎ 函数y=是增函数，x＞0，所以y＞﹣1，即a＞﹣1，‎ 所以a的取值范围是（﹣1，+∞）．‎ 故选：D．‎ ‎【点评】本题考查不等式的解法，函数单调性的应用，考查分析问题解决问题的能力．‎ ‎　‎ 二、填空题：本大题共4小题，每小题4分．‎ ‎13．（4分）从1，2，3，4，5中任意取出两个不同的数，其和为5的概率是　0.2　．‎ ‎【分析】由题意结合组合数公式可得总的基本事件数，再找出和为5的情形，由古典概型的概率公式可得答案．‎ ‎【解答】解：从1，2，3，4，5中任意取出两个不同的数共有=10种情况，‎ 和为5的有（1，4）（2，3）两种情况，‎ 故所求的概率为：=0.2‎ 故答案为：0.2‎ ‎【点评】本题考查古典概型及其概率公式，属基础题．‎ ‎　‎ ‎14．（4分）已知正方形ABCD的边长为2，E为CD的中点，则•=　2　．‎ ‎【分析】根据两个向量的加减法的法则，以及其几何意义，可得要求的式子为（）•（），再根据两个向量垂直的性质，运算求得结果．‎ ‎【解答】解：∵已知正方形ABCD的边长为2，E为CD的中点，则 =0，‎ 故 =（ ）•（）=（）•（）=﹣+﹣=4+0﹣0﹣=2，‎ 故答案为 2．‎ ‎【点评】本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量垂直的性质，属于中档题．‎ ‎　‎ ‎15．（4分）已知正四棱锥O﹣ABCD的体积为，底面边长为，则以O为球心，OA为半径的球的表面积为　24π　．‎ ‎【分析】‎ 先直接利用锥体的体积公式即可求得正四棱锥O﹣ABCD的高，再利用直角三角形求出正四棱锥O﹣ABCD的侧棱长OA，最后根据球的表面积公式计算即得．‎ ‎【解答】解：如图，正四棱锥O﹣ABCD的体积V=sh=（×）×OH=，‎ ‎∴OH=，‎ 在直角三角形OAH中，OA===‎ 所以表面积为4πr2=24π；‎ 故答案为：24π．‎ ‎【点评】本题考查锥体的体积、球的表面积计算，考查学生的运算能力，属基础题．‎ ‎　‎ ‎16．（4分）函数y=cos（2x+φ）（﹣π≤φ＜π）的图象向右平移个单位后，与函数y=sin（2x+）的图象重合，则φ=　　．‎ ‎【分析】根据函数图象平移的公式，可得平移后的图象为y=cos[2（x﹣）+φ]的图象，即y=cos（2x+φ﹣π）的图象．结合题意得函数y=sin（2x+）=的图象与y=cos（2x+φ﹣π）图象重合，由此结合三角函数的诱导公式即可算出φ的值．‎ ‎【解答】解：函数y=cos（2x+φ）（﹣π≤φ＜π）的图象向右平移 个单位后，得平移后的图象的函数解析式为 y=cos[2（x﹣）+φ]=cos（2x+φ﹣π），‎ 而函数y=sin（2x+）=，‎ 由函数y=cos（2x+φ）（﹣π≤φ＜π）的图象向右平移 个单位后，与函数y=sin（2x+）的图象重合，得 ‎2x+φ﹣π=，解得：φ=．‎ 符合﹣π≤φ＜π．‎ 故答案为．‎ ‎【点评】本题给出函数y=cos（2x+φ）的图象平移，求参数φ的值．着重考查了函数图象平移的公式、三角函数的诱导公式和函数y=Asin（ωx+φ）的图象变换等知识，属于基础题．‎ ‎　‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（12分）已知等差数列{an}的公差不为零，a1=25，且a1，a11，a13成等比数列．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求a1+a4+a7+…+a3n﹣2．‎ ‎【分析】（I）设等差数列{an}的公差为d≠0，利用成等比数列的定义可得，，再利用等差数列的通项公式可得，化为d（2a1+25d）=0，解出d即可得到通项公式an；‎ ‎（II）由（I）可得a3n﹣2=﹣2（3n﹣2）+27=﹣6n+31，可知此数列是以25为首项，﹣6为公差的等差数列．利用等差数列的前n项和公式即可得出a1+a4+a7+…+a3n﹣2．‎ ‎【解答】解：（I）设等差数列{an}的公差为d≠0，‎ 由题意a1，a11，a13成等比数列，∴，‎ ‎∴，化为d（2a1+25d）=0，‎ ‎∵d≠0，∴2×25+25d=0，解得d=﹣2．‎ ‎∴an=25+（n﹣1）×（﹣2）=﹣2n+27．‎ ‎（II）由（I）可得a3n﹣2=﹣2（3n﹣2）+27=﹣6n+31，可知此数列是以25为首项，﹣6为公差的等差数列．‎ ‎∴Sn=a1+a4+a7+…+a3n﹣2=‎ ‎=‎ ‎=﹣3n2+28n．‎ ‎【点评】熟练掌握等差数列与等比数列的通项公式及其前n项和公式是解题的关键．‎ ‎　‎ ‎18．（12分）如图，直三棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点 ‎（Ⅰ）证明：BC1∥平面A1CD；‎ ‎（Ⅱ）AA1=AC=CB=2，AB=，求三棱锥C﹣A1DE的体积．‎ ‎【分析】（Ⅰ）连接AC1 交A1C于点F，则DF为三角形ABC1的中位线，故DF∥BC1．再根据直线和平面平行的判定定理证得 BC1∥平面A1CD．‎ ‎（Ⅱ）由题意可得此直三棱柱的底面ABC为等腰直角三角形，由D为AB的中点可得CD⊥平面ABB1A1．求得CD的值，利用 勾股定理求得A1D、DE和A1E的值，可得A1D⊥DE．进而求得的值，再根据三棱锥C﹣A1DE的体积 为••CD，运算求得结果．‎ ‎【解答】解：（Ⅰ）证明：连接AC1 交A1C于点F，则F为AC1的中点．‎ ‎∵直棱柱ABC﹣A1B1C1中，D，E分别是AB，BB1的中点，故DF为三角形ABC1的中位线，故DF∥BC1．‎ 由于DF⊂平面A1CD，而BC1不在平面A1CD中，故有BC1∥平面A1CD．‎ ‎（Ⅱ）∵AA1=AC=CB=2，AB=2，故此直三棱柱的底面ABC为等腰直角三角形．‎ 由D为AB的中点可得CD⊥平面ABB1A1 ，∴CD==．‎ ‎∵A1D==，同理，利用勾股定理求得 DE=，A1E=3．‎ 再由勾股定理可得+DE2=，∴A1D⊥DE．‎ ‎∴==，‎ ‎∴=••CD=1．‎ ‎【点评】本题主要考查直线和平面平行的判定定理的应用，求三棱锥的体积，体现了数形结合的数学思想，属于中档题．‎ ‎　‎ ‎19．（12分）经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以X（单位：t，100≤X≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．‎ ‎（Ⅰ）将T表示为X的函数；‎ ‎（Ⅱ）根据直方图估计利润T不少于57000元的概率．‎ ‎【分析】（I）由题意先分段写出，当X∈[100，130）时，当X∈[130，150）时，和利润值，最后利用分段函数的形式进行综合即可．‎ ‎（II）由（I）知，利润T不少于57000元，当且仅当120≤X≤150．再由直方图知需求量X∈[120，150]的频率为0.7，利用样本估计总体的方法得出下一个销售季度的利润T不少于57000元的概率的估计值．‎ ‎【解答】解：（I）由题意得，当X∈[100，130）时，T=500X﹣300（130﹣X）=800X﹣39000，‎ 当X∈[130，150]时，T=500×130=65000，‎ ‎∴T=．‎ ‎（II）由（I）知，利润T不少于57000元，当且仅当120≤X≤150．‎ 由直方图知需求量X∈[120，150]的频率为0.7，‎ 所以下一个销售季度的利润T不少于57000元的概率的估计值为0.7．‎ ‎【点评】本题考查用样本的频率分布估计总体分布及识图的能力，求解的重点是对题设条件及直方图的理解，了解直方图中每个小矩形的面积的意义．‎ ‎　‎ ‎20．（12分）在平面直角坐标系xOy中，已知圆P在x轴上截得线段长为2，在y轴上截得线段长为2．‎ ‎（Ⅰ）求圆心P的轨迹方程；‎ ‎（Ⅱ）若P点到直线y=x的距离为，求圆P的方程．‎ ‎【分析】（Ⅰ）由题意，可直接在弦心距、弦的一半及半径三者组成的直角三角形中利用勾股定理建立关于点P的横纵坐标的方程，整理即可得到所求的轨迹方程；‎ ‎（Ⅱ）由题，可先由点到直线的距离公式建立关于点P的横纵坐标的方程，将此方程与（I）所求的轨迹方程联立，解出点P的坐标，进而解出圆的半径即可写出圆P的方程．‎ ‎【解答】解：（Ⅰ）设圆心P（x，y），由题意得圆心到x轴的距离与半径之间的关系为2=﹣y2+r2，同理圆心到y轴的距离与半径之间的关系为3=﹣x2+r2，由两式整理得x2+3=y2+2，整理得y2﹣x2=1即为圆心P的轨迹方程，此轨迹是等轴双曲线 ‎（Ⅱ）由P点到直线y=x的距离为得，=，即|x﹣y|=1，即x=y+1或y=x+1，分别代入y2﹣x2=1解得P（0，﹣1）或P（0，1）‎ 若P（0，﹣1），此时点P在y轴上，故半径为，所以圆P的方程为（y+1）2+x2=3；‎ 若P（0，1），此时点P在y轴上，故半径为，所以圆P的方程为（y﹣1）2+x2=3；‎ 综上，圆P的方程为（y+1）2+x2=3或（y﹣1）2+x2=3‎ ‎【点评】本题考查求轨迹方程的方法解析法及点的直线的距离公式、圆的标准方程与圆的性质，解题的关键是理解圆的几何特征，将几何特征转化为方程 ‎　‎ ‎21．（12分）已知函数f（x）=x2e﹣x ‎（Ⅰ）求f（x）的极小值和极大值；‎ ‎（Ⅱ）当曲线y=f（x）的切线l的斜率为负数时，求l在x轴上截距的取值范围．‎ ‎【分析】‎ ‎（Ⅰ）利用导数的运算法则即可得出f′（x），利用导数与函数单调性的关系及函数的极值点的定义，即可求出函数的极值；‎ ‎（Ⅱ）利用导数的几何意义即可得到切线的斜率，得出切线的方程，利用方程求出与x轴交点的横坐标，再利用导数研究函数的单调性、极值、最值即可．‎ ‎【解答】解：（Ⅰ）∵f（x）=x2e﹣x，‎ ‎∴f′（x）=2xe﹣x﹣x2e﹣x=e﹣x（2x﹣x2），‎ 令f′（x）=0，解得x=0或x=2，‎ 令f′（x）＞0，可解得0＜x＜2；‎ 令f′（x）＜0，可解得x＜0或x＞2，‎ 故函数在区间（﹣∞，0）与（2，+∞）上是减函数，在区间（0，2）上是增函数．‎ ‎∴x=0是极小值点，x=2极大值点，又f（0）=0，f（2）=．‎ 故f（x）的极小值和极大值分别为0，．‎ ‎（Ⅱ）设切点为（），‎ 则切线方程为y﹣=（x﹣x0），‎ 令y=0，解得x==，‎ ‎∵曲线y=f（x）的切线l的斜率为负数，‎ ‎∴（＜0，‎ ‎∴x0＜0或x0＞2，‎ 令，‎ 则=．‎ ‎①当x0＜0时，0，即f′（x0）＞0，∴f（x0）在（﹣∞，0）上单调递增，∴f（x0）＜f（0）=0；‎ ‎②当x0＞2时，令f′（x0）=0，解得．‎ 当时，f′（x0）＞0，函数f（x0）单调递增；当时，f′（x0）＜0，函数f（x0）单调递减．‎ 故当时，函数f（x0）取得极小值，也即最小值，且=．‎ 综上可知：切线l在x轴上截距的取值范围是（﹣∞，0）∪．‎ ‎【点评】本题考查利用导数求函数的极值与利用导数研究函数的单调性、切线、函数的值域，综合性强，考查了推理能力和计算能力．‎ ‎　‎ 选做题．请考生在第22、23、24题中任选择一题作答，如果多做，则按所做的第一部分，作答时请写清题号．‎ ‎22．【选修4﹣1几何证明选讲】‎ 如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B、E、F、C四点共圆．‎ ‎（1）证明：CA是△ABC外接圆的直径；‎ ‎（2）若DB=BE=EA，求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值．‎ ‎【分析】（1）已知CD为△ABC外接圆的切线，利用弦切角定理可得∠DCB=∠A，及BC•AE=DC•AF，可知△CDB∽△AEF，于是∠CBD=∠AFE．‎ 利用B、E、F、C四点共圆，可得∠CFE=∠DBC，进而得到∠CFE=∠AFE=90°即可证明CA是△ABC外接圆的直径；‎ ‎（2）要求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值．只需求出其外接圆的直径的平方之比即可．由过B、E、F、C四点的圆的直径为CE，及DB=BE，可得CE=DC，利用切割线定理可得DC2=DB•DA，CA2=CB2+BA2，都用DB表示即可．‎ ‎【解答】（1）证明：∵CD为△ABC外接圆的切线，∴∠DCB=∠A，‎ ‎∵BC•AE=DC•AF，∴．‎ ‎∴△CDB∽△AEF，∴∠CBD=∠AFE．‎ ‎∵B、E、F、C四点共圆，∴∠CFE=∠DBC，∴∠CFE=∠AFE=90°．‎ ‎∴∠CBA=90°，∴CA是△ABC外接圆的直径；‎ ‎（2）连接CE，∵∠CBE=90°，‎ ‎∴过B、E、F、C四点的圆的直径为CE，由DB=BE，得CE=DC，‎ 又BC2=DB•BA=2DB2，‎ ‎∴CA2=4DB2+BC2=6DB2．‎ 而DC2=DB•DA=3DB2，‎ 故过B、E、F、C四点的圆的面积与△ABC面积的外接圆的面积比值==．‎ ‎【点评】熟练掌握弦切角定理、相似三角形的判定与性质、四点共圆的性质、直径的判定、切割线定理、勾股定理等腰三角形的性质是解题的关键．‎ ‎　‎ ‎23．已知动点P、Q都在曲线（β为参数）上，对应参数分别为β=α与β=2α（0＜α＜2π），M为PQ的中点．‎ ‎（1）求M的轨迹的参数方程；‎ ‎（2）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．‎ ‎【分析】（1）利用参数方程与中点坐标公式即可得出；‎ ‎（2）利用两点之间的距离公式、三角函数的单调性即可得出．‎ ‎【解答】解：（1）依题意有P（2cosα，2sinα），Q（2cos2α，2sin2α），‎ 因此M（cosα+cos2α，sinα+sin2α）．‎ M的轨迹的参数方程为为参数，0＜α＜2π）．‎ ‎（2）M点到坐标原点的距离d=（0＜α＜2π）．‎ 当α=π时，d=0，故M的轨迹过坐标原点．‎ ‎【点评】本题考查了参数方程与中点坐标公式、两点之间的距离公式、三角函数的单调性，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎24．（14分）【选修4﹣﹣5；不等式选讲】‎ 设a，b，c均为正数，且a+b+c=1，证明：‎ ‎（Ⅰ）‎ ‎（Ⅱ）．‎ ‎【分析】（Ⅰ）依题意，由a+b+c=1⇒（a+b+c）2=1⇒a2+b2+c2+2ab+2bc+2ca=1，利用基本不等式可得3（ab+bc+ca）≤1，从而得证；‎ ‎（Ⅱ）利用基本不等式可证得：+b≥2a，+c≥2b，+a≥2c，三式累加即可证得结论．‎ ‎【解答】证明：（Ⅰ）由a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca得：‎ a2+b2+c2≥ab+bc+ca，‎ 由题设得（a+b+c）2=1，即a2+b2+c2+2ab+2bc+2ca=1，‎ 所以3（ab+bc+ca）≤1，即ab+bc+ca≤．‎ ‎（Ⅱ）因为+b≥2a，+c≥2b，+a≥2c，‎ 故+++（a+b+c）≥2（a+b+c），即++≥a+b+c．‎ 所以++≥1．‎ ‎【点评】本题考查不等式的证明，突出考查基本不等式与综合法的应用，考查推理论证能力，属于中档题．‎ ‎　‎