高中数学必修1教案：第九章直线平面简单几何体(B)(第5课)空间的平行直线与异面直线(2)

高中数学必修1教案：第九章直线平面简单几何体(B)(第5课)空间的平行直线与异面直线(2)

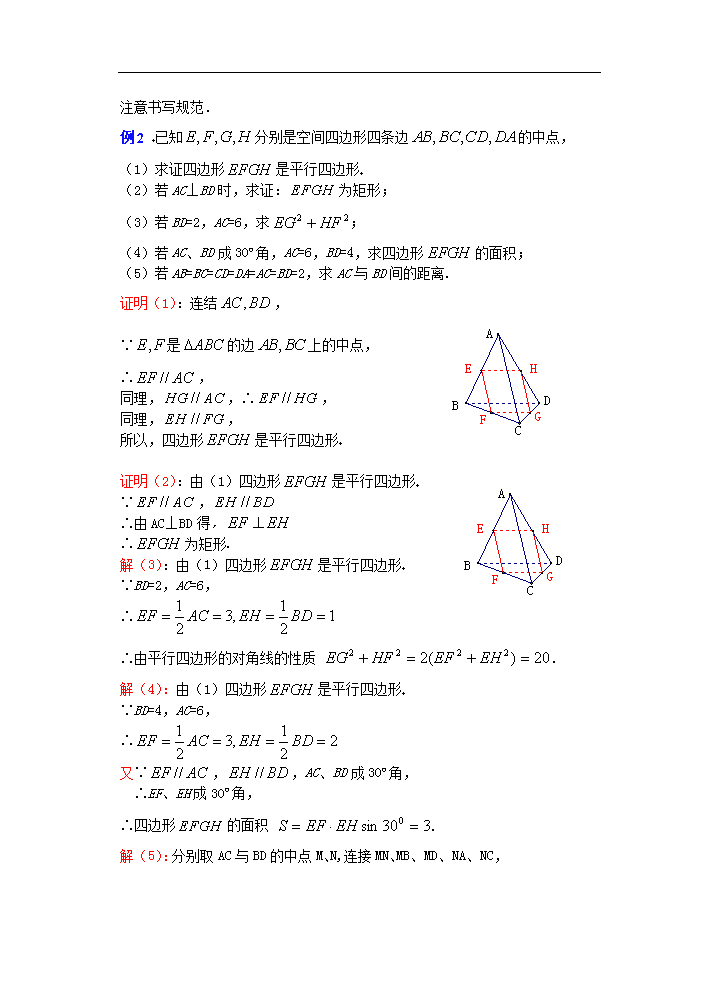
课 题：9．2空间的平行直线与异面直线(二) ‎ 教学目的：‎ ‎1. 掌握两异面直线的公垂线和距离的概念；‎ ‎2. 掌握两异面直线所成角及距离的求法．‎ ‎3. 能求出一些较特殊的异面直线的距离 教学重点：两异面直线的公垂线及距离的概念.‎ 教学难点：两异面直线所成角及距离的求法.‎ 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、复习引入： ‎ ‎1 空间两直线的位置关系 ‎（1）相交——有且只有一个公共点；‎ ‎（2）平行——在同一平面内，没有公共点；‎ ‎（3）异面——不在任何一个平面内，没有公共点；‎ ‎2.公理4 ：平行于同一条直线的两条直线互相平行 推理模式：．‎ ‎3.等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等 ‎4.等角定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.‎ ‎5.空间两条异面直线的画法 ‎6．异面直线定理：连结平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线 推理模式：与是异面直线 ‎7．异面直线所成的角：已知两条异面直线，经过空间任一点作直线，所成的角的大小与点 的选择无关，把所成的锐角（或直角）叫异面直线所成的角（或夹角）．为了简便，点通常取在异面直线的一条上异面直线所成的角的范围：‎ ‎8．异面直线垂直：如果两条异面直线所成的角是直角，则叫两条异面直线垂直．两条异面直线 垂直，记作．‎ ‎9．求异面直线所成的角的方法：‎ ‎（1）通过平移，在一条直线上找一点，过该点做另一直线的平行线；‎ ‎（2）找出与一条直线平行且与另一条相交的直线，那么这两条相交直线所成的角即为所求 二、讲解新课：‎ 两条异面直线的公垂线、距离 和两条异面直线都垂直相交的直线，我们称之为异面直线的公垂线 理解：因为两条异面直线互相垂直时，它们不一定相交，所以公垂线的定义要注意“相交”的含义．‎ 定义：两条异面直线的公垂线在这两条异面直线间的线段（公垂线段）的长度，叫做两条异面直线间的距离．‎ 两条异面直线的公垂线有且只有一条 三、讲解范例：‎ 例1 设图中的正方体的棱长为a ‎（1）图中哪些棱所在的直线与直线BA1成异面直线？‎ ‎（2）求直线BA1和CC1所成的角的大小．‎ ‎（3）求异面直线BC和AA1的距离．‎ 解：（l）∵A1不在平面BC1，而点B和直线CC1都在平面BC1内，且BCC1.‎ ‎∴直线BA1与CC1是异面直线．‎ 同理，直线C1D1、D1D、DC、AD、B‎1C1都和直线BA1成异面直线．‎ ‎（2）∵CC1∥BB1‎ ‎∴BA1和BB1所成的锐角就是BA1和CC1所成的角．‎ ‎∵∠A1BB1=45°，‎ ‎∴BA1和CC1所成的角是45°．‎ ‎（3）∵AB⊥AA1，AB∩AA1=A，‎ 又∵AB⊥BC，AB∩BC=B，‎ ‎∴AB是BC和AA1的公垂线段．‎ ‎∵AB=a，‎ ‎∴BC和AA1的距离是a．‎ 说明：本题是判定异面直线，求异面直线所成角与距离的综合题，解题时要注意书写规范．‎ 例2 已知分别是空间四边形四条边的中点，‎ ‎（1）求证四边形是平行四边形 ‎（2）若AC⊥BD时，求证：为矩形；‎ ‎（3）若BD=2，AC=6，求；‎ ‎（4）若AC、BD成30º角，AC=6，BD=4，求四边形的面积；‎ ‎（5）若AB=BC=CD=DA=AC=BD=2，求AC与BD间的距离.‎ 证明（1）：连结，‎ ‎∵是的边上的中点，‎ ‎∴，‎ 同理，，∴，‎ 同理，，‎ 所以，四边形是平行四边形 证明（2）：由（1）四边形是平行四边形 ‎∵，‎ ‎∴由AC⊥BD得，‎ ‎∴为矩形.‎ 解（3）：由（1）四边形是平行四边形 ‎∵BD=2，AC=6，‎ ‎∴‎ ‎∴由平行四边形的对角线的性质 .‎ 解（4）：由（1）四边形是平行四边形 ‎∵BD=4，AC=6，‎ ‎∴‎ 又∵，，AC、BD成30º角，‎ ‎∴EF、EH成30º角，‎ ‎∴四边形的面积 .‎ 解（5）：分别取AC与BD的中点M、N,连接MN、MB、MD、NA、NC，‎ ‎∵AB=BC=CD=DA=AC=BD=2，‎ ‎∴MB＝MD＝NA＝NC＝‎ ‎∴‎ ‎∴MN是AC与BD的公垂线段 且 ‎ ‎∴AC与BD间的距离为. ‎ 例3 平行四边形ABCD的内角C=60°,CD=2BC,沿对角线BD将平行四边形所在平面折成直二面角;求AC、BD所成的角.翰林汇 解：如图,折起前,∠A=∠C=60°,AD=BC=a,AB=DC=‎2a.‎ 由余弦定理得BD2=a2＋‎4a2－a·‎2a=‎3a2,‎ ‎∴BD=.‎ ‎∵AD2＋BD2=AB2, ∴△ABD是直角三角形.‎ 即∠ADB=90°.同理∠DBC=90°.‎ 折起后∠ADB=∠CBD=90°.‎ 如图,过A作AEBD,连结AC、CE、BE,四边形AEBD是矩形,BD⊥BE,DB⊥BC.‎ ‎∴∠CBE是二面角A—BD—C的平面角.‎ ‎∴∠CBE=90°,EC2=‎2a2.‎ ‎∵DB⊥平面EBC,∴DB⊥EC.‎ ‎∵AE⊥EC,AC2=AE2＋EC2=‎5a2,‎ 由AE‖BD得∠CAE，即为AC与BD所成的角.‎ 在Rt△AEC中,cos∠CAE=.‎ 于是AC与BD所成角为arccos.翰林汇 例4 空间四边形中，，分别是的中点，，求异面直线所成的角 解：取中点，连结，∵分别是的中点，‎ ‎∴且，‎ ‎∴异面直线所成的角即为所成的角，‎ 在中，，‎ ‎∴，异面直线所成的角为．‎ 说明：异面直线所成的角是锐角或直角，当三角形内角是钝角时，表示异面直线所成的角是它的补角 例5 在正方体ABCD－A1B‎1C1D1中,求(1)A1B与B1D1所成角;(2)AC与BD1所成角.翰林汇 解(1)如图,连结BD,A1D,‎ ‎∵ABCD-A1B‎1C1D1是正方体,∴DD1平行且相等BB1.‎ ‎∴DBB1D1为平行四边形,∴BD//B1D1.‎ ‎∴A1B,BD,A1D是全等的正方形的对角线.‎ ‎∴A1B=BD=A1D,△A1BD是正三角形,‎ ‎∴∠A1BD=60o,‎ ‎∵∠A1BD是锐角,‎ ‎∴∠A1BD是异面直线A1B与B1D1所成的角.‎ ‎∴A1B与B1D1成角为60o.‎ ‎(2)连BD交AC于O,取DD1 中点E,连EO,EA,EC.‎ ‎∵O为BD中点,∴OE//BD1.‎ ‎∵∠EDA=90o=∠EDC,ED=ED,AD=DC,∴△EDA≌△EDC,∴EA=EC.‎ 在等腰△EAC中,∵O是AC的中点,∴EO⊥AC,∴∠EOA=90o.‎ 又∴∠EOA是异面直线AC与BD1所成角,∴AC与BD成角90o. 翰林汇 例6．在长方体中，已知AB=a，BC=b，=c(a＞b)，求异面直线与AC所成角的余弦值 ‎ 解：在长方体的一旁，补上一个全等的长方体，‎ 则BE≠AC，（或其补角）即和CD所的角 ‎ ∵，，，‎ ‎ ∴‎ ‎＝‎ ‎ ∴与AC所成角的余弦值为.翰林汇 四、课堂练习：‎ ‎1．判断题（对的打“√”，错的打“×”）‎ ‎ （1）垂直于两条异面直线的直线有且只有一条 （ ）‎ ‎ （2）两线段AB、CD不在同一平面内，如果AC=BD，AD=BC，则AB⊥CD（ ） ‎ ‎ （3）在正方体中，相邻两侧面的一对异面的对角线所成的角为60º （ ）‎ ‎ （4）四边形的一边不可能既和它的邻边垂直，又和它的对边垂直 （ ）‎ 答案：（1）× （2）× （3）√ （4）× ‎ E A F B C M N D ‎2．右图是正方体平面展开图，在这个正方体中 ‎①BM与ED平行；‎ ‎②CN与BE是异面直线；‎ ‎③CN与BM成60º角；‎ ‎④DM与BN垂直.‎ ‎ 以上四个命题中，正确命题的序号是 （ ）‎ ‎ （A）①②③ （B）②④ （C）③④ （D）②③④‎ 答案：C ‎3．已知空间四边形ABCD.‎ ‎(1)求证：对角线AC与BD是异面直线;‎ ‎(2)若AC⊥BD,E,F,G,H分别这四条边AB,BC,CD,DA的中点,试判断四边形EFGH的形状;‎ ‎(3)若AB＝BC＝CD＝DA,作出异面直线AC与BD的公垂线段.翰林汇 证明：(1)∵ABCD是空间四边形,‎ ‎∴A点不在平面BCD上,而C平面BCD,‎ ‎∴AC过平面BCD外一点A与平面BCD内一点C,‎ 又∵BD平面BCD,且CBD.∴AC与BD是异面直线.‎ ‎(2)解如图,∵E,F分别为AB,BC的中点,∴EF//AC,且EF=AC.‎ 同理HG//AC,且HG=AC.∴EF平行且相等HG,∴EFGH是平行四边形.‎ 又∵F,G分别为BC,CD的中点,∴FG//BD,‎ ‎∴∠EFG是异面直线AC与BD所成的角.‎ ‎∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.‎ ‎(3)作法取BD中点E,AC中点F,连EF,则EF即为所求.‎ ‎4．完成下列证明，已知直线a、b、c不共面，它们相交于点P，AÎa，DÎa，BÎb，EÎc求证：BD和AE是异面直线 证明：假设__ 共面于g，则点A、E、B、D都在平面__内 ‎ QAÎa，DÎa，∴__Ìγ.‎ QPÎa，∴PÎ__.‎ QPÎb，BÎb，PÎc，EÎc ‎ ∴__Ìg，__Ìg，这与____矛盾 ‎∴BD、AE__________‎ ‎ 翰林汇 答案：假设BD、AE共面于g，则点A、E、B、D都在平面 g 内 ‎∵AÎa，DÎa，∴ a Ìg.‎ ‎∵PÎa，PÎ g .‎ ‎∵PÎb，BÎb，PÎc，EÎc.‎ ‎∴ b Ìg，c Ìg，这与a、b、c不共面矛盾 ‎∴BD、AE是异面直线翰林 五、小结 ：本节课我们学习了两条异面直线所成的角，以及两条异面直线间的距离和有关概念．并学会如何求两条异面直线所成角及距离，懂得将其转化为平面几何问题来解决 空间四边形的中点四边形为平行四边形、矩形、菱形的条件，以及与对角线的长度夹角有关的问题的解法 ‎ 六、课后作业： ‎ 七、板书设计（略）‎ 八、课后记：‎