【数学】2021届一轮复习人教版(文理通用)第9章第1讲算法与程序框图、基本算法语句作业
对应学生用书[练案66理][练案61文]
第九章 算法初步、统计、统计案例
第一讲 算法与程序框图、基本算法语句
A组基础巩固
一、选择题
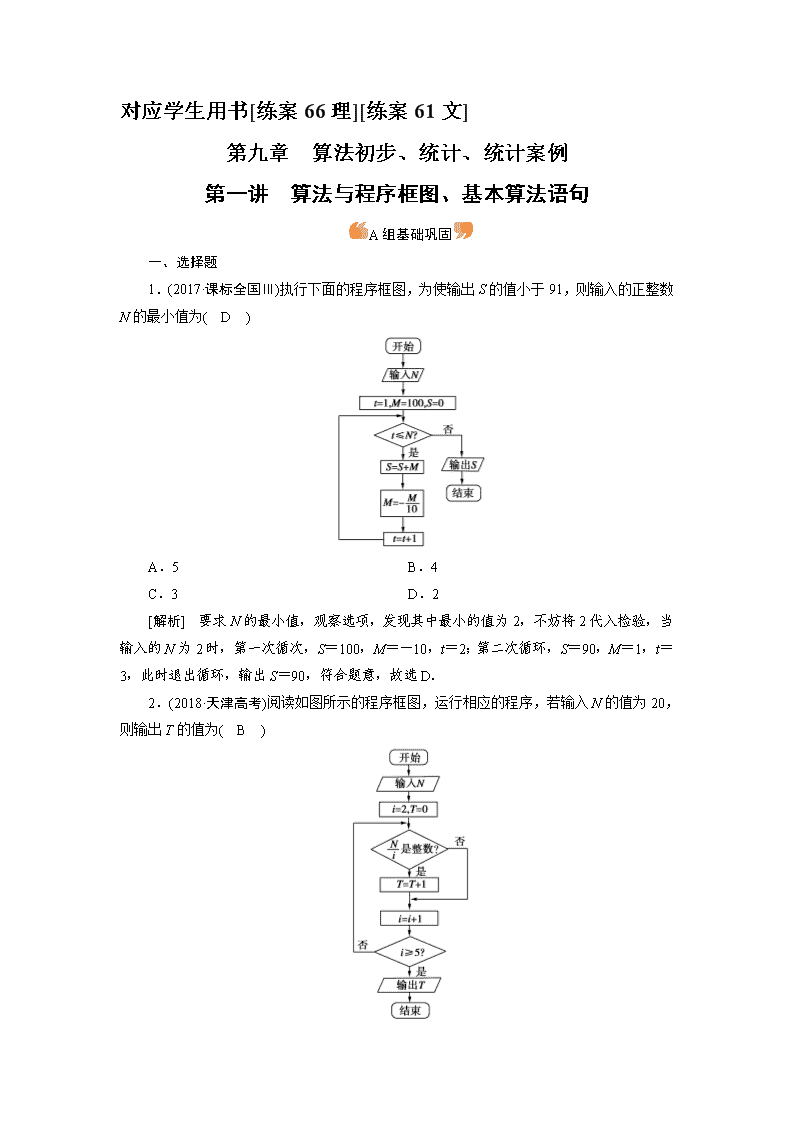
1.(2017·课标全国Ⅲ)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( D )
A.5 B.4
C.3 D.2
[解析] 要求N的最小值,观察选项,发现其中最小的值为2,不妨将2代入检验,当输入的N为2时,第一次循次,S=100,M=-10,t=2;第二次循环,S=90,M=1,t=3,此时退出循环,输出S=90,符合题意,故选D.
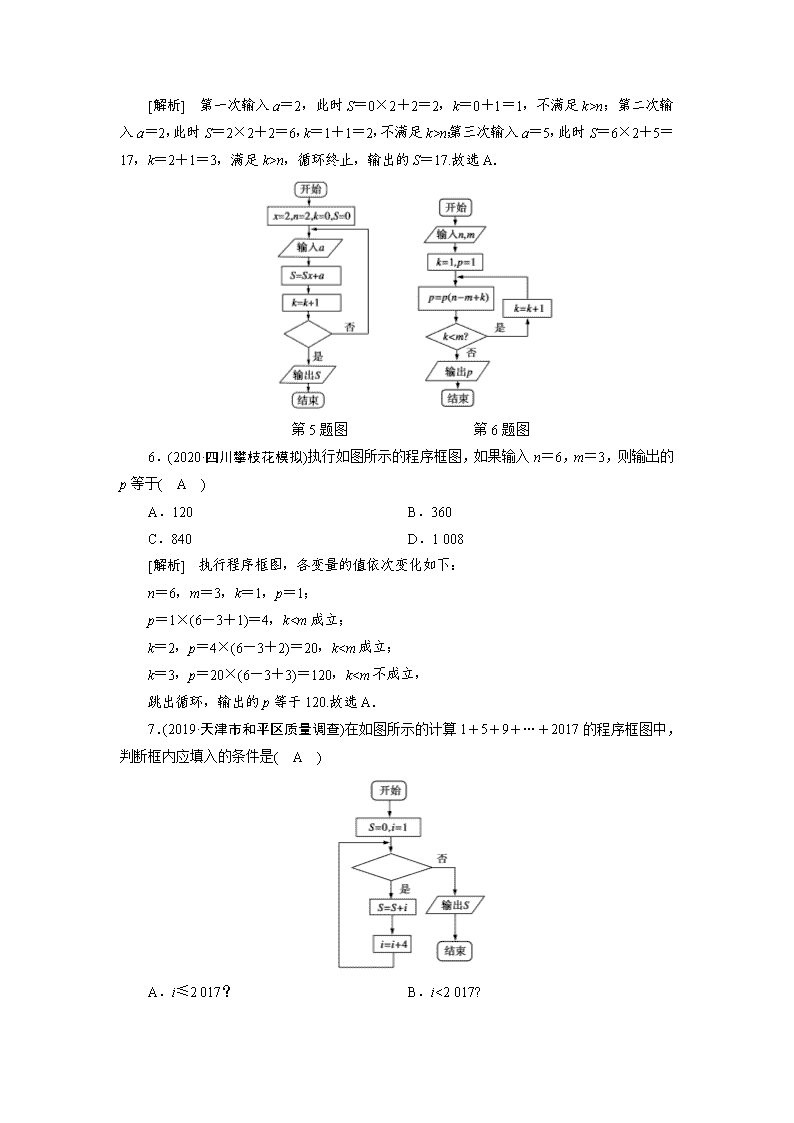
2.(2018·天津高考)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为( B )
A.1 B.2
C.3 D.4
[解析] 由程序框图知,T=1,i=3,i=4;T=2,i=5,满足条件,结束循环.故输出T的值为2.故选B.
3.(2020·云南师大附中月考)执行如图所示的程序框图,若a=0.5,b=0.9,c=log50.3,则输出的数是( B )
A.0.5 B.0.9
C.log50.3 D.0.5+0.9+log50.3
[解析] 由程序框图知,输出a,b,c中最大的数,
∵a=0.5=0.25
100,停止循环,则最后输出的x的值是231,故选D.
5.(2020·武昌调研)执行如图所示的程序框图,如果输入的a依次为2,2,5时,输出的S为17,那么在判断框中可以填入( A )
A.k>n? B.kn
;第二次输入a=2,此时S=2×2+2=6,k=1+1=2,不满足k>n;第三次输入a=5,此时S=6×2+5=17,k=2+1=3,满足k>n,循环终止,输出的S=17.故选A.
第5题图 第6题图
6.(2020·四川攀枝花模拟)执行如图所示的程序框图,如果输入n=6,m=3,则输出的p等于( A )
A.120 B.360
C.840 D.1 008
[解析] 执行程序框图,各变量的值依次变化如下:
n=6,m=3,k=1,p=1;
p=1×(6-3+1)=4,k3.10,结束,输出24.故选A.
9.(2020·广西柳州铁路一中、玉林一中联考)阅读下面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( C )
A.0 B.1
C.2 D.3
[分析] 根据给定的程序框图,逐次循环计算,即可求解,得到答案.
[解析] 由题意,第一循环:N=24,能被3整除,
N==8≤3不成立,
第二循环:N=8,不能被3整除,
N=8-1=7,N=7≤3不成立,
第三循环:N=7,不能被3整除,
N=7-1=6,N==2≤3成立,
终止循环,输出N=2,故选C.
10.(2019·四川省泸州市诊断)某班共有50名学生,其数学科学业水平考试成绩记作ai(i=1,2,3,…,50),若成绩不低于60分为合格,则如图所示的程序框图的功能是( D )
A.求该班学生数学科学业水平考试的不合格人数
B.求该班学生数学科学业水平考试的不合格率
C.求该班学生数学科学业水平考试的合格人数
D.求该班学生数学科学业水平考试的合格率
[解析] 执行程序框图,可知其功能为输入50个学生成绩ai,k表示该班学生数学科成绩合格的人数,i表示全班总人数,输出的为该班学生数学科学业水平考试的合格率,故选D.
二、填空题
11.(2020·广州市五校联考)如图所示的程序框图,其输出结果为 .
[解析] 由程序框图,得S=++…+
=[(1-)+(-)+…+(-)]
=[1+--]=,故输出的结果为.
第11题图 第12题图
12.(2019·北京市人大附中信息卷)执行如图所示的程序框图,若输入x值满足-24不成立,继续循环,x=x+1=4;执行第四次,S=S+=5,x=4≥4成立,输出S=5.
B组能力提升
1.(2019·甘肃兰州二诊)“欧几里得算法”是有记载的最古老的算法,也叫做辗转相除法,可追溯至公元前300年前,如图的程序框的算法思路就是来源于“欧几里得算法”,用于计算两个整数a,b的最大公约数执行该程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为1764,840,则输出的a=( B )
A.168 B.84
C.42 D.21
[解析] 输入的a=1 764,b=840,则c=84,不满足循环条件;a=840,b=84,则c=0满足循环条件,则最大公约数是84.故选B.
2.(2019·东北师大附中、重庆一中、吉大附中等模拟)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中.提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如右图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为5,2,则输出v的值为( B )
A.64 B.68
C.72 D.133
[解析] v=4,m=1,n=4;v=9,m=0,n=3;v=18,m=-1,n=2;v=35,m=-2,n=1;v=68,m=-3,n=0;结束循环,输出v=68,故选B.
3.
(2020·贵州模拟)执行如图所示的程序框图,若输出的结果为4,则输入的实数x的取值范围是( A )
A.[-,)
B.[-,)
C.[-2,)
D.[-,2)
[解析] 第一次循环:n=1,x=3x+1,n=2;
第二次循环:x=(3x+1)×3+1=9x+4,n=3;
第三次循环:x=(9x+4)×3+1=27x+13,
n=4,x≥12,循环结束.
可得不等式组解得-≤x<.所以若输出的结果为4,则输入的实数x的取值范围是[-,).故选A.
4.(2020·河南省洛阳市、许昌市质检)执行如图所示的程序框图,若输出的S=,则判断框内填入的条件不可以是( C )
A.k≤7? B.k<7?
C.k≥8? D.k<8?
[解析] 模拟执行程序框图,可得:S=0,k=0;
满足条件,k=2,S=;
满足条件,k=4,S=+;
满足条件,k=6,S=++,
满足条件,k=8,S=+++=;
由题意,此时应不满足条件,退出循环,输出S的值为.结合选项可得判断框内填入的条件可以是k<8.所以不可以的是k≥8的所有k.故选C.
5.如图是某县参加2018年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)在[150,155]内的学生人数).如图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图.现要统计身高在160~
180 cm(含160 cm,不含180 cm)的学生人数,则在流程图中的判断框内应填写( C )
A.i<6? B.i<7?
C.i<8? D.i<9?
[解析] 统计身高在160~180 cm的学生人数,即求A4+A5+A6+A7的值.当4≤i≤7时,符合要求.