2019高考数学（理）冲刺大题提分（讲义+练习）大题精做7 立体几何：建系困难问题（理）

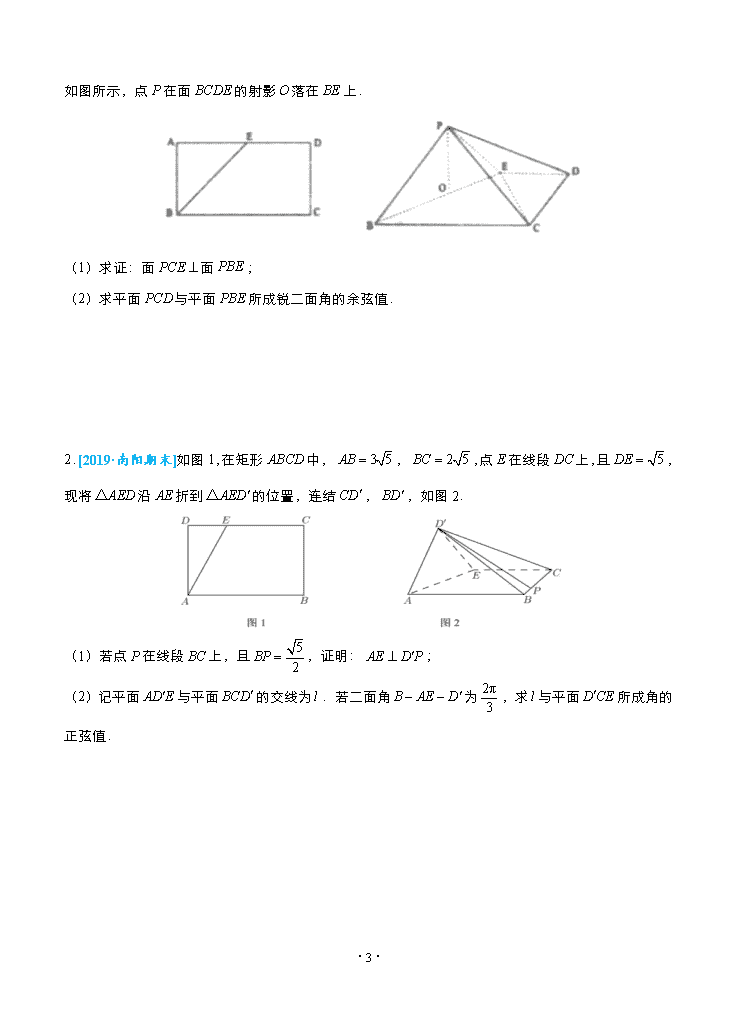
2019高考数学（理）冲刺大题提分（讲义+练习）大题精做7 立体几何：建系困难问题（理）

立体几何：建系困难问题 大题精做二 数列 大题精做七 精选大题 ‎[2019·长沙统测]已知三棱锥（如图一）的平面展开图（如图二）中，四边形为边长等于的正方形，和均为正三角形，在三棱锥中：‎ ‎（1）证明：平面平面；‎ ‎（2）若点在棱上运动，当直线与平面所成的角最大时，求二面角的余弦值．‎ ‎ ‎ 图一 图二 ‎【答案】（1）见解析；（2）．‎ ‎【解析】（1）设的中点为，连接，．‎ 由题意，得，， ．‎ ‎∵在中，，为的中点，∴，‎ ‎∵在中，，，，，∴．‎ ‎∵，，平面，∴平面，‎ ‎·7·‎ ‎∵平面，∴平面平面．‎ ‎（2）由（1）知，，，平面，‎ ‎∴是直线与平面所成的角，且，‎ ‎∴当最短时，即是的中点时，最大．‎ 由平面，，∴，，‎ 于是以，，所在直线分别为轴，轴，轴建立如图示空间直角坐标系，‎ 则，，，，，，‎ ‎，，．‎ 设平面的法向量为，‎ 则由得：．令，得，，即．‎ 设平面的法向量为，‎ 由得：，令，得，，即．‎ ‎．由图可知，二面角的余弦值为．‎ 模拟精做 ‎1．[2019·安庆期末]矩形中，，，点为中点，沿将折起至，‎ ‎·7·‎ 如图所示，点在面的射影落在上．‎ ‎（1）求证：面面；‎ ‎（2）求平面与平面所成锐二面角的余弦值．‎ ‎2．[2019·南阳期末]如图1，在矩形中，，，点在线段上，且，现将沿折到的位置，连结，，如图2．‎ ‎（1）若点在线段上，且，证明：；‎ ‎（2）记平面与平面的交线为．若二面角为，求与平面所成角的正弦值．‎ ‎·7·‎ ‎3．[2019·苏州调研]如图，在四棱锥中，已知底面是边长为1的正方形，侧面平面，，与平面所成角的正弦值为．‎ ‎（1）求侧棱的长；‎ ‎（2）设为中点，若，求二面角的余弦值．‎ 答案与解析 ‎1．【答案】（1）详见解析；（2）．‎ ‎【解析】（1）在四棱锥中，，，从而有，‎ 又∵面，而面，∴，而、面，且，‎ 由线面垂直定理可证面，又面，由面面垂直判断定定理即证面面．‎ ‎（2）由条件知面，过点做的平行线，‎ 又由（1）知面，以、、分别为、、轴建立空间直角坐标系，‎ 如图所示：‎ ‎·7·‎ ‎，，，，，‎ 面的一个法向量为，‎ 设面的法向量为，则有，‎ 从而可得面的一个法向量为，，‎ 设平面与平面所成锐二面角为，与互补，则，‎ 故平面与平面所成二面角的余弦值为．‎ ‎2．【答案】（1）详见解析；（2）．‎ ‎【解析】证明：（1）先在图1中连结，在中，由，，‎ 得，在中，由，，‎ 得，∴，则，‎ ‎∴，从而有，，即在图2中有，，‎ ‎∴平面，则；‎ ‎·7·‎ 解：（2）延长，交于点，连接，根据公理3得到直线即为，‎ 再根据二面角定义得到．在平面内过点作底面垂线，‎ 以为原点，分别为， ，及所作垂线为轴、轴、轴建立空间直角坐标系，‎ 则，，，，‎ ‎，，，‎ 设平面的一个法向量为，由，取，得．‎ ‎∴与平面所成角的正弦值为．‎ ‎3．【答案】（1）或；（2）．‎ ‎【解析】（1）取中点，中点，连结，，∵，∴，‎ 又∵平面平面，平面，平面平面，‎ ‎∴平面，∴，，‎ 又∵是正方形，∴，‎ 以为原点，，为，，轴建立空间直角坐标系（如图），‎ 则，，，，‎ 设，则，，‎ ‎·7·‎ 设平面的一个法向量为，则有，‎ 取，则，从而，‎ 设与平面所成角为，∵，‎ ‎∴，解得或，‎ ‎∴或．‎ ‎（2）由（1）知，，∴，，‎ 由（1）知，平面的一个法向量为，‎ 设平面的一个法向量为，而，，‎ ‎∴取，则，，即，‎ 设二面角的平面角为，∴，‎ 根据图形得为锐角，∴二面角的余弦值为．‎ ‎·7·‎