2018-2019学年山东省泰安四中高一上学期12月月考数学试卷

2018-2019学年山东省泰安四中高一上学期12月月考数学试卷

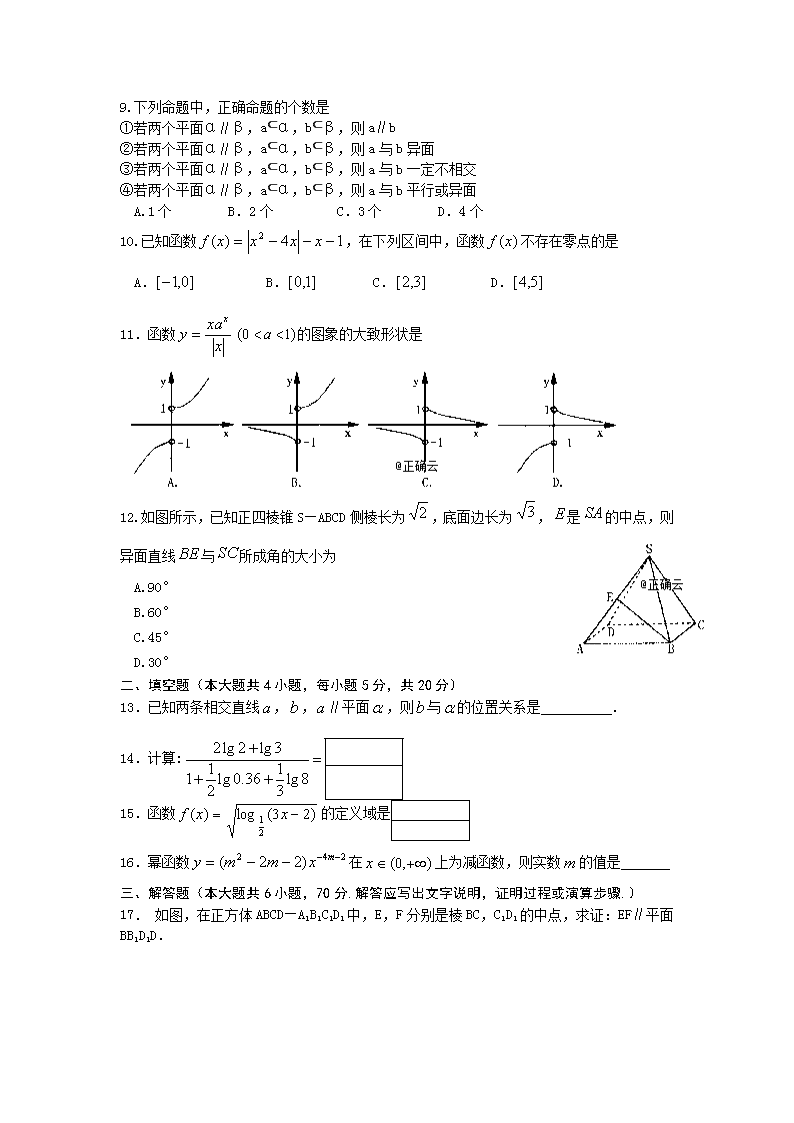
‎2018-2019学年山东省泰安四中高一上学期12月月考数学试卷 ‎2018.12‎ 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1.下列说法中正确的是 A．经过三点确定一个平面 B．两条直线确定一个平面 C．四边形确定一个平面 D．不共面的四点可以确定4个平面 ‎2．若两个球的表面积之比为1：4，则这两个球的体积之比为 A．1：2, B．1：4, C．1：8, D．1：16‎ ‎3．在正方体中，异面直线与所成的角为 A. B. C. D ‎4．如图是一平面图形的直观图，斜边，‎ 则这个平面图形的面积是 A. ‎ B．1 ‎ C． ‎ D．‎ ‎5．若圆锥的底面直径和母线都等于，则该圆锥的表面积为 A．πR 2 B．2πR 2 C．3πR 2 D．4πR 2‎ ‎6.下列函数与有相同图象的一个函数是 A． B． ‎ C． D．（）‎ ‎7．表面积是的正方体的八个顶点都在同一个球面上，则这个球的表面积是 A. B. C. D.‎ ‎8.半径为R的半圆卷成一个圆锥，圆锥的体积为 A． B. C. D.‎ ‎9.下列命题中，正确命题的个数是 ‎①若两个平面α∥β，a⊂α，b⊂β，则a∥b ‎②若两个平面α∥β，a⊂α，b⊂β，则a与b异面 ‎③若两个平面α∥β，a⊂α，b⊂β，则a与b一定不相交 ‎④若两个平面α∥β，a⊂α，b⊂β，则a与b平行或异面 A.1个 B．2个 C．3个 D．4个 ‎10.已知函数，在下列区间中，函数不存在零点的是 A． B． C． D．‎ ‎11．函数的图象的大致形状是 ‎12.如图所示，已知正四棱锥S—ABCD侧棱长为，底面边长为，是的中点，则异面直线与所成角的大小为 A.90° ‎ B.60° ‎ C.45° ‎ D.30°‎ 二、 填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．已知两条相交直线，，∥平面，则与的位置关系是 ．‎ ‎14．计算: ‎ ‎15．函数的定义域是 ‎ ‎16．幂函数在上为减函数，则实数的值是 ‎ 三、解答题（本大题共6小题，70分.解答应写出文字说明，证明过程或演算步骤.）‎ ‎17． 如图，在正方体ABCD—A1B1C1D1中，E，F分别是棱BC，C1D1的中点，求证：EF∥平面BB1D1D．‎ ‎18．如图，在正方体中，、、分别是、、的中点.求证：平面∥平面.‎ ‎19.（本小题满分12分）‎ 设函数,,‎ ‎（1）若,求取值范围; （2）求的最值，并给出最值时对应的x的值。‎ ‎20.（本小题满分12分）‎ 计算：（1）0.25×-4÷；‎ ‎（2）.‎ ‎21.如图,四棱锥PABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.‎ ‎(1)证明PA∥平面EDB; (2)证明PB⊥平面DEF.‎ ‎22.已知函数（I）判断的奇偶性；‎ ‎（Ⅱ）确定函数在上是增函数还是减函数？证明你的结论.‎ ‎（Ⅲ）若对任意都有恒成立，求的取值范围。‎ 泰安四中2018级高一12月月考 数学答案 ‎2018.12‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D C B D C D B C B D D B 一、选择题：（每小题5分，共60分）‎ 二、填空题：（每小题5分，共20分）‎ ‎13．平行或相交（直线在平面外） 14．1 15.(2/3,1] 16. 3‎ ‎17.(10分).证明：如图，取D1B1的中点O，连接OF，OB，‎ 因为OF平行且等于于，平行且等于，‎ ‎ 平行且等于，‎ 则为平行四边形，‎ ‎．‎ 平面，‎ 平面，‎ 平面 ‎18.证明:‎ ‎、分别是、的中点，‎ ‎∥‎ 又平面，平面 ‎∥平面 四边形为，∥‎ 又平面，平面 ‎∥平面，，‎ 平面∥平面 ‎19.解：（1）‎ ‎ ‎ ‎ 即 ………3分 （2） ‎∴ ………7分 ‎∴‎ 当t=2即x=4时， …………11分 故当 ‎20．（本小题满分12分）‎ 计算：（1）0.25×-4÷；‎ ‎（2）‎ ‎ ………6分 ‎（2） ………8分 ‎=‎ ‎= ………10分 ‎=2 ………12分 ‎21证明:(1)连接AC,AC交BD于O,连接EO.‎ ‎∵底面ABCD是正方形,∴点O是AC的中点,‎ 在△PAC中,EO是中位线,‎ ‎∴PA∥EO.而EO⊂平面EDB且PA⊄平面EDB,‎ ‎∴PA∥平面EDB.‎ ‎(2)∵PD⊥底面ABCD且DC⊂底面ABCD,‎ ‎∴PD⊥DC,∵PD=DC,‎ 可知△PDC是等腰直角三角形,‎ 而DE是斜边PC的中线,‎ ‎∴DE⊥PC.①‎ 同理:由PD⊥底面ABCD,得PD⊥BC.‎ ‎∵底面ABCD是正方形,有DC⊥BC,‎ ‎∴BC⊥平面PDC.而DE⊂平面PDC,‎ ‎∴BC⊥DE.②‎ 由①和②推得DE⊥平面PBC.‎ 而PB⊂平面PBC,∴DE⊥PB,‎ 又EF⊥PB且DE∩EF=E,‎ ‎∴PB⊥平面EFD.‎ ‎22.（I）因为函数为所以定义域为 ‎ ‎ 为偶函数. ‎ ‎ （Ⅱ）在区间上取 ‎ ‎ ‎ ‎ 且， 上为增函数。 ‎ ‎（Ⅲ）即可， 易得 ‎